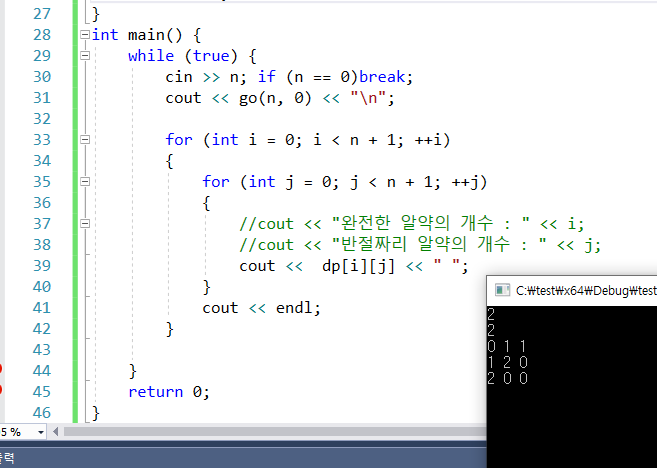
경우의 수는 더하기! 이다.
- 경우의 수
: (6,1) 은 (5,2) 일 경우와 (6,0)인 경우를 모두 포함해야 함.
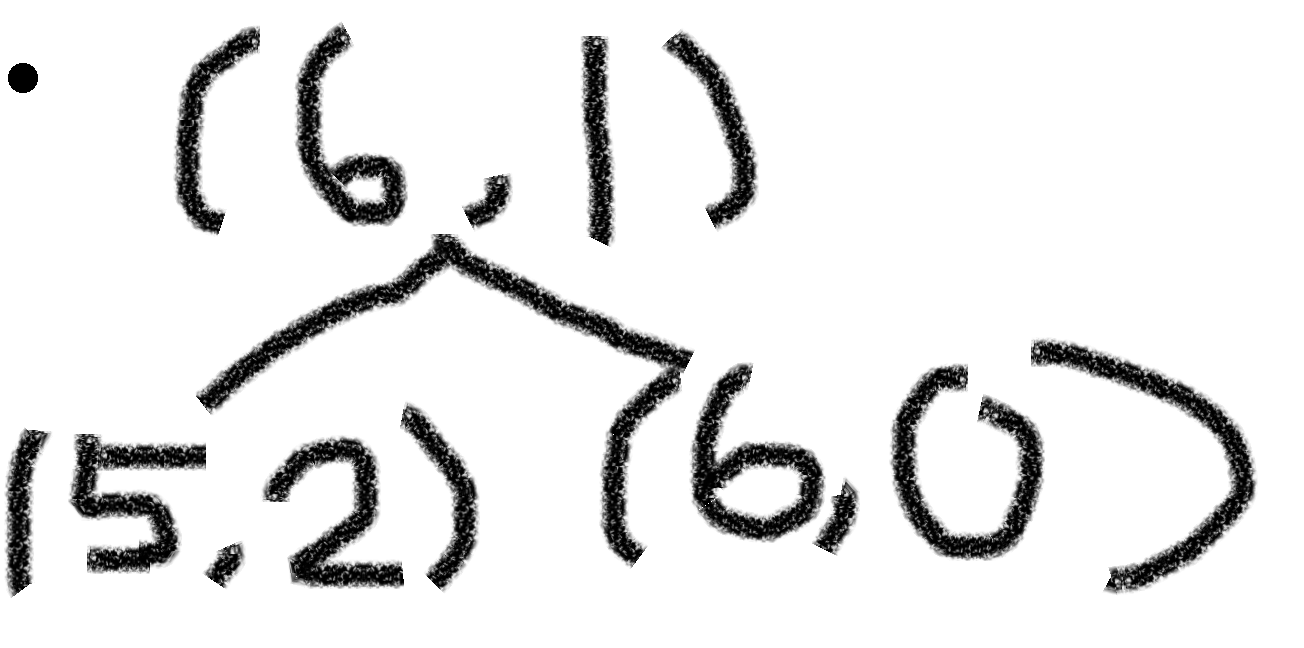
-> 이러한 상태값을 저장하기 위해서는 한개짜리와 반개짜리를
나타낼 수 있는 배열을 만들어보자
-> 그래서 나온 것이 dp[31][31]
풀이 전략
- 경우의 수가 2개가 있음.
-> 완전한 알약과 반절로 된 알약, 따라서 2차워배열로 만들 수 있음.
: 알약의 개수는 최대 30개이므로
dp[31][31] 로 만들 수 있음.
dp[한알짜리 알약][반쪽짜리 알약]
dp 설계하기
-
기저사례
: 최종 리턴 하기 -
메모이제이션
: 이미 값이 존재한다면, 그값을 리턴하자.
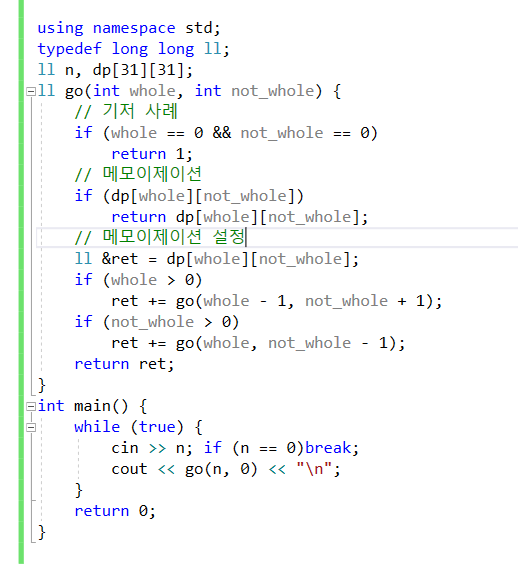
-
알약 4개로 시작했을때
: 점화식의 의미보다는 두개의 경우의 수를 어떻게 활용할 건지에 대한
코드를 만들자...
1) 맨 처음에 완전한 알약 n개와, 반절짜리 알약 0개가 들어옴.
2) 완전한 알약부터 처리를 해야함. 완전한 알약을 -1하고,
반절짜리 알약을 하나 증가 시킴.
완전한 알약 소비될때까지 진행함.
3) 반절짜리 알약을 소비해야 하므로 불완전한 알약 -1씩 감소시킴.
4) 그러다가 완전한 알약과 불완전한 알약의 갯수가 모두 0일 경우
최종적인 카운팅을 함.
생각하기
알약이 한개 일 경우, dp[1][0]
완전한 알약 하나를 먹고, 반절짜리 알약 하나를 증가함->dp[0][1]
반절짜리 알약을 하나 먹음. -> dp[0][0]
모두다 섭취 했음.
// 카운팅에 대한 부분을 기저사례에서 처리하자.
모두 다 섭취 즉, 완전한 알약과 반절짜리 알약을 모두 섭취한 경우
0 , 0일 경우에 카운팅, 1을 반환하도록 하자.
그리고 연달아서 재귀 처리한 부분에 대해서 += 연산을 함으로써,
해당 dp를 처리하자.
알약이 두개일 경우, dp[2][0]
완전한 알약이 2개 있음. dp[2][0]
완전한 알약 1개를 없애고, 반절짜리 1개 증가시킴. dp[1][1]
완전한 알약 1개를 없애고, 반절짜리 1개 증가시킴. dp[0][2]
반절짜리 알약 1개를 없애자. dp[0][1]
반절짜리 알약 1개를 없애자. dp[0][0]
완전한 알약과 반절짜리 알약의 갯수가 모두 0이므로 카운팅을 시작함.
그리고 역으로 반환 받으면서 카운팅 갯수를 누적함.