느낀점 21년 10월 4일 - for문

• 근복적으로 문제를 보자마자 어떻게 풀지 감이 안온다.
  -> 이거 일일이 노가다 해볼까? 라는 생각이 들 정도로

• 입력이 7인데 출력을 21 이 나오는 것을 통해 7을 1,2로
  일일이 잘라서 확인하기에는 어렵다. 21번 확인을 해야하므로
  -> 이러한 상황에서 진짜 딱 직관적으로 번뜩여야 한다!
  => 프로그래밍적으로 생각하면 안되.
  일단 생각해야 한다.
  예시에 있는 5가지 예시에도 꽂히면 안된다..
  작은 단위로 해볼까? 생각이 안날게 뻔하지만..

  네트워크 선이 1일 때는 1로 자를 수 있다. -> 1개
  네트워크 선이 2일 때는 1 + 1 / 2로 자를 수 있다. -> 2개
  네트워크 선이 3일 때는 1 + 1 + 1 / 1 + 2 / 2 + 1 -> 3개
  네트워크 선이 4일 때는 1 + 1 + 1 + 1 / 1 + 1 + 2 / 1 + 2 + 1 / 2 + 1 + 1
  // 2 + 2 -> 총 5개
  해보니까 규칙을 발견했다...

재귀 사용할때

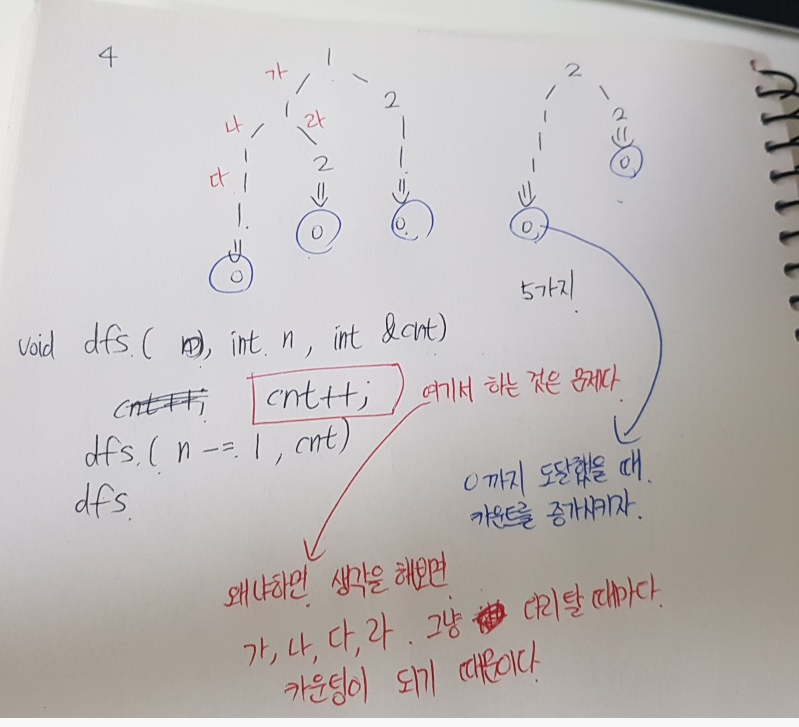
• 일단 그림을 그려보면 이렇게 된다. 전형적인 복귀하면서 카운팅 되는 dfs문제.
• 주의할 점은 어디서 카운팅을 할 것인가이다.
  그림을 보면 카운팅이 어디서 진행해야 올바른지 알 수 있다.
• 추가적으로 재귀 진행할 때 예외처리에 주의하자. 네트워크 선을 음수로 만들 수 없다는 사실에 유의하자!

풀이전략

1. 재귀 사용
   
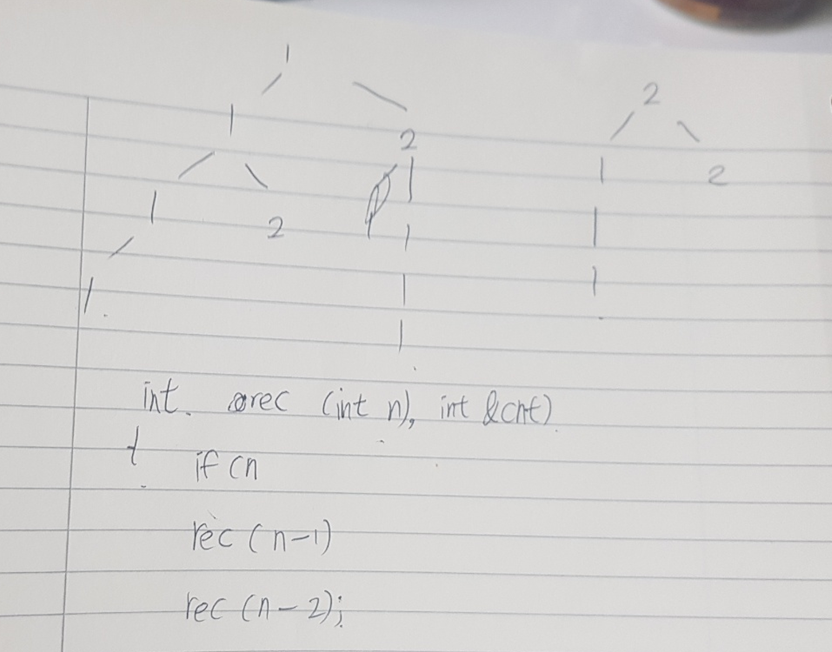
   -> 끄적여보면 재귀를 사용하면 될것 같았음.

2. dp 사용
   : 어떻게 작성해야 할지 모를때는 경우의 수를 만들어보자.
   

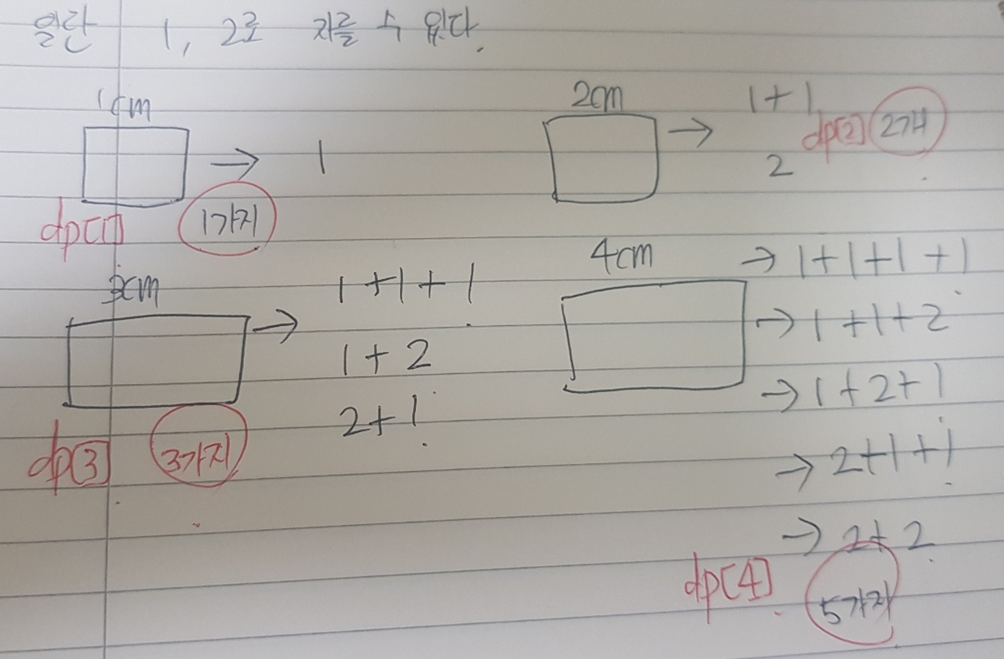
-> 점화식을 만들 수 있따.
d[3] = d[1] + d[2];
d[4] = d[3] + d[2];

소스코드

1. 재귀

void recur(int n, int&cnt)
{
	if (n == 0)
	{
		cnt++;
		return;
	}

	if(n - 1 >= 0)
		recur(n - 1, cnt);
	if (n - 2 >= 0)
		recur(n - 2, cnt);


}


int main(void)
{
	_CrtSetDbgFlag(_CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF);	
	
	int n;
	cin >> n;
	int cnt = 0;
	recur(n, cnt);
	cout << cnt;
	return 0;
}

2. dp;

int main(void)
{
	_CrtSetDbgFlag(_CRTDBG_ALLOC_MEM_DF | _CRTDBG_LEAK_CHECK_DF);	
	
	int n;
	cin >> n;
	int cnt = 0;

	vector<int>dp(n);

	dp[0] = 1;
	dp[1] = 2;
	for (int i = 2; i < n; i++)
	{
		dp[i] = dp[i - 1] + dp[i - 2];
	}

	cout << dp[n -1];
	return 0;
}