• 인프런의 김태원 강사님의 알고리즘을 공부하고 정리한 내용입니다.

냅백 문제는 언제 적용할 것인가?

: 구성요소가 많은데, 그 구성요소들을 이용해 어떤한 조건에 만족하는 값을 구할때 사용된다.
예를 들어서 2원과 3원을 이용해서 10원을 만드려고 할때의 최소 갯수는?

직감적으로 2원 2개와 3월 2개를 이용하면 10원을 만들수 있다.
이 때는 4개를 사용했다.
하지만 2원 5개로도 만들수 있다는 사실! 하지만 최소갯수 이므로 이때는 4개이다.
그런데 이거를 코드로 표현하기에는 좀 번잡하다.
어떻게 해야할지 막막하다.
왜냐하면
10을 가장 큰 3원으로 나누어서 진행할것인가를 생각할 수 있지만,
그렇다면? 3원으로 어디까지 나누어야 할것인가?
나머지가 나올때까지 ?? 그렇다면 이 조건은 말이 안된다.
나머지가 나온다면 3으로 3번 나누는데 나머지 1원은 어떻게 처리할것인가?

이와 같이 여러개를 조합해서 최소값이나 최대값을 도출하려고 할때 사용하자.

중요!

-> 여러 개의 요소들 중 타겟팅을 하나 골라서 일단 그 놈으로 먼저 진행하면서
다이나믹 테이블을 갱신하자.

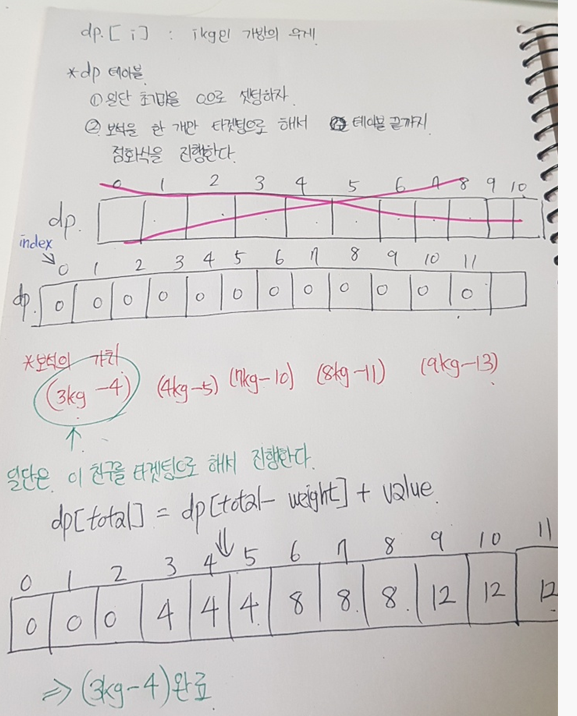
점화식

: ikg의 가방에 최대한 담을 수 있는 보석의 가치는?
dp[가방의 무게] = dp[가방의 무게 - 보석의 무게] + 보석의 가치
그리고 기존의 dp[가방의 무게] 와 비교를 한다.

진행과정

• 인덱스의 배수만큼만 dp에 셋팅하려고 했는데, 이렇게 하면 갱신이 안된다.
  테이블의 끝까지 민다는 개념으로 진행하자.

소스코드

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main()
{
	int n, limit;
	cin >> n >> limit;

	//무게 - 가치
	vector<pair<int, int>>gem(n);

	for (int i = 0; i < n; i++)
	{
		cin >> gem[i].first;
		cin >> gem[i].second;
	}

	vector<int>dp(limit +1);

	//4번 돌림
	for (int j = 0; j < n; j++)	
	{
		int weight = gem[j].first;
		//limit까지 돌림
		for (int i = weight; i <= limit; i++)
		{
			dp[i] = max(dp[i - weight] + gem[j].second, dp[i]);
		}
	}
	
	cout << dp[limit];
}

두번째 풀이 : 21년 10월 05일

#include <string>
#include <vector>
#include <algorithm>
#include <iostream>

using namespace std;



int main(void) {
	
	int n, m;
	cin >> n >> m;

	vector<pair<int, int>>v(n);
	vector<int>dp(m + 1, 0);

	for (int i = 0; i < n; i++)
	{
		cin >> v[i].first;
		cin >> v[i].second;
	}

	//보석의 갯수만큼 진행
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < m + 1; j++)
		{
			if (j - v[i].first >= 0)
			{
				int MAX = dp[j - v[i].first] + v[i].second;
				dp[j] = max(dp[j], MAX);
			}
				
		}
	}

	//for (int i = 0; i < dp.size(); i++)
	//	cout << dp[i] << endl;

	cout << dp[m];
}