부동 소수점과 고정 소수점.
- 38.456 의 실수가 있음.
고정소수점의 경우는 정수 : 38 , 소수부분 : 0.456 으로 나뉘어짐.
부동소수점의 경우는 유효숫자 : 38456 / 소수점 위치 : 3으로 구분됨.
-> 따라서 부동소수점을 이용하면 더 많은 범위를 표현할 수 있음.
메모리 구조에 대해서
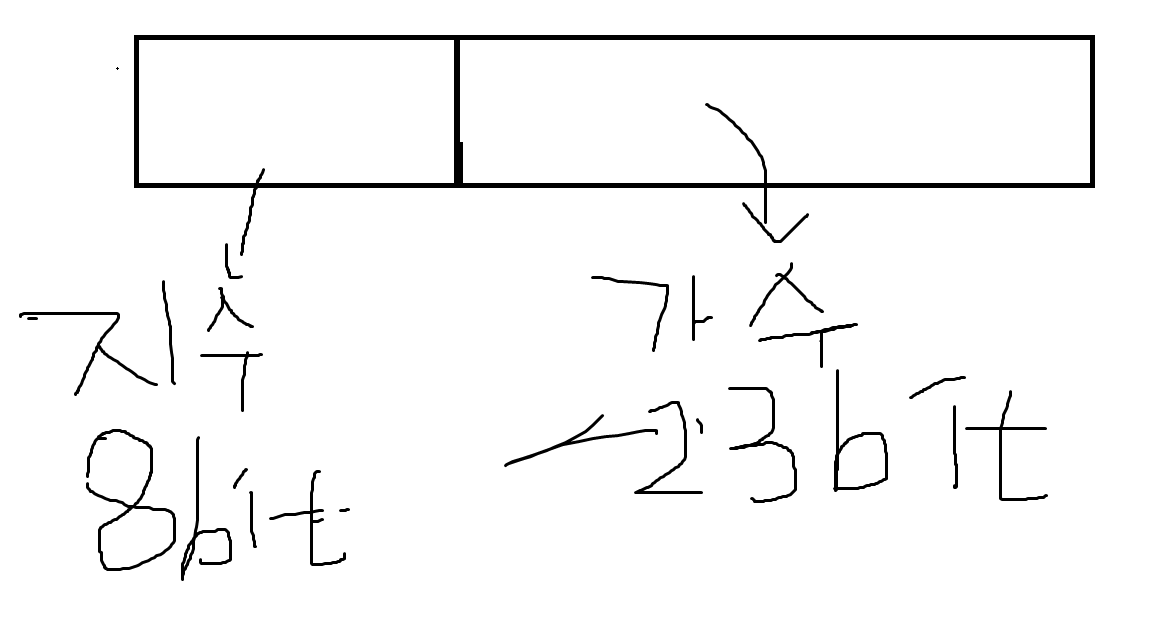
-
지수 부분은 8bit, 가수 부분은 23bit로 분류됨.
-
핵심!
but float이 2의 8승 미만만 나타낼수 있는 것을 아님.
엄청 큰 수를 표현하기 위해서는 가수부분의 23bit까지 가지고 와서 사용하는
구조임. -
만약 float으로 엄청 큰 숫자를 나타낸다고 했을 때, 소수점을 표현해야 하는
가수부분의 bit도 사용하므로, 소수점을 표현할 수 없음.
부동 소수점의 목적
- 1보다 작은 소수를 표현하는 것도 있지만, 아주 큰 수를 표현하는데에도 사용됨 .
예제
- 지수 부분의 크기 8을 벗어난 23bit의 수를 표현한다고 하면?
소수는 어떻게 표현될 것인가??
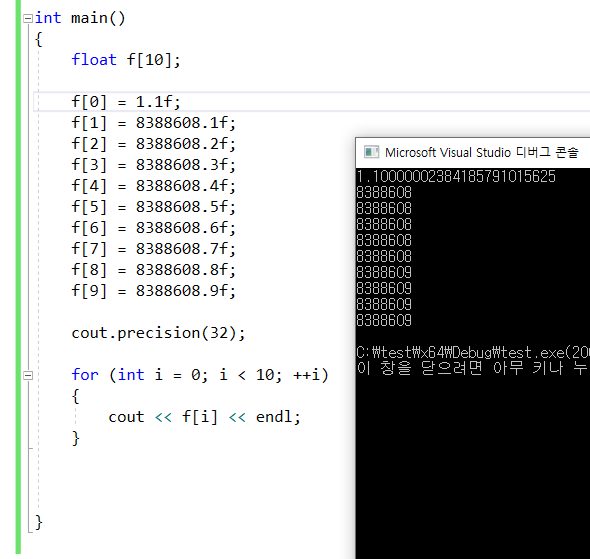
- 8388608 은 2의 23승임.
8388608 이상에서는 소수 부분을 표현할 수 없기 때문에, 소수 표현이 불가함 .
결론
- float형에서 지수 23이상인 숫자를 표현할 경우에는
소수점을 표현할 수 없음.
부동 소수점 정밀도 문제가 생기는 이유
: 부동소수점에 사용되는 23bit가 1보다 작은 소수 뿐 아니라,
엄청 큰 숫자에도 사용되기 때문임.
- 지수 부분에 들어가는 크기에 따라서 소수 표현 비트가 작아짐.
