첫번째 점화식
: 이중 포문으로, lis 방법으로 접근함.

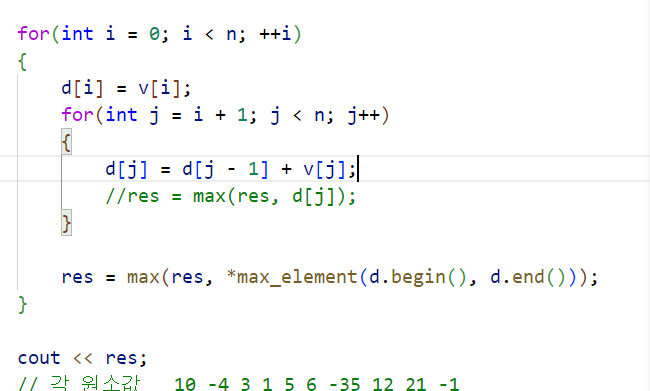
-> 시간 초과 발생함.
--> 다른 방법을 찾아보자.
두번째 접근방법.
:: 일단 입력값을 다시 한번 보면.

-> 여기서 결과 값이 나올수 있는 경우에 대해서 생각을 해보자.
10 -4 3 1 5 6 / 12 21임.
고찰
3 1 5 6 / 12 21 일까? 생각을 해찌만,
3 앞에 음수가 나왔지만, 전단계에서 엄청 큰수가 나오면, 차라리
3 기준으로 해서 2단계 앞까지 부터 진행하는 것이 훨씬 더
큰값을 가지게 됨.
--> 따러서 10 -4 3 1 5 6 으로 진행함.
// 음수일때를 조건으로 하는 것이 아님. 다른 방법이 있다라는 것을
생각해야 함.
=> -35 때문에 연속된 값이 끊김.
그 이후로 12 ,21 진행 하다고 -1값이 나오면서 끊김.
고찰
이전에 연속으로 진행한 값과 지금 v[] 값을 더하면서 비교를 통해
가장 큰값을 점화식에 추가해야 함을 느낄 수 있음.
d[n] : d[n - 1] + v[n] 이라고 할 수 있음.
추가적으로 d[n] 값과 비교를 해서 max로 지정하는 것이 나을듯 함.
그래야만, 10 -4 -> 이것도 갱신이 됨.
코드
#include <iostream>
using namespace std;
#include <vector>
#include <algorithm>
int main()
{
//freopen("input.txt", "r", stdin);
int n;
cin >> n;
vector<int> v(n);
vector<int> d(n);
for (int i = 0; i < n; ++i)
{
cin >> v[i];
}
int res = *max_element(v.begin(), v.end());
// lis 방식으로 접근하면 구할 수 있을 것 같음??
int start = 0;
int end = n - 1;
//10 -4 3 1 5 6 -35 12 21 -1
//d[n] : 인덱스 n부터 시작해서 마지막 인덱스까지 연속으로
// 더했을때 가장 큰값
// d[n] = arr[n]
// d[n] = arr[n] + d[n - 1]
d[0] = v[0];
for (int i = 1; i < n; ++i)
{
d[i] = v[i];
d[i] = max(d[i - 1] + v[i], d[i]);
}
cout << *max_element(d.begin(), d.end());
}