공식

• 점화식은 dp[a][b] : a에서 b로 가는데 k라는 경유점을 거치든 안거치든 최소 경로를 말한다.

1. 자기자신을 갈때는 비용을 0으로 한다.
2. a에서 b로 갈때 dist가 없다면 무한으로 설정한다.
3. 양방향으로 연결되어 있음에 유의하자.

풀이전략

• 모든 노드 간의 최소의 경로를 알아야 하므로 플로이드 워셜로 접근해야 한다.

• 플로이드 워셜 문제이다.

• 최대값 설정하는 것이 중요하다.
  : 문제에서 100000이 제한값이라고 해서 100001이라고 설정했는데,
  76점이 나왔다.

알아야 할점

• 최대값 설정
  문제에서 제한 사항이 n : 200개 이하.
  요금은 10만 이하라고 한다.
  경로가 없는 값은 무한이라고 생각하고, 코드를 짜지만, 무한이 없으므로 큰 값을 설정한다.
  : 문제에서 보면 연결되는 점이 없어서 경유해서 간다 치면, 모든 경로를 거치면 2000만의 값이 나오게 된다.
  마지막에 answer랑 2000만을 비교하는데, answer는 무제한 값을 의미하는 것이고, answer vs 2000만 비교해서 했을때 2000만 값이 나와야 하지만,
  answer가 2000만 보다 작으면 answer가 반환되는 문제가 발생한다.
  따라서 최대값 설정 고려를 해야 한다.

경유했을때 갈수없는 값도 2000만 보다 작다면
비교시 2000만이 나와야 하는데, 그보다 작은 값이 dp테이블에 저장될 것이므로
최대값을


두 군데 모두 고려해야 한다.

소스코드

#include <string>
#include <vector>

using namespace std;

int solution(int n, int s, int a, int b, vector<vector<int>> fares) {
    int answer = 0;

    vector<vector<int>>dp(n, vector<int>(n, 2000001));

    //놓친 부분
    for(int i = 0; i < n;i++)
    {
        for(int j = 0; j < n;j++)
        {
            if(i == j)
                dp[i][j] = 0;
        }
    }


    for(int i = 0; i < fares.size(); i++)
    {        
        dp[fares[i][0] - 1][fares[i][1] -1] = fares[i][2];   
        //놓친 부분
        dp[fares[i][1] - 1][fares[i][0] -1] = fares[i][2];         
    }

    //경유하는 점.
    for(int k = 0; k < n; k++)
    {
        //시작점
        for(int i = 0; i < n; i++)
        {
            //종점
            for(int j = 0; j < n; j++)
            {
                dp[i][j] = min(dp[i][k] + dp[k][j] , dp[i][j]);
            }
        }
    }

    s -= 1;
    a -= 1;
    b -= 1;

    answer = 2000001;
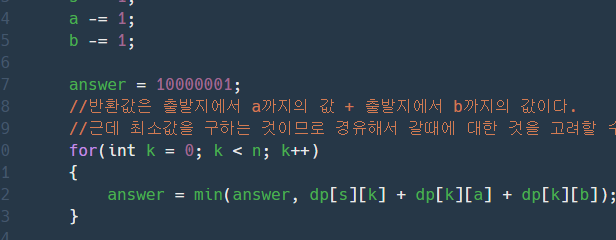
    //반환값은 출발지에서 a까지의 값 + 출발지에서 b까지의 값이다.
    //예시 2번을 보면 경유해서 간다.
    //근데 최소값을 구하는 것이므로 경유해서 갈때에 대한 것을 고려할 수 있다. 
    for(int k = 0; k < n; k++)
    {
        answer = min(answer, dp[s][k] + dp[k][a] + dp[k][b]);
    }


    return answer;
}

생각 많이 해야 할 부분

dp[s][a] + dp[s][b]를 하게 되면 7 + 7 + 11 이 나온다.
경유하는 구간이 dp[s][b] 이므로 이를 처리하기 위해서는
경유할때의 식을 다시 한 번 더 사용하면 된다.

//반환값은 출발지에서 a까지의 값 + 출발지에서 b까지의 값이다.
//예시 2번을 보면 경유해서 간다.
//근데 최소값을 구하는 것이므로 경유해서 갈때에 대한 것을 고려할 수 있다.
for(int k = 0; k < n; k++)
{
answer = min(answer, dp[s][k] + dp[k][a] + dp[k][b]);
}
요거를 어떻게 생각해 낼수 있냐면 3번 예제를 통해 고찰할 수 있다.
s -> b로 s - > a로 가는데 그대로 사용하면 7 + 7 + 11 -> 25이다.
시작점에서 경유점으로, 그리고 경유점에서 a와 b로 이동하는 것이
최저 비용으로 나타낼수 있따.