풀이전략

• 도달하는데 최소값을 구하는 문제이다.

• 경우의 수가 +2 인덱스 증가, + 1씩 인덱스 증가하는 부분이 있다.
  인덱스 간의 상호 관계를 나타내는 방법이므로
  dp로 접근해야 겠다고 판단

수도식은
dp[n] = min(dp[n -1] + 1, dp[n -2] +1);

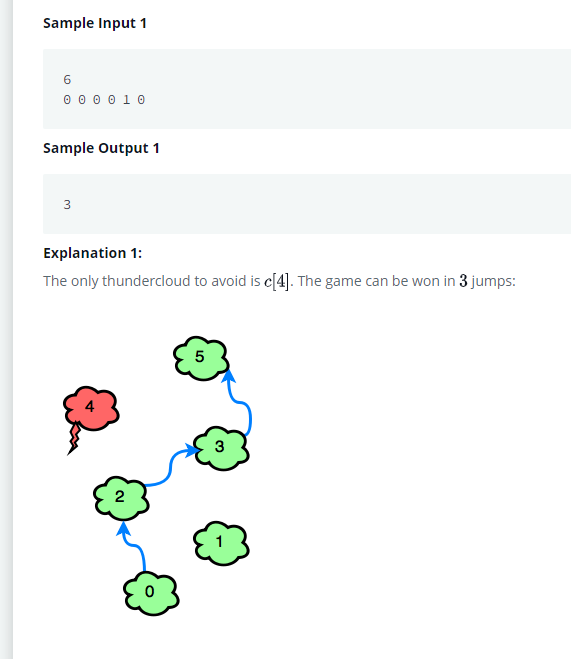
-> 이 그림을 보면
0 -> 2 -> 3 -> 5 도 가능하지만,
0-> 1 -> 3 -> 5도 가능하다.
dp를 통한 접근 방법이 맞다.

• 조건으로는 4번 구름은 2번과 3번 구름을 확인해야 하는데,,,
  4번은 현재 c[4]값이 0이므로, 위의 수도식은 불가능하게 하고,
  가장 큰값으로 설정하자.

최종 수도식
if(c[i] == 0)
{
dp[i] = INT_MAX;
}
else
{
dp[n] = min(dp[n -1] + 1, dp[n -2] +1);
}

dp[1]을 어떻게 처리할 것인가?? // 논리적인 문제

: dp[1]번을 어떻게 처리할지가 관건인데,, 어차피 dp[0]은 초기값이므로 0이다.
그렇다면 dp[2] 는 dp[1]과 dp[0]을 비교할 텐데 , dp[0]은 0이므로 dp[1]을 dp[0]과 연결된 값으로 보는 것이 적합하다.
dp[1]을 0으로 놓으면 어쨋든 최소값은 0이 나오지만, cp[1]이 1이더라도,
즉 빨간 구름일지라도, dp[0]이 0이므로 수도식에 영향을 끼치지는 않는다.
만약을 대비해서 dp[1]을 1로 설정하는 것이 타당하다.
-> 논리적으로 생각해야 한다.

소스코드

int jumpingOnClouds(vector<int> c) {

    int cnt = 0;
    const int size = c.size();
    vector<int>dp(size, INT_MAX);
    
    dp[0] = 0;
    dp[1] = 1; //어차피 0번 인덱스는 0이므로 1로 나두어도 무관하다
    for(int i = 2; i < c.size(); i++)
    {
        if(c[i] == 0)
            dp[i] = min(dp[i - 1] + 1 , dp[i -2] + 1); 
        else  
        {
            dp[i] = INT_MAX;
        }
    }
    
    cnt = dp[size -1];
    return cnt;
}