알고리즘 시간복잡도 BigO

해당 자료는 유튜브 신찬수 한국외대 교수님 강의를 시청하며 정리했습니다. 🙏🏻

앞서 4강에서 본 3개의 함수의 시간 복잡도:

• Algorithm1(arrayMax): T1(n) = 2n - 1
• Algorithm2(sum1): T2(n) = 4n + 1
• Algorithm3(sum2): T3(n) = (3/2)n2 - (3/2)n + 1

도출할 수 있는 명제:

• Algorithm2가 Algorithm1보다 2배 느리다.
• Algorithm3는 n < (5/3) 이면 Algorithm2보다 빠르다.
• Algorithm3는 모든 n에 대해서 Algorithm1보다 느리다.
• Algorithm3는 n > 5/3이면 항상 Algorithm2보다 느리다
  

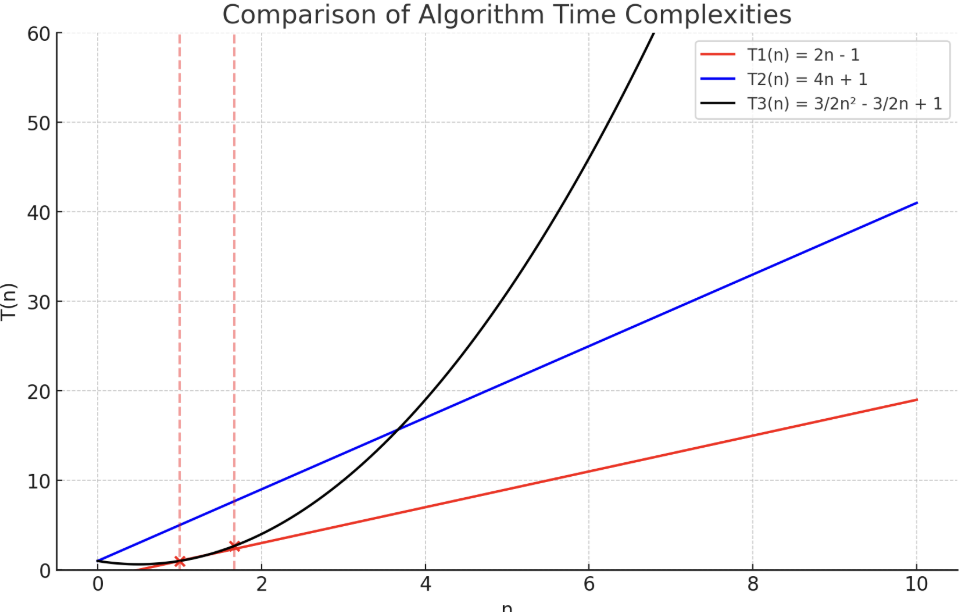
T1(n), T2(n)은 n에 대해 선형적으로 증가. 최고차항이 1차항
T3(n)은 n에 대해 제곱으로 증가. 최고차항이 n의 2제곱

n에 대한 최고차항 = 단위 시간의 증가율을 결정

Big-O 표기법

함수 값을 결정하는 최고차항만으로 간단하게 표기

T1(n) = 2n-1 => T1(n) = O(n)
T2(n) = 4n+1 => T2(n) = O(n)
T3(n) = 3/2n2-3/2n+1 => T3(n) = O(n^2)

표기방법

1. 최고차항만 남긴다.
2. 최고차항 계수(상수) 생략한다.
3. Big-O로 감싸서 적는다 => O(최고차항)

집합으로 이해하기

T1(n) = O(n)
T2(n) = O(n)
위 두 함수는 O(n) 집합 안에 들어있는 것으로 보면 된다.

즉,

T1(n) ∈ O(n)
T2(n) ∈ O(n)

문제 예시1

def increment_one(a):
	return a + 1

T1(n) = 1
=> 0(n^0)
=> O(1)

문제 예시2

def number_of_bits(n):
	count = 0
	while n > 0 :
    	n = n // 2
	    count += 1
        
	return count
	

n/2^count = 1
n = 2^count
10g2n = count
즉 while문 log2n번 실행

T(n) =C log2n + 1
=> O(log2n)