STFT

단시간 푸리에 변환

: 시간 도메인의 신호를 주파수 도메인으로 변환하는 방법
신호가 시간에 따라 어떻게 주파수적으로 변하는지를 분석할 수 있게 해줌
신호를 작은 시간 단위로 나누고, 각각의 단위에 대해 푸리에 변환을 수행함으로써 시간-주파수 분석을 가능하게 한다

STFT의 목적

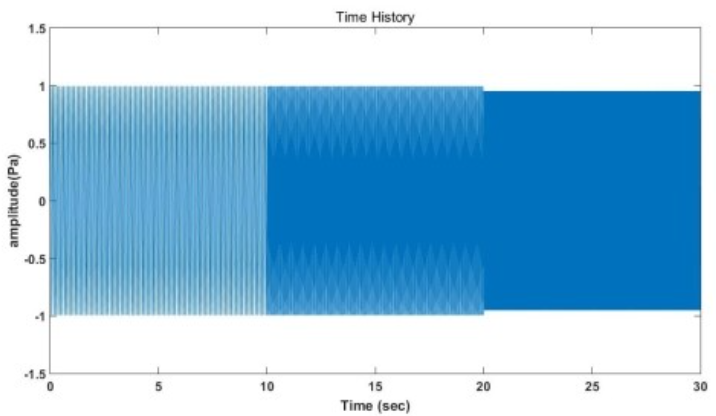
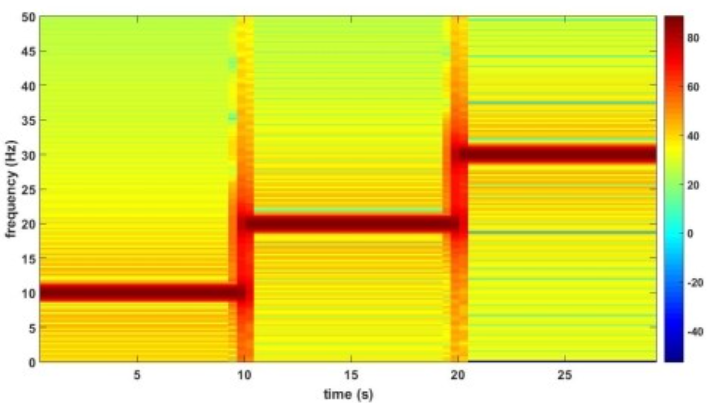
: 그래프가 시간과 주파수 2개의 축으로 이루어져 있음. 신호에 대해 자신이 알고 싶은 시점에서의 주파수 성분을 확인할 수 있다.

STFT 식

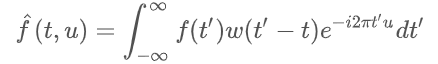
신호를 슬라이딩 윈도우 기법처럼 특정 길이를 가진 윈도우를 시그널 위에 움직이면서, 각각 윈도우에서 푸리에 변환을 하는 것
특정 시간 t에 대해 푸리에 변환을 여러 번 계산 -> 계산 횟수만큼 평균을 구해서 특정 시간 t에서의 주파수 스펙트럼을 구한다

• 변수 : 슬라이딩 윈도우의 크기

frequency와 time 사이 trade-off

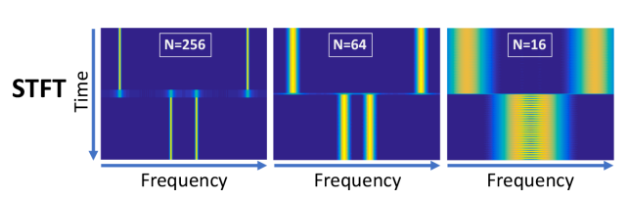
원도우의 크기가 작게 해서 개수를 늘이면 -> 결과가 대부분 유사 -> spread-out되어 -> 주파수 영역의 해상도가 떨어진다
원도우의 크기 크게 하면, 해상도는 올라가지만 시간 영역에 흐릿한 영역이 넓어짐
SOL)
높은 주파수는 윈도우 크기를 작게, 낮은 주파수는 윈도우 크기를 넓게 가져간다. but, 고정된 윈도우 사이즈에만 가능
SOL)

Wavelet Transform

cosine과 sine으로 구성된 기저함수로의 분해되는 푸리에 변환과 달리, 웨이블릿 변환은 ‘웨이블릿(wavelet)’이라는 기저함수로 분해된다.

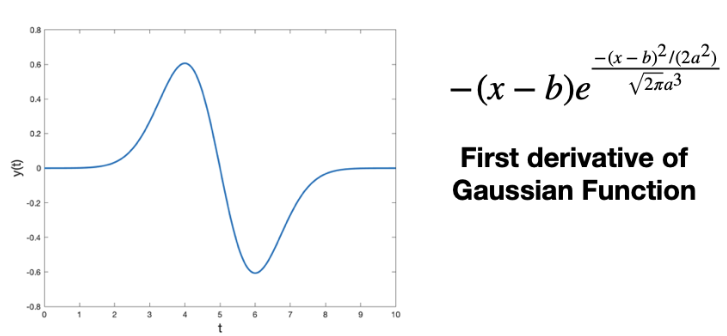
국소 시간 부분에만 파동이 존재하고, 대부분은 0의 값을 가지는 파동
웨이블릿 변환은 작은 주파수에 대해선 넓은 윈도우 크기를 가지고, 큰 주파수에 대해선 좁은 윈도우 크기를 가지기 때문에 시간과 주파수 두 영역 모두에서 높은 해상도를 가질 수 있게 되는 것

FT, STFT, WT 비교

웨이블릿 변환의 계산과정

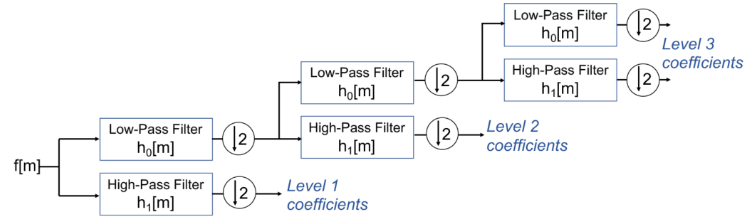
scale이 커질수록 주파수가 작아지기 때문에 국소 시간 부분의 크기가 증가 -> 여기에 맞춰서 scale이 커질수록 shift되는 정도도 큼직해야하고, 반면에 샘플링 정도는 작아져야 한다 -> 그렇게 되어야 시간-주파수 영역에서의 해상도를 유지할 수 있다

EEG와 STFT간의 관계

EEG 신호는 시간에 따른 전기 신호의 변화를 보여주는 시계열 데이터. 이 데이터를 STFT를 통해 주파수 도메인으로 변환하면, 각 시간 단위에서의 뇌파의 주파수 구성을 볼 수 있다. (즉, 뇌파가 어떤 주파수 성분을 가지는지, 그것이 시간에 따라 어떻게 변화하는지 파악 가능)
-> 특정 주파수의 뇌파가 강조되는 상황을 파악하거나, 뇌파의 주파수 패턴이 특정 상황과 어떻게 연관되는지를 분석하는 데 사용될 수 있다.