VQ-VAE

Abstract

감독 없이 유용한 표현을 학습하는 것 : 기계 학습의 주요과제
VAE와 다른 VQVAE 특징
1. 인코더 네트워크는 연속적인 코드 대신 이산적 코드 출력
이산 잠재 표현을 학습하기 위해 VQ와 아이디어 통합
-> VQ 사용하면, 모델이 강력한 자기회귀 디코더와 쌍을 이룰 때 잠재 변수가 무시되는 poesterior collapse 문제 우회 가능
2. 사전 분포가 정적이고 학습되지 않는다.

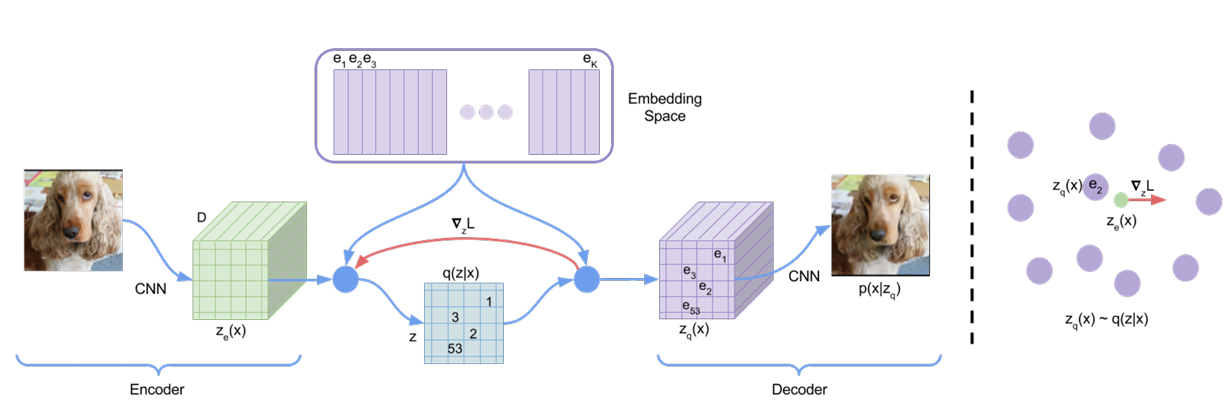
• 인코더 x의 출력은 가장 가까운 점 e에 매핑
• 기울기 ∇L은 인코더가 출력을 변경하도록 밀어낼 것이며, 이는 다음 순방향 전달에서 구성을 변경할 수 있음
  

왼쪽 : 원본 파형, 중간 : 동일한 화자 ID로 재구성 오른쪽 : 다른 화자 ID로 재구성
새 파형의 내용 동일

처음 6 프레니늠 모델에 제공되며, 다음 프레임은 작업에 따라 생성됨
상단:"앞으로 이동" 작업 반복
하단:"오른쪽 이동" 작업 반복

Introduction

최대 우도 최적화, 잠재 공간에서 데이터의 중요한 기능을 보존하는 모델 달성하는 것
"이산 표현"

• 간단하고 이산적인 잠재 변수를 사용하며 "후기 붕괴"에 시달리지 않고 분산 문제가 없는 VQ-VAE 모델을 소개한다
• 이산 잠재 모델(VQ-VAE)이 로그 우도에서 연속 모델과 동일한 성능을 발휘함을 보인다.
• 강력한 사전 분포와 결합될 때, 샘플은 음성 및 비디오 생성과 같은 다양한 응용 분야에서 일관되고 고품질이다.
• 어떤 감독도 없이 원시 음성을 통해 언어를 학습했다는 증거를 보여주고, 비지도 화자 변환의 응용 프로그램을 보인다

VQ-VAE

사후 및 사전분포는 범주형, 이러한 분포에서 추출된 샘플은 임베딩 테이블을 색인함
이러한 임베딩은 디코더 네트워크에 대한 입력으로 사용됨

3.1 Discrete Latent Variables

잠재 임베딩 공간 : $e \in R^{K \times D}$
K : 이산 잠재 공간의 크기
D : 각 잠재 임베딩 벡터의 차원

• 이산 잠재 변수 x는 공유 임베딩 공간e를 사용하여 가장 가까운 이웃 탐색을 통해 계산됨

• x가 주어졌을 때 이산 잠재 확률 변수 z의 사후 분포<사후 범주용 분포> q(z|x)
  
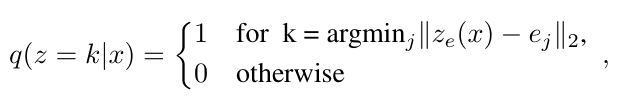
  e를 사용해 가장 가까운 이웃 탐색을 통해 계산됨
  $z_e(x)$ : 인코더 네트워크의 출력
  이 모델을 ELBO로 $\text{log } p(x)$를 경계로 할 수 있는 VAE로 본다.
  제안 분포 $q(z=k|x)$는 결정론적이며, z에 대한 간단한 균일 사전 분포를 정의함으로써 KL 발산 상수를 얻고 log K와 같게 된다
  $z_e(x)$ 표현은 이산화 병목을 통과한 후 식 1과 2에 주어진 임베딩 e의 가장 가까운 요소에 매핑됨

  디코더의 입력 : $e_k$
  

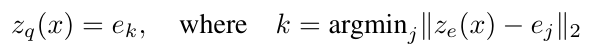
• 이 순방향 계산 파이프라인은 잠재 변수를 1ofK 임베딩 벡터에 매핑하는 특정 비선형성을 가진 일반적인 오토인코더로 볼 수 있다.
  모델의 전체 매개변수 집합은 인코더, 디코더, 임베딩 공간 e의 매개변수의 합집합

  3.2 Learning

  gradient 계산이 어려운 이유는 VQ-VAE에서 사용하는 quantization이 비연속적인 연산이라서 진짜 gradient 계산 불가
  -> decoder 쪽에서 계산된 gradient를 encoder에 복사해서 쓰는 방식 STE(straight-through estimator)을 쓴다

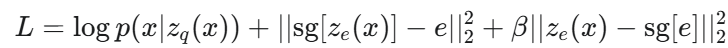
1. reconstruction loss
   decoder가 quantized latent $𝑧_𝑞(𝑥)$로부터 입력 x를 얼마나 잘 복원하는지를 측정하는 항

• 최대한 크게
• decoder와 encoder가 같이 영향을 받음

2. codebook loss

• codebook e가 encoder출력 $z_e(x)$에 더 가까워지도록 유도
• sg는 stop-gradient:
  $𝑧_𝑒(x)$는 고정하고 𝑒만 학습하겠다는 의미

기존 : gd로 e update
가까운 $z_e(x)$의 평균으로 e 업데이트

• minibatch는 불가능
  해결 : EMA
  

3. commitment loss

• encoder가 codebook에 가까이 붙도록
• sg[e]는 codebook 벡터를 고정하고 $𝑧_𝑒(x)$만 학습한다는 뜻.

• sg[] : $z_e(x)$를 그대로 쓰지만, gradient는 전달하지 않음

3.3 Prior

사전분포 p(z) : 잠재변수 z가 어떤 값을 가질 확률인지를 입력 x를 보기 전에 정의한 확률 분포(데이터가 없을 때 잠재 공간에서 어떤 값이 더 가능성이 높은지를 나타내는 믿음)

p(z)가 필요한 이유 : VQ-VAE는 오토인코더 구조이지만 생성모델이라서
z를 사전분포 p(z)에서 샘플링 -> 디코더에 넣어서 가까 이미지 생성