정규화(1차 2차 3차 BCNF)란?
- 데이터베이스의 설계를 재구성하는 테크닉입니다.
- 다시말해,
데이터 무결성을 유지하기 위해중복성을 최소화하고정보의 일관성을 보장하기 위한 개념입니다. - 이를통해 삽입/갱신/삭제 시 발생할 수 있는 각종
이상현상(Anamolies)들을 방지할 수 있습니다.
[이상현상(Anamolies) 정의 & 종류]
이상현상(Anamolies) 정의
: 잘못된 릴레이션 설계로 예기치 못한 현상이 발생하는 것
이상현상(Anamolies) 종류
- 삽입 이상 (Insertion Anomaly)
기본키가 {Student ID, Course ID} 인 경우 -> Course를 수강하지 않은 학생은 Course ID가 없는 현상이 발생함. 결국 Course ID를 Null로 할 수밖에 없는데, 기본키는 Null이 될 수 없으므로, Table에 추가될 수 없음.굳이 삽입하기 위해서는 '미수강'과 같은 Course ID를 만들어야 함.
불필요한 데이터를 추가해야지, 삽입할 수 있는 상황 = Insertion Anomaly
- 갱신 이상 (Update Anomaly)
만약 어떤 학생의 전공 (Department) 이 "컴퓨터에서 음악"으로 바뀌는 경우.모든 Department를 "음악"으로 바꾸어야 함. 그러나 일부를 깜빡하고 바꾸지 못하는 경우, 제대로 파악 못함.
중복된 데이터중 일부만 수정되어 데이터 모순이 일어나는 현상 = Update Anomaly
3. 삭제 이상 (Deletion Anomaly)
만약 어떤 학생이 수강을 철회하는 경우, {Student ID, Course ID, Department, Course ID, Grade}의 정보 중Student ID, Department 와 같은 학생에 대한 정보도 함께 삭제됨.
어떤 정보를 삭제할때, 의도하지 않은 정보까지 삭제가 되어버리는 현상 = Deletion Anomaly
정규화
1NF(제 1정규형)
: 도메인이 원자값만 가지도록 분해
각 로우마다 컬럼의 값이 1개씩만 있어야 합니다. 이를 컬럼이 원자값(Atomic Value)를 갖는다고 합니다.
- 제 1정규형 만족 X
위와 같은 경우에 John의 과목이 Math와 Music 두 개 이기 때문에 제 1정규형을 만족하지 못합니다.
- 제 1정규형 만족 O
2NF(제 2정규형)
: 제 1정규형 만족하고, 부분 함수 종속 제거
부분 함수 종속 제거
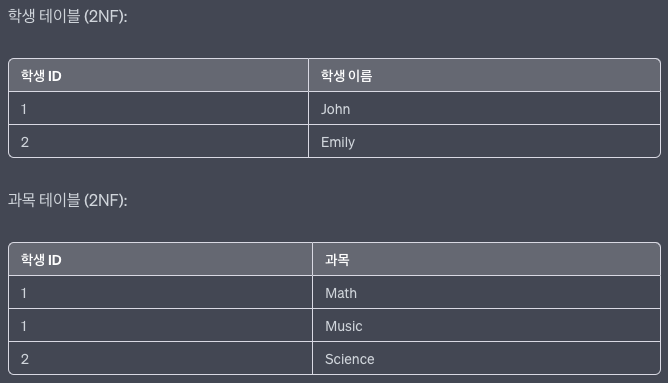
- 제 2정규형 만족 X
위 테이블의 경우 기본키는 (학생ID, 과목) 두 개로 볼 수 있습니다. 이 두 개가 합쳐져야 한 로우를 구분할 수가 있습니다. 근데학생이름의 경우 이 기본키중에학생ID에만 종속되어 있습니다. 즉,학생ID컬럼의 값을 알면학생이름의 값을 알 수 있습니다. 따라서학생이름이 두 번 들어가는 것은 불필요한 것으로 볼 수 있습니다.
- 제 2정규형 만족 O
3NF(제 3정규형)
: 제 2정규형 만족하고, 이행적함수 종속 제거
이행적함수 종속이란?
: 릴레이션에서 X, Y, Z라는 3 개의 속성이 있을 때 X→Y, Y→Z 이란 종속 관계가 있을 경우, X→Z가 성립될 때 이행적 함수 종속이라고 합니다.
이행적함수 종속 제거
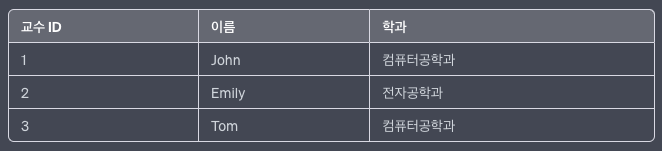
- 제 3정규형 만족 X![]
위 테이블에서학과는교수 ID에만 종속되어야 합니다. 하지만학과는교수 ID이외의 후보키인이름에도 종속되어 있습니다.
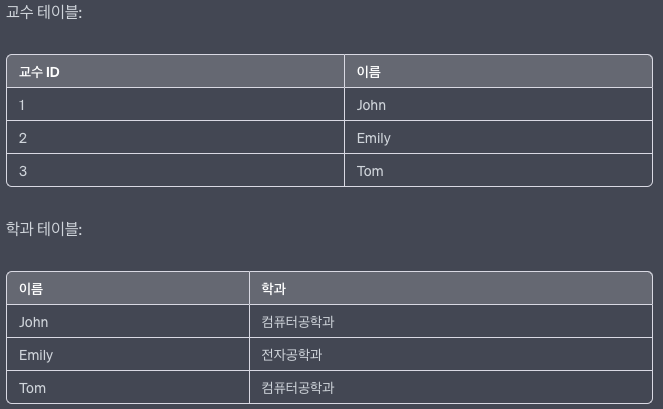
- 제 3정규형 만족 O
BCNF(보이스 코드 정규형)
: 제 3정규형을 만족하고, 결정자가 후보키가 아닌 종속 제거
결정자: 어떤 속성의 값을 결정하는 속성들을 말한다.
후보키: 기본키로 사용할 수 있는 속성들을 말한다.
모든 결정자가 후보키 집합에 속해야 한다.
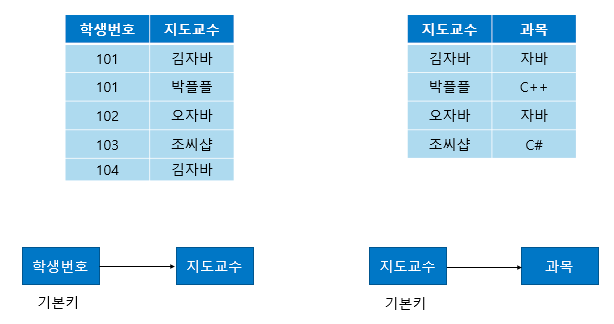
- BCNF(보이스 코드 정규형) 만족 X
위의 테이블은 (학생번호, 과목)이 기본키로 지도교수를 알 수 있다. 그러나 지도교수를 알면 과목을 알 수 있으므로, 지도교수 → 과목 이 종속적이다.
즉, 후보키 집합에 속하지 않은 결정자가 존재하므로 BCNF를 만족하지 않는다.- BCNF(보이스 코드 정규형) 만족 O!
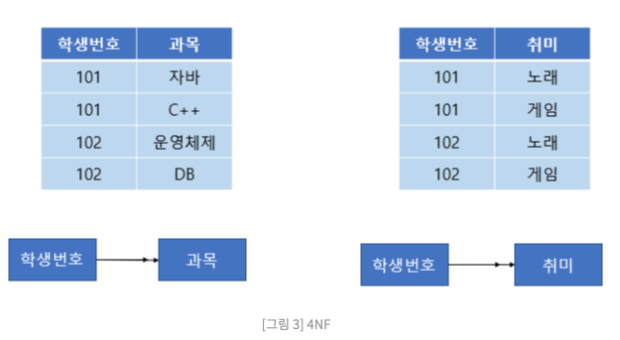
4NF(제 4정규형)
: BCNF(보이스 코드 정규형)을 만족하고, 다치 종속 제거
💡
다치 종속 (Multi-valued Dependency): 같은 테이블 내의 독립적인 두 개 이상의 컬럼이 또 다른 컬럼에 종속되는 것을 말한다.
다치종속성의 조건
① A->B 일 때 하나의 A값에 여러 개의 B값이 존재하면 다치 종속성을 가진다고 하고 A↠B라고 표시한다.
② 최소 3개의 컬럼이 존재한다.
③ R(A, B, C)가 있을 때 A와 B 사이에 다치 종속성이 있을 때 B와 C가 독립적이다.
- 제 4정규형 만족 X
- 제 4정규형 만족 O
5NF(제 5정규형)
: 제 4정규형을 만족하고, 조인 종속을 제거한다
- 4정규형에서 조인해보고 4정규형 전과 다르면(추가적으로 생겼으므로) 5정규형 만족하지 않는다. (즉, 조인을 통해 확인해봄)
💡
조인 종속 (Joint dependency)
하나의 릴레이션을 여러개의 릴레이션으로 분해하였다가, 다시 조인했을 때 데이터 손실이 없고 필요없는 데이터가 생기는 것을 말한다. 조인 종속성은 다치 종속의 개념을 더 일반화한 것이다.
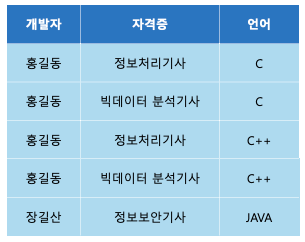
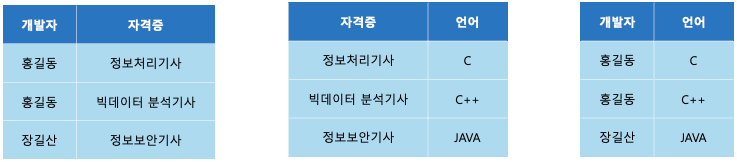
위의 4NF 테이블에 대해 조인 연산을 수행하면 다음과 같은 결과가 나온다.
- 제 5정규형 만족 X
위의 결과를 보면 제 4정규화를 수행하기 전 데이터와 다른 것을 알 수 있다.
데이터 손실은 없지만 필요없는 데이터가 추가적으로 생겼으므로 5NF를 만족하지 않는다.- 제 5정규형 만족 O
Q) 정규화를 하는게 무조건 좋은가 ?
답변 : 무조건 좋은 것은 아니다!!
데이터베이스 테이블을 생성하는데 필요한 용량은 크게 다음 두 가지 요소에 의해 결정됩니다.
[공간적인 측면]
- [장점] 중복 제거로 인해 테이블내 데이터 감소
: 정규화를 수행하면 테이블이 분리되어 데이터가 중복되지 않게 됩니다. 이로 인해 저장 공간의 효율성이 향상될 수 있습니다. 중복 데이터를 제거하고 테이블을 분리함으로써 불필요한 데이터 복제를 방지할 수 있습니다.
- [단점]: 데이터 분리로 테이블 생성
: 테이블 분리로 인해 추가적인 테이블이 생성되므로, 일부 상황에서는 저장 공간의 사용량이 증가할 수 있습니다.
🗣️ [테이블 데이터 vs 테이블 메타 데이터] 어떤게 더 많은 공간 차지 하는가?
- 테이블 메타데이터: 테이블의 스키마(열의 이름, 데이터 유형 등), 인덱스, 제약 조건 등에 관한 정보를 저장하기 위한 공간입니다. 이 부분은 일반적으로 작은 공간을 차지합니다.
- 테이블 데이터: 테이블의 행에 대한 실제 데이터를 저장하기 위한 공간입니다.
즉, 일반적으로 테이블 메타 데이터(테이블을 늘리는 것)가 더 작은 공간을 차지함
[시간적인 측면]
- [장점] 중복성이 줄어 시간 감소
:정규화된 데이터는 일반적으로 조회 작업에서 성능이 향상됩니다. 데이터의 중복성이 줄어들어 복잡한 연산 없이도 데이터를 효율적으로 조회할 수 있습니다.
- [단점] 조인 연산으로 인한 시간 증가
: 테이블 분리로 인해 조인 연산이 필요할 수 있으며, 이는 일부 작업에서 성능 저하를 초래할 수 있습니다. 테이블 간의 관계를 맺는 조인 연산은 추가적인 처리 비용이 발생할 수 있기 때문입니다.
결론
따라서, 정규화는 데이터의 일관성과 효율성을 향상시키는데 도움을 주지만, 상황에 따라서는 공간과 시간 측면에서 비용이 발생할 수 있습니다. 그러므로, 상황에 맞게 적절한 정규화 수준을 선택하는 것이 중요합니다.