[PS] BOJ 12865 : 평범한 배낭

Greedy vs. DP

작년 알고리즘 수업에서 Greedy Algorithm과 Dynamic Programming의 공통점과 차이점에 대해서 공부했었다.

너무나도 유명하고 굉장히 자주 쓰이는 이 두 알고리즘 계획법은 언뜻 보면 별로 다르지 않은 것 같아도 차이점이 분명히 있다.

두 알고리즘 계획법이 비슷해보이는 이유는 두 계획법 모두 다 optimal substructure를 사용하기 때문이다. 여기서 optimal substructure라는 것은, 어떠한 문제에 대한 optimal solution이 그 문제의 subproblem에 대한 optimal solution을 포함하고 있다는 것이다. 하지만 DP에서는 (일반적으로) bottom-up 방식으로 작은 subproblem에서부터 solution 탐색을 진행하고, 그리디는 solution을 찾는 과정에서 그 순간 가장 효율적인 선택을 진행한다는 점에서 차이가 있다.

그렇기 때문에 DP로 풀리는 문제가 그리디로 풀리지 않을 수도 있고, 그리디로 풀리는 문제가 DP로 풀리지 않을 수도 있다.

이것의 가장 대표적인 예시가 바로 Knapsack Problem, 일명 배낭 문제이다.

Knapsack Problem

Knapsack Problem은 최대 $W$의 무게만큼의 물건을 담을 수 있는 배낭이 있고, 배낭에 담을 $n$개의 물건이 있는 상황에서 $i$번째 물건의 무게가 $w_i$, 가치가 $v_i$일때 배낭에 담을 수 있는 물건들의 총 가치를 최대로 하는 방법 또는 그 최대의 가치 값을 찾는 문제이다.

여기서 세부적인 문제 상황에 따라 또 Knapsack Problem은 두 가지로 나뉜다.

1) fractional knapsack problem
fractional knapsack의 경우 각각의 물건을 부분적으로 취해서 배낭에 담을 수 있다.
이 경우에는 문제가 매우 쉬워진다. 바로 Greedy Algorithm을 사용하면 된다!

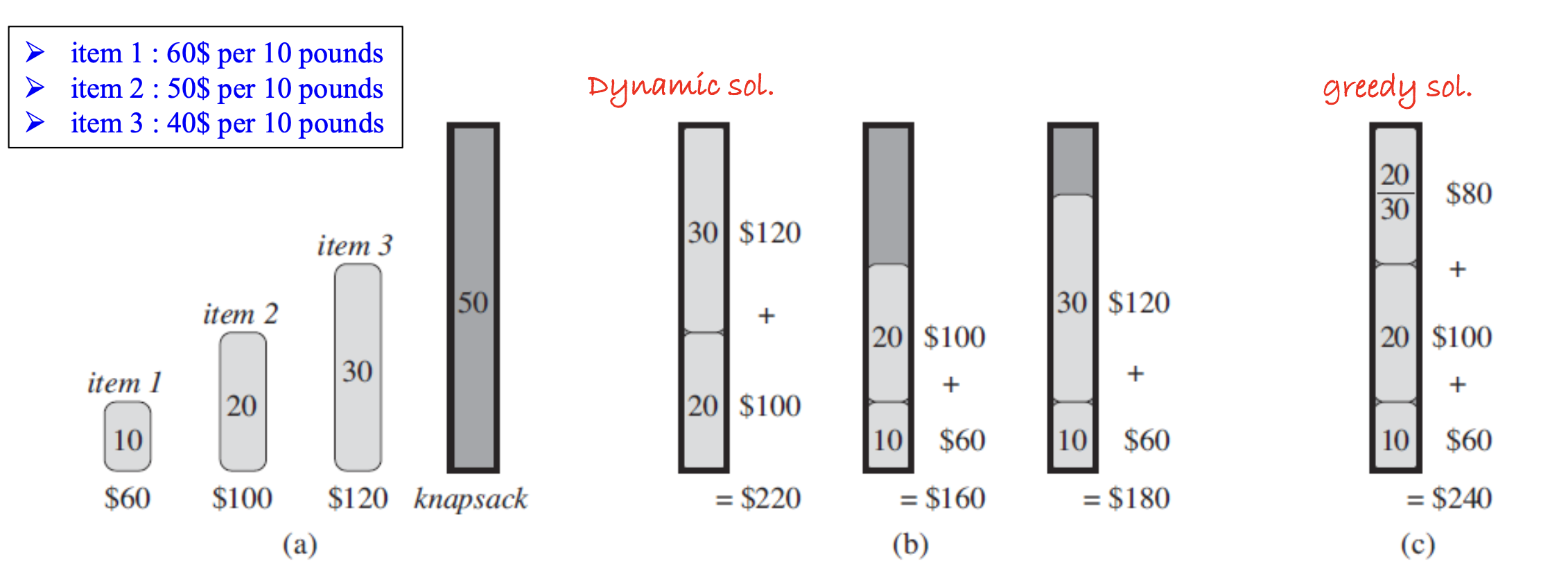
위 그림에서 볼 수 있듯이, 각각의 물건들에 대해서 단위 무게 당 가치를 계산한 다음 그 가치가 가장 높은 물건부터 전부 배낭 안에 담고, 다음으로 높은 물건을 또 배낭 안에 담고를 반복하면서 배낭을 꽉 채우면 된다. 해당 물건을 전부 담을 자리가 없다고 해도 부분적으로 취해서 담으면 되기 때문에 greedy한 방식으로 문제를 해결할 수가 있다.

2) 0-1 knapsack problem
하지만, 어떤 물건을 부분적으로 취할 수가 없고 반드시 담을 지 혹은 담지 않을지 둘 중에 하나만 선택할 수 있는 0-1 knapsack의 경우 greedy solution이 optimal solution임을 보장할 수 없다. 실제로 위 예시에서도 볼 수 있듯이 greedy한 solution은 $160의 가치를 갖지만 최적해는 $220의 가치를 가지고 있다.

그렇다면 이런 0-1 knapsack problem의 경우 어떻게 최적해를 찾을 수 있을까?

대표적인 풀이 방법에는 2차원 DP가 있다.

How to find a solution of 0-1 Knapsack

예제와 함께 원리를 이해해보자.
예제는 실제 백준 예제 입/출력에 있는 테스트 케이스로 진행해보자.
첫 줄의 값은 순서대로 item의 개수 $N=4$, 배낭에 담을 수 있는 최대 무게 $K=7$이다.

4 7 
6 13
4 8
3 6
5 12

1) 먼저, 모든 item들을 weight가 작은 순서대로 정렬하고, 각각의 item을 $i_1$, $i_2$, ... , $i_N$라고 하자. 각각의 item은 weight와 value 값 $(w_{i_n}, v_{i_n})$을 갖는다.

예제에서는
$i_1 : (3, 6), i_2 : (4, 8), i_3:(5,12),i_4:(6,13)$이 될 것이다.

2) 다음과 같은 2차원 테이블을 만들어보자.

그리고 해당 테이블에서 $i_n$번째 열, $w$번째 행의 값을 $V(i_n, w)$라고 하고 $V$에 대한 점화식을 다음과 같이 정의한다.

$V(i_n, w) = \begin{cases} 0 & n=0\ or\ w=0\\ \begin{cases} max(V(i_{n-1},w), v_{i_n}+V(i_{n-1}, w-w_{i_n})) &if\ w-w_{i_n} \ge 0 \\ V(i_{n-1},w) & otherwise\\ \end{cases} & otherwise \end{cases}$

위 수식을 이해해보자.
우리는 $V(i_n,w)$라는 값을 최대 담을 수 있는 무게를 $w$라고 하고 $n$번째 item까지 체크했을 때 얻을 수 있는 최대 value 값 이라고 생각할 것이다. 이 말은 결국 $V(i_N, w)$은 모든 item을 고려한 값이기 때문에 최대 담을 수 있는 무게를 w라고 했을 때의 optimal solution이라는 것이다.

먼저, $n$이 0인 경우는 당연히 값이 0이 될 것이다.

$w$는 해당 행에서 우리가 최대로 담을 수 있는 무게다. 그렇다는 말은 $i_n$의 weight가 $w$를 넘지 않는 경우에만 우리는 해당 item을 배낭에 담을 수 있는 것이다. 해당 item을 담지 못한다면, 그냥 $i_{n-1}$까지 체크한 값과 동일할 것이다.

만약 해당 item을 담게 된다면, 해당 item의 value 값과 $V(i_{n-1}, w-w_{i_n})$을 더해줘야 한다. 그 이유는 해당 item을 담고 나서 이제 담을 수 있는 물건들의 최대 무게는 $w-w_{i_n}$이 될 것이고, 해당 행에서 $i_n$을 체크하기 직전 가장 마지막으로 체크한 item은 $i_{n-1}$이 될 것이기 때문에 해당 item까지 체크해준 값을 반영해주면 되는 것이다.

또한, 이 모든 계산은 현재 item들이 weight가 낮은 친구부터 순서대로 정렬되어 있기 때문에 가능하다. 기본적으로 이 풀이 또한 optimal substructure를 기반으로 한다. weight가 낮은 item부터 우선적으로 고려하기 때문에 우리는 각각의 $V(i_n, w)$ 값을 해당 상황에서의 최댓값이라고 이야기할 수가 있는 것이다. (실제 구현도 이렇게 점화식을 세운다면 반복문을 돌면서 index 0부터 체크해주면 되니까 훨씬 편할 것이다.)

예를 들어, 우리가 원하는 답을 최초로 얻게 되는 $V(i_2, 7)$을 보면 이 값은 $i_2$을 배낭에 담았기에 얻을 수 있는 value인 $v_{i_2}=8$과 남아있는 무게 $w-w_{i_2}=7-4=3$을 최대 무게라고 했을 때, $i_2$를 제외하고 이전의 item $i_1$까지 고려했을 때의 최대값인 $V(i_1, 3) = 6$을 더해준 값이 되는 것이다.

이 방식을 토대로 첫 번째 행부터 $K$번째 행까지 차례대로 값을 계산해주면 되고, 최종적으로 우리가 구하고자 하는 optimal solution 값은 $V(i_N, k)$가 될 것이다~

Code

위를 구현한 실제 코드는 다음과 같다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

bool cmp(pair<int, int> a, pair<int, int> b){
    if(a.first == b.first) return a.second < b.second;
    else return a.first < b.first; //weight 순서로 정렬
}

int main(){

    int N, K;
    cin >> N >> K;

    vector<pair<int, int> > item_list; //(w, v)
    
    int w, v;
    for(int i=0;i<N;i++){
        cin >> w >> v;
        item_list.push_back(make_pair(w, v));
    }
    sort(item_list.begin(), item_list.end(), cmp);

    int min_weight = item_list[0].first;

    int ** V = new int *[K+1];
    for(int i=0;i<=K;i++){
        V[i] = new int[N+1];
    }

    for(int i=0;i<=K;i++){
        for(int j=0;j<=N;j++){

            if(i < min_weight || j == 0) V[i][j] = 0;
            else{
                int w_j = item_list[j-1].first;
                int v_j = item_list[j-1].second;

                if(i - w_j >= 0) 
                    V[i][j] = max(V[i][j-1], v_j + V[i - w_j][j-1]);
                else
                    V[i][j] = V[i][j-1];
            }
        }
    }

    cout << V[K][N] << endl;

    for(int i=0;i<=w;i++){
        delete[] V[i];
    }
    delete[] V;

    return 0;

}

특별할 거 없이, 그냥 위에 설명해놓은 알고리즘을 코드로 구현한 것이다.

마치며

2차원 DP를 실제로 이해하고 구현하려고 하니 꽤 골치가 아팠다.
1차원으로 된 DP는 점화식 세우기 쉬워서 금방금방 풀었었는데 확실히 그거보다는 훨씬 어려웠다. 연습을 좀 많이 해 볼 필요성이 있는 것 같다.
knapsack knapsack 맨날 말만 들었었는데 풀어보니 신기했다.
greedy랑 dp는 PS하면 계속 나올 알고리즘 기법들이니 확실히 이해해둬야겠다.