안녕하세요!
오늘도 어김없이 자료구조 시간입니다^^,,,
생각보다 매일매일 포스팅해서 올리는게 고된 과정이네요 (파워개발블로거분들 존경)
오늘 주제는 Heap 자료구조입니다!
스택, 큐, 덱을 꼼꼼하게 정리하셨다면 Heap도 쉽게 이해할 수 있을 거라고 생각합니당
그럼 시작해볼까요?
1. 개념
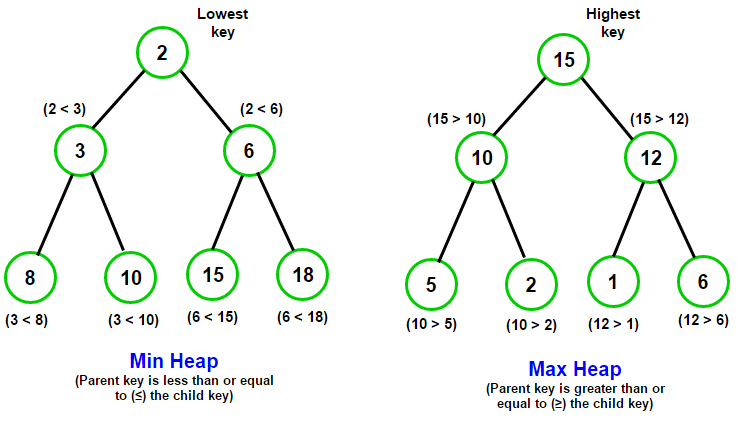
Heap - 힙은 *우선순위 큐를 위해 고안된 완전이진트리 형태의 비선형 자료구조입니다.
힙에 저장된 노드를 꺼내면 우선순위(값)가 높은 데이터 순으로 나오게 됩니다.
따라서 힙은 여러 데이터 값들 중, 최대 값과 최소 값을 빠르게 찾을 수 있도록 해줍니다.
Q. 우선순위 큐란?
A. 들어온 데이터 순서대로 반환되는 것이 아닌, 부여된 우선순위를 기준으로 데이터 반환이 이루어지는 큐를 의미합니다.
힙의 주요 특징은 아래와 같습니다.
-
완전이진트리 형태를 가지고 있습니다.
-
자식 노드는 부모 노드 값만 고려하면 되는 ‘반정렬 상태’을 유지합니다.
-
중복 값이 허용됩니다.
-
최대 힙과 최소 힙이 있습니다.
힙의 종류가 두가지이니 각각의 구조와 저장방식에 대해 알아보겠습니다.
1-0. 왜 Heap이 만들어졌나?
힙에 대해 정리하는 과정에서 생긴 궁금증입니다.
어딜 가든 모두 힙은 ‘우선순위 큐를 위해 만들어진/사용되는 자료구조다’ 라고 말하고 있었습니다.
그렇다면 배열이나, 연결리스트로는 우선순위 큐를 구현할 수 없는 걸까요?
(1) 배열로 구현했을 경우
배열로 우선순위 큐를 만든다고 가정해보겠습니다.
만약 우선순위가 높은 데이터를 배열의 앞부분부터 삽입한다면, 가장 앞의 인덱스를 이용하여 반환하면 되므로 구현이 어렵지 않습니다.
하지만 세상은 그렇게 친절하지 않습니다.
만약 중간에 우선순위가 갱신되는 경우 뒤에 있는 모든 데이터를 한 칸 씩 뒤로 옮겨야합니다. 또한 들어가야할 위치도 탐색해야하죠.
즉, 배열로 구현하는 경우 삭제는 O(1), 삽입은 O(n) 이 걸리게 됩니다.
(2) 연결리스트로 구현한 경우
이번엔 연결 리스트로 우선순위 큐를 만든다고 가정해보겠습니다.
연결리스트는 배열과 달리 뒤의 데이터를 한 칸 씩 밀지 않아도 됩니다.
문제는 데이터가 들어갈 자리를 탐색해야합니다. 최악의 경우 모든 데이터를 거쳐가야 할지도 모릅니다.
즉, 연결리스트로 구현하는 경우 역시 삭제는 O(1), 삽입은 O(n) 이 걸리게 됩니다.
이처럼 다른 자료구조로도 ‘구현’은 할 수 있습니다. 성능이 좋지 않을뿐,,
그럼 힙으로 구현하는 경우는 다를까요? 완독하면 궁금증이 풀리실 겁니다ㅎㅎ
1-1. Max Heap
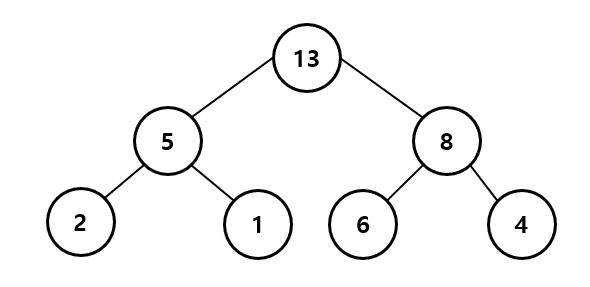
최대 힙은 자식 노드에서 루트 노드로 올라갈 수록 저장된 값이 커지는 구조입니다
루트 노드가 가장 큰 값을 가지고 있고, 자식 노드는 부모 노드보다 작거나 같은 값을 가지고 있습니다.
(1) 삽입
-
최대 힙에 새로운 데이터가 들어오면 일단 리프 노드 마지막에 이어서 삽입합니다.
-
이후 부모 노드의 값과 비교하면서 최대 힙의 구조를 만족하도록 자리를 변경합니다.
예시를 통해 확인해 보겠습니다!
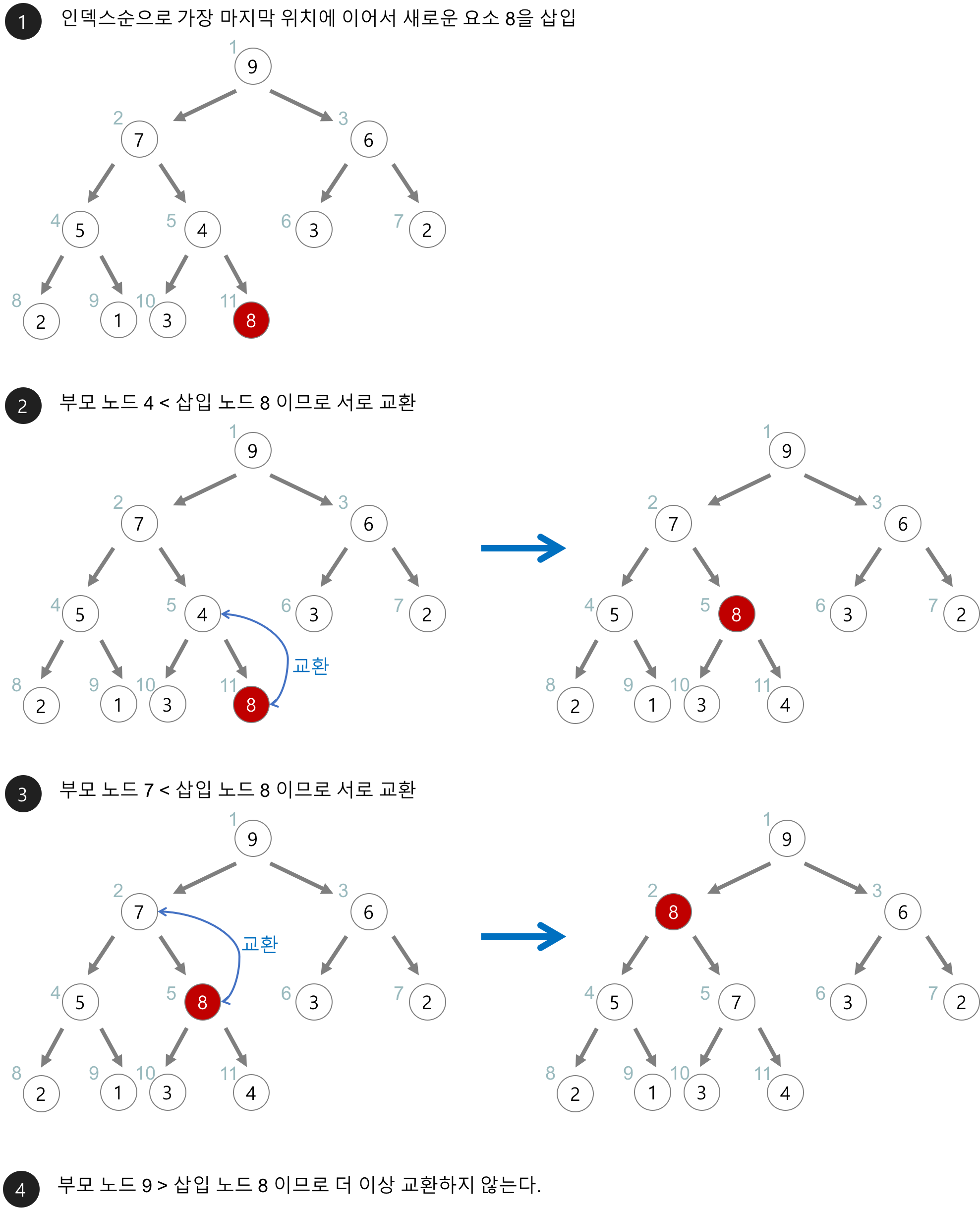
위처럼 새로운 값 8 을 삽입하는 경우, 기존의 7보다 큰 값이기 때문에 부모노드와 비교하면 순차적으로 올라오게 됩니다.
(2) 삭제
-
최대 힙에서 데이터를 꺼내는 경우 가장 큰 데이터를 꺼내는 것이므로 루트 노드가 삭제됩니다.
-
삭제된 루트 노드 자리에 리프 노드의 가장 마지막 데이터를 가져옵니다.
-
이후 자식 노드의 값과 비교하면서 최대 힙의 구조를 만족하도록 자리를 변경합니다.
예시를 볼까요?
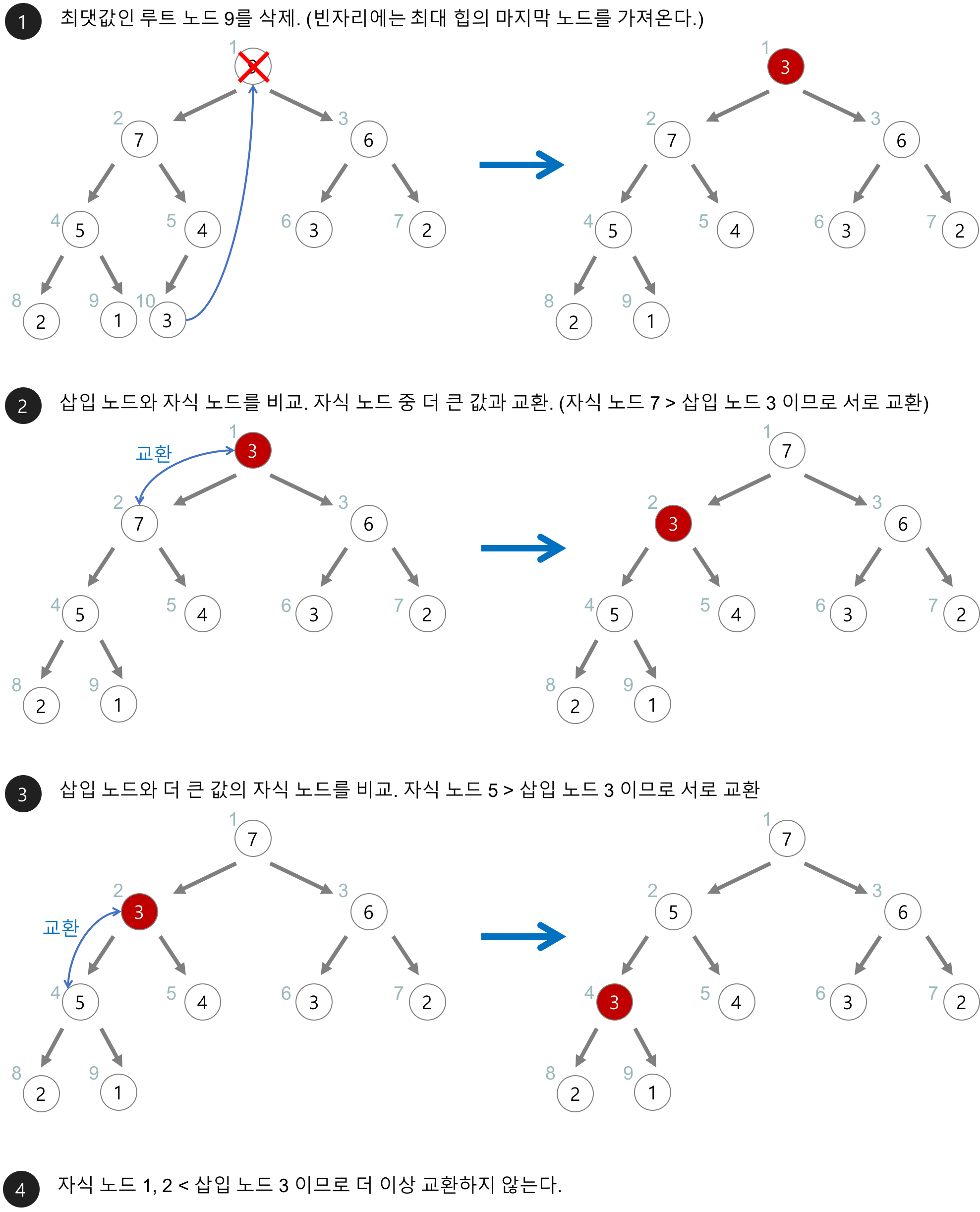
위처럼 기존 루트 노드 값 9 을 삭제하는 경우, 기존의 3 을 루트로 가져와 자식 노드와 비교하면 순차적으로 내려가게 됩니다.
1-2. Min Heap
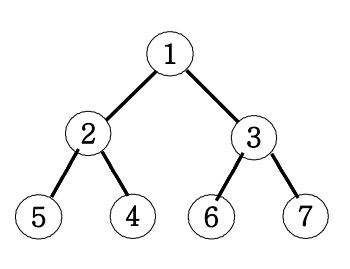
최소 힙의 다른 점은 자식 노드의 값이 부모 노드 값보다 항상 크거나 같습니다.
또한 데이터 추출 시 제일 작은 데이터가 가장 먼저 나오게 됩니다.
(1) 삽입
-
최소 힙에 새로운 데이터가 들어오면 일단 리프 노드 마지막에 이어서 삽입합니다.
-
이후 부모 노드의 값과 비교하면서 최대 힙의 구조를 만족하도록 자리를 변경합니다.
예시를 보도록 하겠습니다.
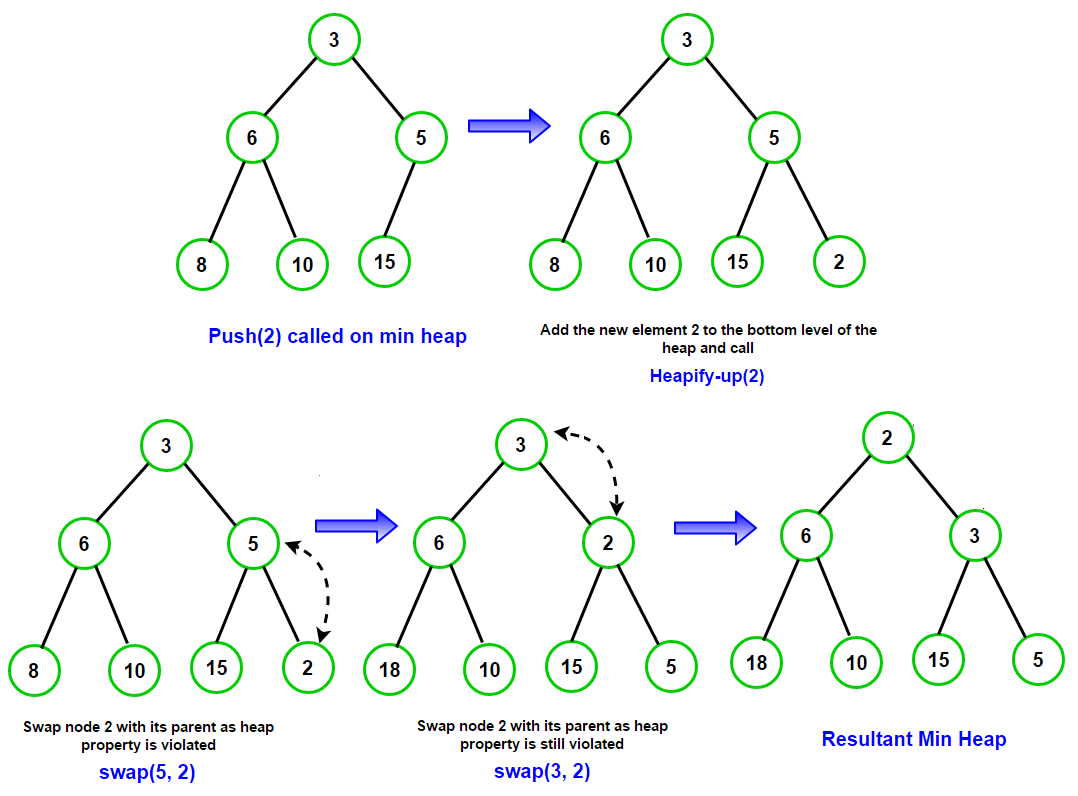
위처럼 새로운 값 2 을 삽입하는 경우, 가장 마지막에 위치하고 기존의 3보다 작은 값이기 때문에 부모노드와 비교하며 순차적으로 올라오게 됩니다.
(2) 삭제
-
최소 힙에서 데이터를 꺼내는 경우 가장 작은 데이터를 꺼내는 것이므로 루트 노드가 삭제됩니다.
-
삭제된 루트 노드 자리에 리프 노드의 가장 마지막 데이터를 가져옵니다.
-
이후 자식 노드의 값과 비교하면서 최소 힙의 구조를 만족하도록 자리를 변경합니다.
예시를 보도록 하겠습니다.
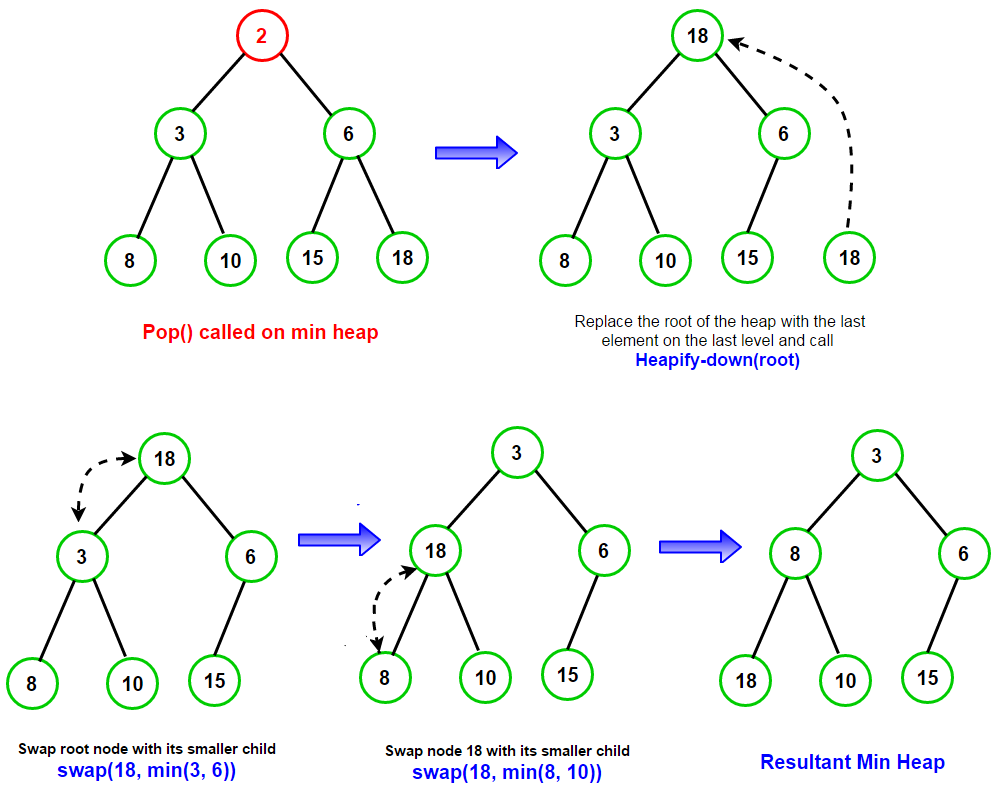
위처럼 기존 루트 노드 값 2 을 삭제하는 경우, 기존의 18 을 루트 노드로 가져와 자식 노드와 비교하면 순차적으로 내려가게 됩니다.
2. 장단점
장점
-
데이터에 우선순위를 부여해 빠르게 접근할 수 있습니다.
-
데이터의 정렬에 효과적입니다. (Heap Sort)
-
삽입과 삭제, 정렬 모두
O(logN)의 시간 복잡도를 가집니다.
앞서 말씀드린 배열과 연결리스트로 구현하지 않는 이유를 이제 알 수 있습니다.
힙으로 우선순위 큐를 구현하는 경우 삽입과 삭제 과정 모두 ‘부모 노드’ 와 ‘자식 노드’ 간의 비교만 이루어집니다.
또한 완전이진트리 형태를 가지고 있기 때문에 높이(Depth)가 하나 증가 시 저장 가능한 데이터는 2배, 비교 연산 횟수는 1회 증가합니다.
결론적으로 최악의 경우에도 삽입과 삭제 모두 O(logN)의 시간 복잡도를 가집니다.
조금 이해가 되셨나요?
단점
- 완전이진트리를 기반으로 하기 때문에 구현이 조금 복잡할 수 있습니다.
3. 구현
자바와 파이썬에서 힙을 사용해보도록 하겠습니다.
3-1. Java
자바에서는 Heap을 PriorityQueue클래스를 사용해서 구현할 수 있습니다.
또한 배열을 통해서 우선순위 큐를 구현하고 있습니다!
엣 배열이요??? 분명 배열로 구현하면 효율성이 떨어진다고 하지 않았나요??
그래서 배열의 장점인 인덱스를 통해 트리형태로 구현하고 있습니다
-
왼쪽 자식 노드 인덱스 = 부모 노드 인덱스 × 2
-
오른쪽 자식 노드 인덱스 = 부모 노드 인덱스 × 2 + 1
-
부모 노드 인덱스 = 자식 노드 인덱스 / 2
또한 자바의 PriorityQueue 클래스는 Queue 인터페이스를 구현하고 있습니다.
따라서 큐에서 사용했던 메소드를 동일하게 사용할 수 있습니다.
add(E e)offer(E e)peek()remove()
한 번 사용해보도록 하겠습니다.
//우선순위 큐 선언 -> 최소 힙
PriorityQueue heap = new PriorityQueue();
heap.add(3);
heap.offer(1);
heap.offer(5);
heap.add(33);
int peek = (int) heap.peek(); // 출력 -> 1
//우선순위 큐 선언 -> 최대 힙
PriorityQueue heap2 = new PriorityQueue(Comparator.reverseOrder());
heap2.add(3);
heap2.offer(1);
heap2.offer(5);
heap2.add(33);
int peek = (int) heap.remove(); //출력 -> 33위와같이 비교연산자를 넣어줌으로써 최소 힙과 최대 힙 각각으로 사용할 수 있습니다.
그렇다면 정말 앞서 말했던 인덱스 규칙에 따라 구현되고 있는지 내부적으로 한 번 살펴보겠습니다.
offer()는 아래와 같이 구현되어 있습니다.
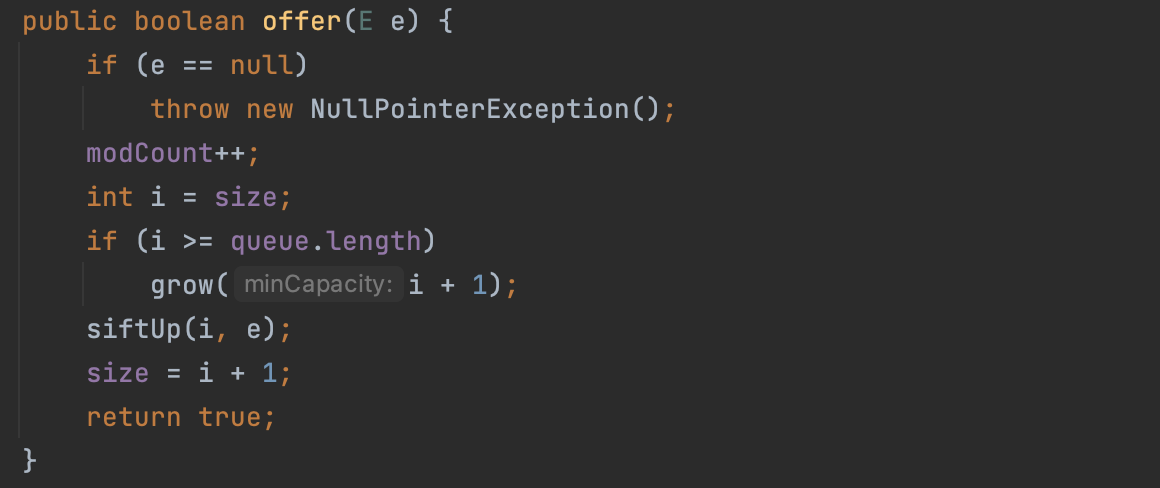
스택처럼 배열의 기본 용량을 넘어가면 grow() 를 통해 배열의 용량을 확장시키는 것을 확인할 수 있습니다.
중요한 것은 그 아래에 siftUp(i, e) 입니다.

해당 함수가 실질적으로 요소가 들어왔을 때 비교하는 함수입니다.
비교연산자의 여부에 따라 두가지로 갈라지는 것을 확인 할 수 있습니다.
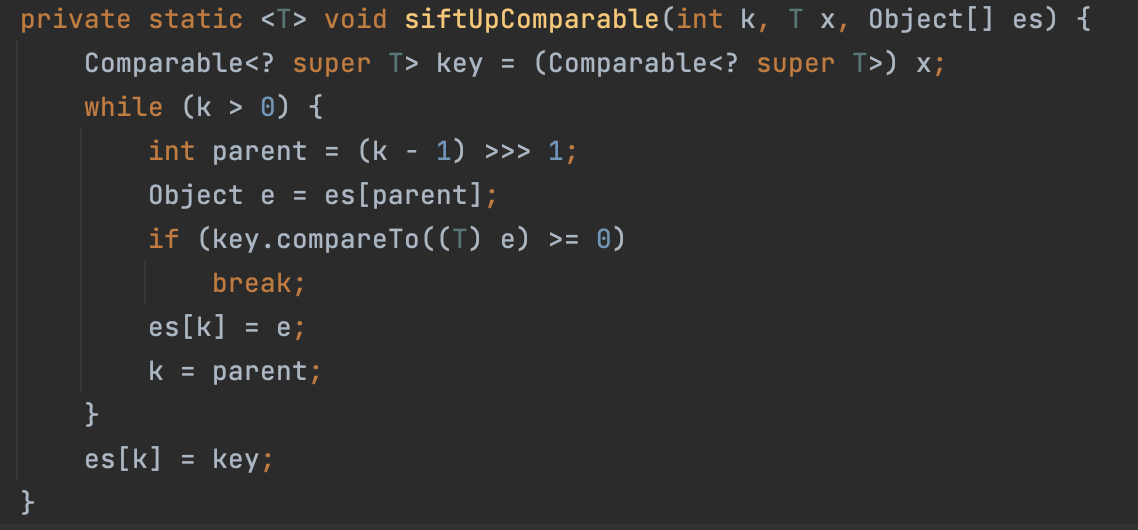
비교 연산자가 없는 경우 위 메소드를 통해 요소 값을 비교하고 있습니다.
핵심은 >>> 을 통해 부모 노드의 값을 가져오는 부분입니다.
즉, 부모 노드 인덱스 = 자식 노드 인덱스 / 2을 수행하여 부모와 비교하고 있습니다.
어떠신가요? 조금 이해가 되셨나요??
흥미롭지 않나요?ㅎㅎ
3-2. Python
파이썬은 heapq 모듈을 통해 힙을 사용할 수 있습니다.
사용할 수 있는 메소드는 아래와 같습니다.
-
heapq.heappush(heap, x)- 힙에 데이터 삽입 -
heapq.heappop(heap)- 힙에서 가장 작은 데이터 추출 -
heapq.heapify()- 힙 형태로 재정렬
역시나 파이썬답게 심플합니다.
한 번 사용해보도록 하겠습니다.
# heapq 모듈
import heapq
heap = []
# 데이터 삽입
heapq.heappush(heap, 5)
heapq.heappush(heap, 1)
heapq.heappush(heap, 7)
first = heapq.heappop(heap) # 출력 -> 1
list = [3, 1, 6]
heapq.heapify(list)
first = heapq.heappop(list) # 출력 -> 1파이썬은 따로 최소 힙을 기본으로 제공하고, 최대 힙은 따로 구현하지 않고 있습니다.
최대 힙처럼 사용하기 위해선 데이터 삽입 시 음수로 넣어야 합니다.
# heapq 모듈
import heapq
heap = []
# 데이터 삽입
heapq.heappush(heap, -5)
heapq.heappush(heap, -1)
heapq.heappush(heap, -7)
first = -heapq.heappop(heap) # 출력 -> 7참 쉽죠?
힙에 대해서 관련 개념과 장단점, 자바와 파이썬에서의 구현까지 쭉 정리해보았습니다!
잘 따라오셨나요?.?
하나라도 도움이 되는 내용이었으면 좋겠습니다 ㅎㅎ
오늘도 읽어주셔서 감사합니다!❤️
References
자료구조 - 우선순위 큐(Priority Queue)와 힙(heap)
[자료구조] 힙(heap) - 최대힙(max heap)의 삽입과 삭제