Functional Dependency
X 속성의 값에 따라 Y 속성의 값이 결정. = X 속성이 Y 속성을 함수적으로 결정한다라고 한다. X의 값이 같을 때 Y값도 같은지를 확인하면 된다.
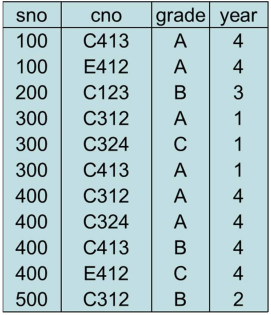
여기서의 FD는 sno와 year 사이에 있다고 할 수 있다. 이러한 관계를 X -> Y = Y is functionally dependent on X.
- X는 결정자이고, Y는 X에 종속된다
- 두 개의 튜플의 X속성이 동일한 값을 가질 때, 이 튜플의 Y속성의 값도 동일해야 함.
- X가 relation 의 key 라면, X->Y 다른 속성 결정.
- ✅ 위 테이블에서 sno, cno가 primary key 이므로 (조합이므로) sno, cno 가 같다면 -> grade 가 같아야 하고, sno, cno 가 같다면 year 이 같아야 한다.
Functional Dependency Diagram

- 추가로 다른 함수 종속 sno -> year 을 찾을 수 있다.
종속 다이어그램은 다음과 같다.
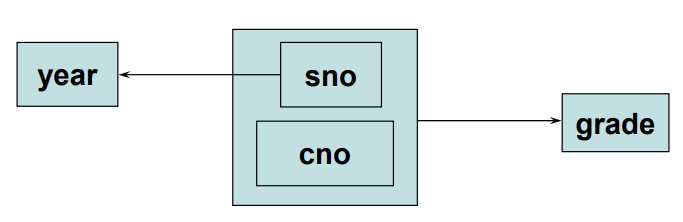
{sno, cno} -> year 화살표는 필요가 없다. primary의 member(sno)가 누군가(year)의 결정자라면 당연히 조합에서 year의 결정자였기 때문에 표시하지 않아도 된다. (명시적으로 내포)
함수 종속을 파악해보자
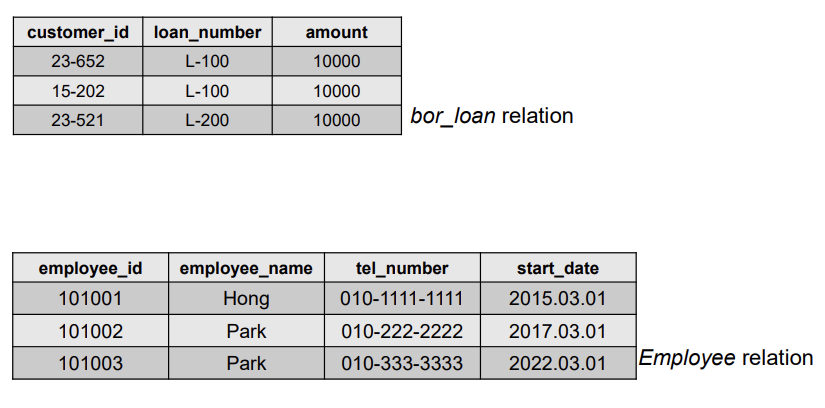
- 먼저 primary key 를 파악해야 한다. 어떤 고객이 2개 이상이 된다면 {customer_id, loan_number} 가 될 것이고, 아니면 {customer_id}
bor_loan :
박스 안에는 customer_id만.
customer_id -> loan_number
customer_id -> amount
loan_number -> amount
or
{customer_id, loan_number} -> amount 이고, 박스 안 loan_number 에서만 화살표.
Employee relation :
employee_id -> employee_name,
employee_id -> tell_number,
employee_id -> start_date
개별 직원마다 tel_number 가 다르다면 name, start_date 을 결정할 수도.
Full FD and Partial FD
-
이전에는 total 과 partial 이었다.
-
primary key 가 여러 개일때 X,Y 관계는 full , partial 일 수 있다.
-
Full
: X가 두 개 이상 속성, X' 가 X 하위일 때 X'-> Y가 성립 안하는 경우 (개별 멤버는 성립 안함) -
Partial
: 하위 속성 X' 에 대해 X' -> Y가 성립하는 경우 x-> Y 는 부분 함수 종속

- full 입니댜
- full
- partial
How to solve anomaly?
anomaly 있다 -> 테이블의 사이즈를 줄여야 한다 -> 테이블을 쪼개자 (decompose) -> Normalization
-
1NF
-
2NF
-
3NF
-
BCNF
-
4NF
-
5NF
-
정규형마다 조건이 있으며, 이를 이해해야 한다.
1NF
조건: 모든 도메인이 원자값으로만 구성, composite att, multi-valued att 는 안됨.
non-atomic 값을 제거하는 것이 1NF 이다.
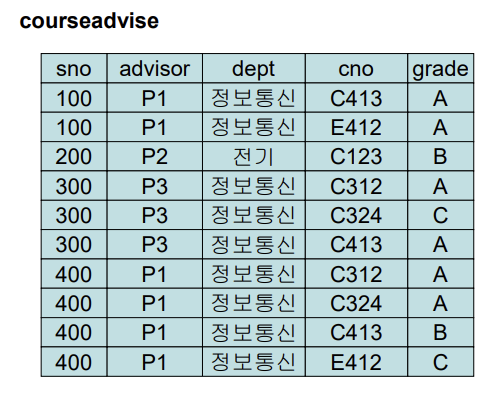
- 정보를 유지하면서 삭제해야 한다.
- 튜플 추가하여 수평적 분할(튜플 추가), att 단위 수직적 분할(att 추가)이 가능하다.
- 튜플을 추가하면 id (primary key) 가 중복되어 키를 바꿔야 한다(이럴 경우 primary key 를 id + tel_num 으로 할 수 있다)
- att 를 분할할 경우 다른 id 에 대해 null 값이 생긴다.
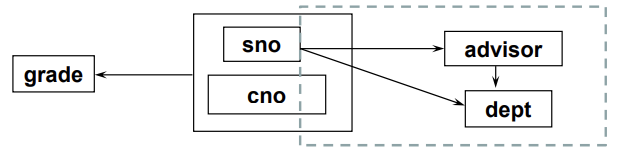
{sno, cno} > grade
{sno, cno} > advisor
{sno, cno} > dept
sno > advisor
sno > dept
advisor > dep
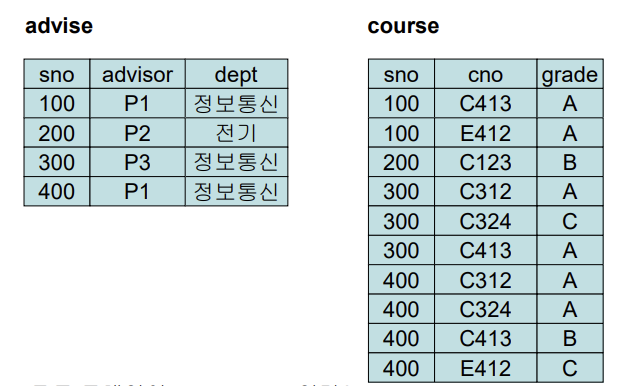
- atomic value 만 있으모로 1NF 이다
- 그다음 anomaly 를 본다
- cno 는 null 을 허용하지 않으므로 sno가 500인 정보를 수강과목 없이 추가할 수 없다.
- sno 200인 학생의 cno 정보를 삭제하면 advisor, dept, advior의 학과 모두 삭제된다.
- sno 400 의 advisor 가 P3 로 바뀌면 모두 바뀌지 않으면 anomaly.
: 기본키에 부분함수 종속이 발생하여 문제가 생긴다. 이를 2NF 에서 해결.

{sno, cno} > advisor, {sno, cno} > dept 가 부분함수 종속이라 문제! 이걸 제거하자.
sno 는 advisor와 dept 의 결정자인 것이 맞다(상식적으로 생각해도.) grade 도 그러하므로 grade, cno, sno 를 하나로 묶고 sno, advisor, dept 를 하나로 묶은 2개의 테이블을 만들자.
2NF
조건: 1정규형 요건은 기본으로 충족, prime att 제외 모든 att가 기본키에 완전 종속된 상태.
즉 부분함수 종속이 모두 제거되도록 한다.
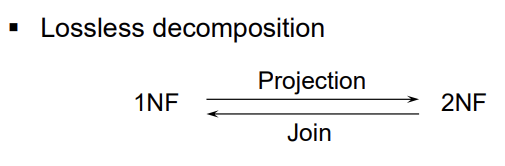
- Projection 은 수직적으로 쪼개는 것, Join 을 다시 해도 원래 테이블의 정보가 유지되어야 함.
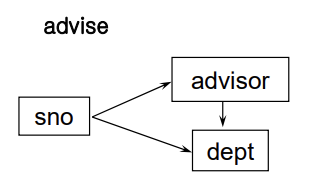
- 외래키 = 두 테이블의 관계를 설정해주는 sno
- 둘 중에서도 primary key가 sno 인 테이블(advise)의 sno가 main 키가 된다.

- 모든 도메인이 원자값이다
- 부분 함수 종속이 해결되었다
- 2정규형이라 할 수 있다
- 다시 anomaly 분석해본다 (이번엔 각 테이블에 대해 다 한다)
advise
1. Insertion 있음(500을 추가하고 싶은데 지도교수 P4를 학과 정보 없이 추가를 못한다. dependency 가 있어서) 2. deletion 있음(200지우면 P2의 학과가 전기라는 정보 삭제됨, 300도) 3. P1의 학과가 정보통신에서 정보로 바뀌면 P1을 모두 찾아 바꿔야 함
course
1. Insertion 없음(primary key 라 무조건 null 값 없이 추가) 2. deletion 없음(200을 지우면 튜플을 완전히 삭제하는데 문제가 없다.) 3. Update 없음(sno, cno 에서 중복된 튜플이 없어서)
: Transitive FD 때문에 anomaly 가 발생한다.
X > Y, Y > Z, X > Z 와 같은 관계가 있다면 이를 Transitive FD 라 한다.
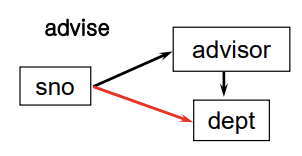
이를 제거하는 것이 3정규형이다.
3NF
: 2정규형 충족, att 간 이행적 종속이 없는 상태.
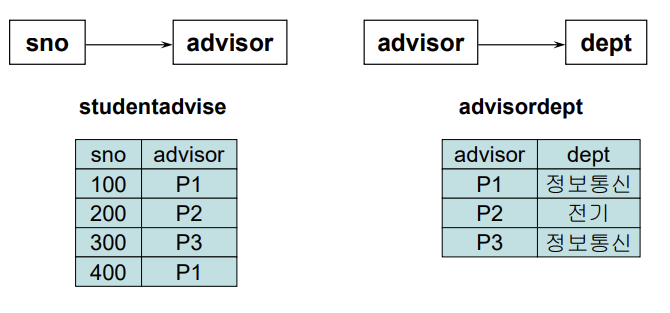
- att 가 두 개인 테이블은 무조건 3NF
- X가 primary, Y가 후보키이면 anomaly 발생하지 않음. (후보키라면 유일성 만족해야 함, 위의 경우는 아니었다.)
- 그건 왜 그럴까?
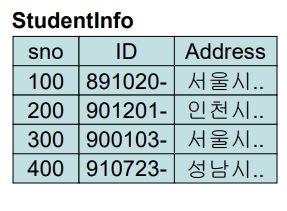
sno > ID
ID > Address
sno > Address
Primary key 는 sno, ID 가 후보키이다.
- 2정규형이라 봐야한다.
- insertion 무시(학번을 null로 하며 다른 정보를 넣을 필요가 없다.) 2. deletion 무시(연쇄 삭제는 되지만 꼭 필요한 정보가 아니므로 무시) 3. update 없음 (ID가 후보키이므로 일괄 업데이트 정보가 없다.)
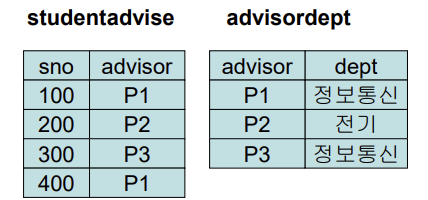
어떤 att 를 공통으로 해서 나눌까?
- sno, advisor와 sno, dept 로 나누면 advisor의 dept 정보가 사라진다.
- advisor, sno 와 advisor와 dept 로 나누면 된다. Y를 매개로 하는 게 정석!
studentadvise 의 advisor > advisoradapt 의 advisor (화살표)
- 당연 해결.
- 300을 삭제하면 왼쪽에서만 삭제, 연쇄 삭제 X.
- 오른쪽에서만 P1 소속학과만 업데이트 해주면 된다.