로지스틱 회귀분석

로지스틱 함수에서 이직 분류 문제를 풀기위해 발전되었다
이 모델은 주로 예/아니오, 성공/실패와 같이 두 가지 범주로 결과가 나뉘는 경우에 사용

• 확률추청 : 로지스틱 회귀는 주어진 데이터가 특정 클래스에 속할 확률을 추청
  이 확률은 0과 1 사이의 값으로, 예측된 확률이 특정 임계값(보통 0.5)이상이면 하나의 클래스로, 이하면 다른 클래스로 분류

• 시그모이드 함수 : 로지스틱 회귀는 시그모이드 함수(또는 로지스틱 함수)를 사용하여 입력 데이터의 선형 조합을 0과 1사이의 확률값으로 변환

• 최대 우도 추정 : 로지스틱 회귀 모델은 최대 우도 추정(Maximum Likelihood Estimation, MLE) 방법을 사용하여 모델 파라미터를 추정. 이는 주어진 데이터에 대해 관측된 결과의 확률을 최대화하는 파라미터 값을 찾는 과정

• 이진 분류 : 로지스틱 회귀는 기본적으로 이진 분류를 위해 설계되었지만, 원-대-다(One-Vs-Rest)방식이나 원-대-원(One-vs-One) 방식을 통해 다중 클래스 분류 문제에도 적용

언제 사용하면 좋을까?

로지스틱 회귀분석은 주로 이진분류 문제를 해결하기 위해 사용
이는 결과가 두가지 범주(예/아니오,성공/실패) 중 하나로 나누어지는 경우에 적합
주로 데이터 수가 많지 않은 경우 간단한 모델이 필요할 때 사용
또한, 분석결과에 대한 설명과 해석이 중요할때 사용하면 좋다

장점

1. 해석 용이성 : 로지스틱 회귀 모델은 결과를 해석하기 쉽습니다.
   각 특성의 가중치를 분석하여 어떤 특성이 결과에 더 큰 영향을 미치는지 이해할 수 있습니다
2. 확률 추청 : 결과의 확률을 제공하여, 단순한 분류뿐만 아니라 결과의 불확실성을 평가할 수 있습니다
3. 유연성 : 다른 회귀 모델과 마찬가지로 다양한 유형의 데이터에 적용할 수 있으며, 커널 방법 등을 사용해 비선형 관계를 모델링할 수도 있습니다.

한계점

1. 비선형 관계의 제한적 모델링 : 로지스틱 회귀는 기본적으로 선형 관계를 가정한다. 복잡한 비선형 관계를 모델링하기 위해서는 추가적인 기법이 필요하다.
2. 특성 선택의 중요성 : 중요하지 않거나 상관관계가 높은 특성이 포함괴어 있으면 모델의 성능이 저하될 수 있다.
3. 과적합의 위험성 : 특성의 수가 많거나 모델이 복잡할 경우 과적합이 발생할 수 있으며 이를 피하기 위해 적절한 규제가 필요하다.

로지스틱 회귀분석 이론

오즈(Odds) : 특정 사건이 발생할 확률과 그 사건이 발생하지 않을 확률 간의 비율

예를들자면, 어떤 사건의 발생 확률이 0.75라고 가정해보면
이 경우, 이 사건이 발생하지 않을 확률은 0.25가 된다.
그러면 이 사건의 오즈는 다음과 같이 계산된다.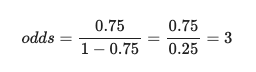
이것은 사건이 발생할 확률이 발생하지 않을 확률보다 3배 높다는것을 의미

로그변환 : 로지스틱 회귀에서는 종속 변수의 로그 오즈(log odds)를 독립변수들의 선형 조합으로 모델링한다. 즉, 로지스틱 회귀는 확률을 직접 모델링하지 않고, 오즈를 로그 변환하여 사용. 오즈는 0이상의 값만 존재하지만, 로그변환을 하면 값의 범위가 실수 전체로 확장되어, 종속변수와 독립변수 사이의 관계를 선형방정식으로 표현할 수 있습니다. 로그 오즈는 다음과 같이 정의된다.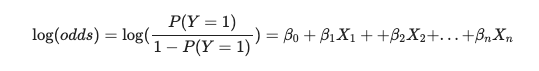
이 식에서 각각의 요소는 다음과 같은 의미

• β0,β1,β2,β3..., βn은 모델의 계수(가중치)입니다. 이들은 각 독립 변수가 종속 변수에 미치는 영향의 크기를 나타낸다
• X1,X2,...,Xn 은 독립 변수(설명 변수)입니다. 이들은 분석 대상이 되는 데이터의 특성을 나타낸다.