이번 장에서 우리는 키-값 저장소를 설계한다.
키-값 저장소는 키-값 데이터베이스라고도 불리는 비 관계형 데이터베이스이다.
이 저장소에 저장되는 값은 고유 식별자를 키로 가져야한다. 키와 값 사이의 이런 연결 관계를 "키-값" 쌍이라고 지칭한다.
- 키는 유일해야한다
- 값은 키를 통해서만 접근할 수 있다.
- 키는 일반 텍스트일 수도 있고 해시값일 수도 있다.
- 성능 상의 이유로, 키는 짧을 수록 좋다.
- 값은 문자열일수도, 리스트일수도, 객체일 수도 있다.
- ex) 아마존 다이나모, memcached, 레디스 등이 있다.
우리가 설계해야하는 키-값 저장소는 다음 연산을 지원한다.
put(key, value): 키-값 쌍을 저장소에 저장한다.get(key): 인자로 주어진 키에 메달린 값을 꺼낸다.
문제 이해 및 설계 범위 확정
우리가 결정해야할 것은 다음의 것들이 있다.
- 읽기, 쓰기, 메모리 사용량 사이의 균형
- 데이터의 일관성(consistency)와 가용성(availability)에서의 타협적결정
그리고 이것을 결정하기 위해 다음의 특성을 알고 있다.
- 키=값 쌍의 크기는 10KB 이하이다.
- 큰 데이터를 저장할 수 있어야 한다.
- 높은 가용성 (👉🏻 장애 상황에서도 빠르게 응답해야한다.)
- 높은 규모 확장성 (👉🏻 트래픽 양에 따라 자동적으로 서버 증설/삭제가 이뤄져야한다.)
- 데이터 일관성 수준은 조정이 가능해야한다
- 응답 지연시간이 짧아야한다.
단일 저장소
가장 직관적인 방법은 키-값 쌍 전부를 메모리에 해시테이블로 저장하는 것이다. 단일 저장소인 것이다.
빠른 속도를 보장하긴 하지만, 모든 데이터를 한 메모리 안에 두는 것이 불가능할 수도 있다.
이에 대한 개선책으로
- 데이터 압축 (compression)
- 자주쓰이는 데이터만 메모리에 두고 나머지는 디스크에 저장
을 사용할 수 있다.
하지만 우리 문제의 요구사항 중
큰 데이터를 저장할 수 있어야 한다. (데이터를 저장하는 총 용량이 커야함)
높은 가용성 (단일 장애 지점이 되면 안된다)
높은 규모 확장성 (트래픽의 양이 많아져도 성능을 유지할 수 있어야한다)
들을 고려해보았을 때, 분산 키-값 저장소로 설계하는 것이 맞아보인다.
분산 키-값 저장소
분산 해시 테이블이라고도 불린다. 분산 시스템을 설계할 때는 CAP 정리를 이해하고 있어야한다.
CAP 정리
CAP 정리는
- consistency: 분산 시스템에 접속하는 모든 클라이언트는 어떤 노드에 접속했느냐와 관계없이 언제나 같은 데이터를 보게 되어야 한다.
- availability: 분산 시스템에 접속하는 클라이언트는 일부 노드에 장애가 발생하더라도 항상 응답을 받을 수 있어야 한다.
- partition tolerance: 파티션은 두 노드 사이에 통신 장애가 발생하였음을 의미한다. 파티션 감내는 네트워크에 파티션이 생기더라도 시스템은 계속 동작하여야 한다는 것을 뜻한다.
(분할된 네트워크 환경에서 동작하는 시스템에서 두 네트워크가 단절되거나 네트워크 데이터의 유실이 일어나더라도 각 지역 내의 시스템은 정상적으로 동작해야 함이랑 같은 말)
이 세 가지 요구 사항을 동시에 만족하는 분산 시스템을 설계하는 것이 불가능하다라는 정리다.
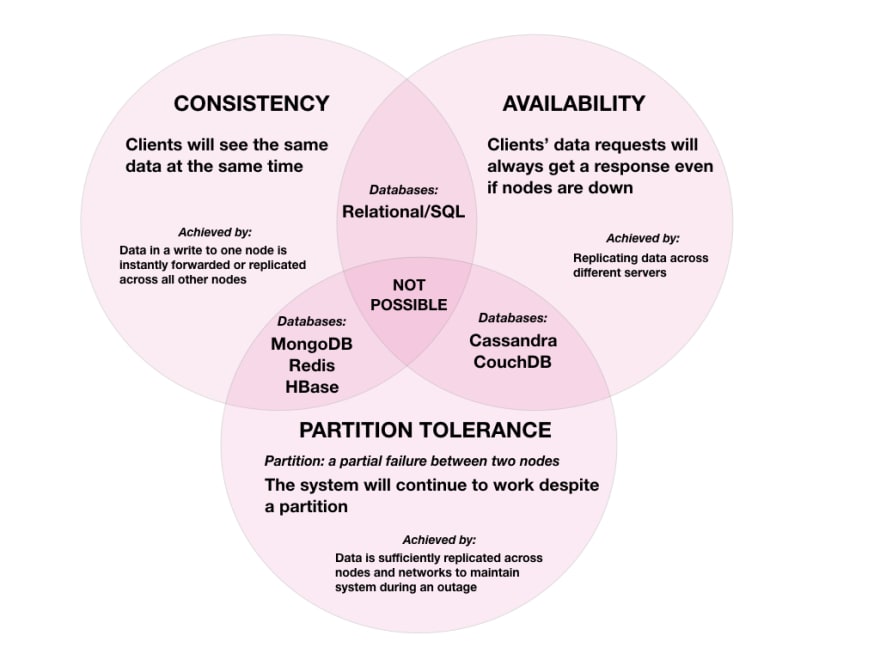
키-값 저장소는 세 가지 요구사항 가운데 어느 것을 만족하냐에 따라 분류할 수 있다.
- CP 시스템: 일관성, 파티션 감내를 지원
- AP 시스템: 가용성과 파티션 감내를 지원
- CA 시스템: 일관성과 가용성을 지원하는 저장소. 실제로 존재하지 않음
CAP 정리의 정의를 다시 이해해보기
C,A,P가 모두 분산시스템의 특성에 대한 것으로 여겨지지만, 실상은 그렇지 않다. 앞에서 언급한 정의를 생각해본다면, C와 A는 분산시스템의 특성이지만, P는 그 분산시스템이 돌아가는 네트워크에 대한 특성이다.
...
P의 정의는 네트워크가 임의의 메시지 손실을 할 수 있다는 것을 허용하느냐이다. 다시 말해 네트워크가 가끔 장애가 날 수 있다는 것을 인정하느냐는 것이다. P의 선택을 배제하려면, 절대로 장애가 나지 않는 네트워크를 구성해야 하지만 그런 것은 이 세상에 존재하지 않는다. 따라서 원하든 원하지 않든 P는 선택되어야 하며 결국 선택권은 C나 A중 하나밖에 없다.
이상적 상태
이상적 환경이라면 네트워크가 파티션되는 상황은 절대로 일어나지 않을 것이다. n1에 기록된 데이터는 자동적으로 n2와 n3에 복제된다. 데이터 일관성과 가용성도 만족된다.
그러나 실제는 다르다
분산시스템은 파티션 문제를 피할 수 없다. 파티션 문제가 발생하면 우리는 일관성과 가용성 사이에서 하나를 택해야한다.
n3에 장애가 발생한 상황. 클라이언트가 n1이나 n2에 쓰기 연산을 하면 n3에는 전달되지 않는다. 반대의 경우도 마찬가지. 서로가 오래된 사본을 가지게 될 수 있다.
-
일관성을 택한다면?
: n1과 n2에 대해서도 쓰기연산을 중단시킨다. -
가용성을 택한다면?
: 계속 읽기 연산을 허용해야한다. n1, n2에서의 쓰기연산도 허용할 것이다. 파티션 문제가 해결되면 새 데이터를 n3에 전송할 것이다.
면접 문제의 요구사항에 따라 CAP 정리를 적절히 적용하자~
시스템 컴포넌트
이번 절에서는 키-값 저장소 구현에 사용될 핵심 컴포넌트들 및 기술들을 살펴볼 것이다.
데이터 파티션
대규모의 애플리케이션의 경우, 전체 데이터를 작은 파티션으로 분할한 다음 여러대의 서버에 저장해야한다.
데이터를 파티션 단위로 나눌 때 다음 문제를 해결해야한다.
- 데이터를 여러 서버에 고르게 분산할 수 있는가
- 노드가 추가되거나 삭제될 때 데이터의 이동을 최소화할 수 있는가
5장에서의 안정해시가 이 문제에 적합한 해결책이된다.
데이터 다중화
고가용성과 안정성을 확보하려면 비동기적인 다중화가 필요하다.
다중화할 서버를 선정하는 방식은 다음과 같다!
해시 링 위에 저장할 키 값을 배치하고 만나는 N개의 서버에 데이터 사본을 보관하는 것이다.
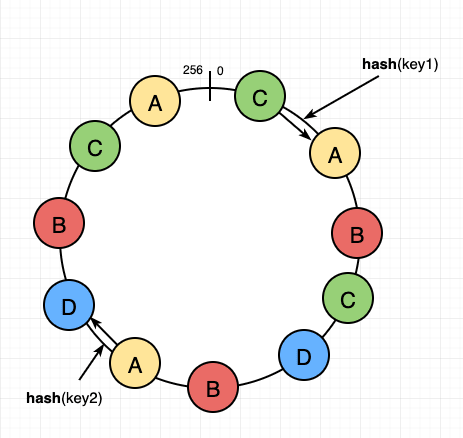
근데 가상 노드를 사용한다면 같이 선택한 N개의 노드가 대응될 실제 물리 서버의 개수가 N보다 작아질 수 있다. 같은 물리서버를 중복 선택하지 않도록 해야한다.
데이터 일관성
여러 노드에 다중화된 데이터는 적절히 동기화가 되어야한다.
정족수 합의 프로토콜
- N: 사본 개수
- W: 쓰기 연산에 대한 정족수, 적어도 W개의 서버로부터 성공했다는 응답을 받아야한다.
- R: 읽기 연산에 대한 정족수, 적어도 R개의 서버로부터 성공했다는 응답을 받아야한다.
W, R, N의 값을 정하는 것은 응답 지연과 데이터 일관성 사이의 타협점을 찾는 전형적인 과정이다.
W, R이 작은 경우 응답속도는 빠를 것이다. W,R이 큰 경우는 데이터 일관성 수준은 향상되지만 응답은 느려질 것이다.
보통 요구 사항에 따라 N, W, R을 다음처럼 정할 수 있다.
- 빠른 읽기 연산에 최적화된 시스템: R=1, W=N
- 빠른 쓰기 연산에 최적화된 시스템: W=1, R=N
- 강한 일관성이 보장됨: W + R > N
- 강한 일관성이 보장되지 않음: W + R <= N
일관성 모델
일관성 모델은 데이터의 일관성의 수준을 결정하는데, 종류가 다양하다.
- 강한 일관성: 모든 읽기 연산은 가장 최근에 갱신된 결과를 반환한다. 다시 말해서 클라이언트는 절대로 낡은 데이터(out-of-date)를 보지 못한다.
- 약한 일관성(weak consistency): 읽기 연산은 가장 최근에 갱신된 결과를 반환하지 못할 수 있다
- 최종 일관성: 약한일관성에 속함. 갱신 결과가 모든 사본에 반영이 되는 모델
이번 장에서는 최종 일관성 모델을 따를 것.
비 일관성 해소 기법: 데이터 버저닝
최종 일관성 모델을 따를 경우 일관성이 깨질 수 있다.
이 문제는 클라이언트가 해결해야하는데, 이 때 versioning과 vector clock을 사용한다.
버저닝은 데이터 변경 시마다 데이터의 새로운 버전을 만드는 것이다. 각 버전의 데이터는 불변하다
서버 1, 2가 있고 두 서버가 같은 키 값에 대해 다른 버전의 데이터를 가지고 있다면, 이 둘의 충돌을 어떻게 해결해야할까?
바로 벡터 시계를 이용하는 것이다.
벡터 시계는 [서버, 버전]의 순서쌍을 데이터에 메단것이다. 어떤 버전이 선행 버전인지, 후행 버전인지, 아니면 다른 버전과 충돌이 있는지 판별하는데 쓰인다.
추상적 로직
-
클라이언트가 데이터 D1을 시스템에 기록한다. 이 쓰기 연산을 처리한 서버는 Sx이다. 따라서 벡터 시계는 D1([Sx, 1])으로 변한다.
-
다른 클라이언트가 데이터 D1을 읽고 D2로 업데이트한 다음 기록한다. D2는 D1에 대한 변경이므로 D1을 덮어쓴다. 이 때 쓰기 연산은 같은 서버 Sx가 처리한다고 가정하자. 벡터 시계는 D2([Sx, 2])로 바뀔 것이다.
-
다른 클라이언트가 D2를 읽어 D3로 갱신한 다음 기록한다. 이 쓰기 요청은 Sy가 처리한다고 가정하면 벡터시계는 D3([Sx, 2], [Sy, 1])로 바뀐다.
-
Sy가 요청을 처리하기 전에 또 다른 클라이언트가 D2를 읽고 D4로 갱신한 다음 기록한다. 이때 쓰기연산은 서버 Sz가 처리한다고 가정하자. 그러면 벡터시계는 D4([Sx, 2], [Sz, 1])이 된다.
-
어떤 클라이언트가 D3와 D4를 읽으면 데이터 간 충돌이 있다는 것을 알게된다.
D3(\[Sx, 2], \[Sy, 1])
D4(\[Sx, 2], \[Sz, 1])이런 경우, 클라이언트가 해소한 후에 서버에 기록한다. 이 쓰기 연산을 처리한 서버가 Sx였다고 하면, 벡터시계는 D5([Sx, 3], [Sy, 1], [Sz, 1])로 바뀐다.
충돌 감지
어떤 버전 X와 Y 사이에 충돌이 있는지 보려면 Y의 벡터 시계 구성요소 가운데 X의 벡터 시계 동일 서버 구성요소보다 작은 값을 갖는 것이 있는지 보면 된다.
+) 벡터 클락 충돌 해소
- Last Write Wins (LWW)
: timestamp에 기반해서 저장소가 충돌 해결을 하는 것이 고려될 수 있다. (ex. riak, voldemort) 데이터에 버전벡터와 함께 타임스탬프도 저장이 된다.
벡터 시계의 단점
- 앞서 봤던 것처럼 그들은 충돌을 "감지"할 수만 있다. 충돌 해소를 위해서는 lww같은 옵션이 추가되거나 대체된다.
- 버전 벡터 노드 수가 늘어남에 따라 연산에 드는 비용도 늘어난다. 노드 수가 몇 만 이상이 되면 저장공간의 문제도 생긴다.
장애 처리
대다수 대규모 시스템에서 장애는 그저 불가피하기만 한 것이 아니라 아주 흔하게 벌어지는 사건이다. 따라서 장애를 어떻게 처리할 것이냐 하는 것은 굉장히 중요한 문제다. 이번 절에서 우리는 우선 장애 감지 기법들을 먼저 살펴보고, 그 다음으로 장애 해소 전략들을 짚어 볼 것이다.
장애 감지
분산 시스템에서는 보통 두 대 이상의 서버가 서버 A의 장애를 보고해야 해당 서버에 실제로 장애가 발생했다고 간주하게 된다.
- 모든 노드 사이에 멀티캐스팅 채널을 구축하는 것이 서버 장애를 감지하는 가장 손쉬운 방법이다. 하지만 서버의 수가 많아진다면 비효율적일 것이다.
가십 프로토콜 (gossip protocol)
동작원리
- 각 노드는 멤버십 목록을 유지한다. 멤버십 목록은
각 멤버 ID, 박동 카운터쌍의 목록이다. - 각 노드는 주기적으로 자신의 박동카운터를 증가시킨다.
- 각 노드는 무작위로 선정된 노드들에게 주기적으로 자기 박동 카운터 목록을 보낸다.
- 박동 카운터 목록을 받은 노드는 멤버십 목록을 최신값으로 갱신한다.
- 어떤 멤버의 박동 카운터 값이 지정된 시간동안 갱신되지 않으면 해당 멤버는 장애 상태인 것으로 간주된다. (아무 서버도 해당 서버에게서 리스트를 전달받지 못했다는 뜻)
일시적으로 장애를 처리하는 법
가십 프로토콜로 장애를 감지한 시스템은 가용성을 보장하기 위해 필요한 조치를 해야한다. 엄격한 정족수 접근법을 쓴다면 앞서 "데이터 일관성" 절에서 설명한 대로, 읽기와 쓰기 연산을 금지해야 할것이다.
느슨한 정족수 접근법은 이 조건을 완화하여 가용성을 높인다. 정족수 접근법은 이 조건을 완화하여 가용성을 높인다. 정족수 요구사항을 강제하는 대신, 쓰기 연산을 수행할 W개의 건강한 서버와 읽기 연산을 수행할 R개의 건강한 서버를 해시 링에서 고른다. 이때 장애 상태의 서버는 무시한다.
네트워크나 서버 문제로 장애 상태인 서버로 가는 요청 => 다른 서버가 임시로 처리 (해시링에서 다음 서버)
-
임시 위탁(hinted handoff) 기법: 임시 처리 서버가 그 동안 발생한 변경 사항을 단서(hint)로 남겨두는 기법.
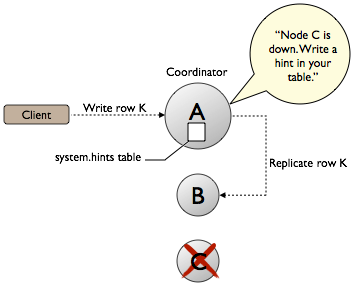
영구 장애 처리
앞에서 얘기한 단서 후 임시 위탁 기법은 "임시적" 장애를 처리하기 위함이다.
우리 노드의 장애가 영구적이 될 수 있는데, 이럴 때는 반-엔트로피 프로토콜을 구현해서 사본들을 동기화 할 것이다.
반-엔트로피(anti-entropy) 프로토콜
: 사본을 동기화하는 프로토콜 => 사본들을 비교하여 최신 버전으로 갱신하는 과정을 포함한다.
우리는 머클 트리를 사용해서 사본간 충돌을 탐지하고 전송 데이터의 양을 최소화한다.
머클트리
머클트리 (위키피디아)
해시트리라고도 불리는 머클트리는 각 노드에 그 자식 노드들에 보관된 값의 해시, 또는 자식 노드들의 레이블로부터 계산된 해시값을 테이블로 붙여두는 트리다. 해시 트리를 사용하면 대규모 자료 구조의 내용을 효과적이면서도 보안상 안전한 방법으로 검증할 수 있다.
책 108페이지
키 공간이 1부터 12까지일 때 머클 트리를 만드는 예제를 한번 살펴보자.
- 1단계: 키 공간을 4개의 버킷으로 나눔 (예제는 4개)
- 2단계: 버킷에 포함된 각각의 키에 균등 분포 해시 함수를 적용하여 해시 값을 계산한다
- 3단계: 버킷별로 해시값을 계산한 후, 해당 해시 값을 레이블로 갖는 노드를 만든다.
- 4단계: 자식 노드의 레이블로부터 새로운 해시값을 계산하여 이진트리를 상향식으로 구성해나간다.
완성
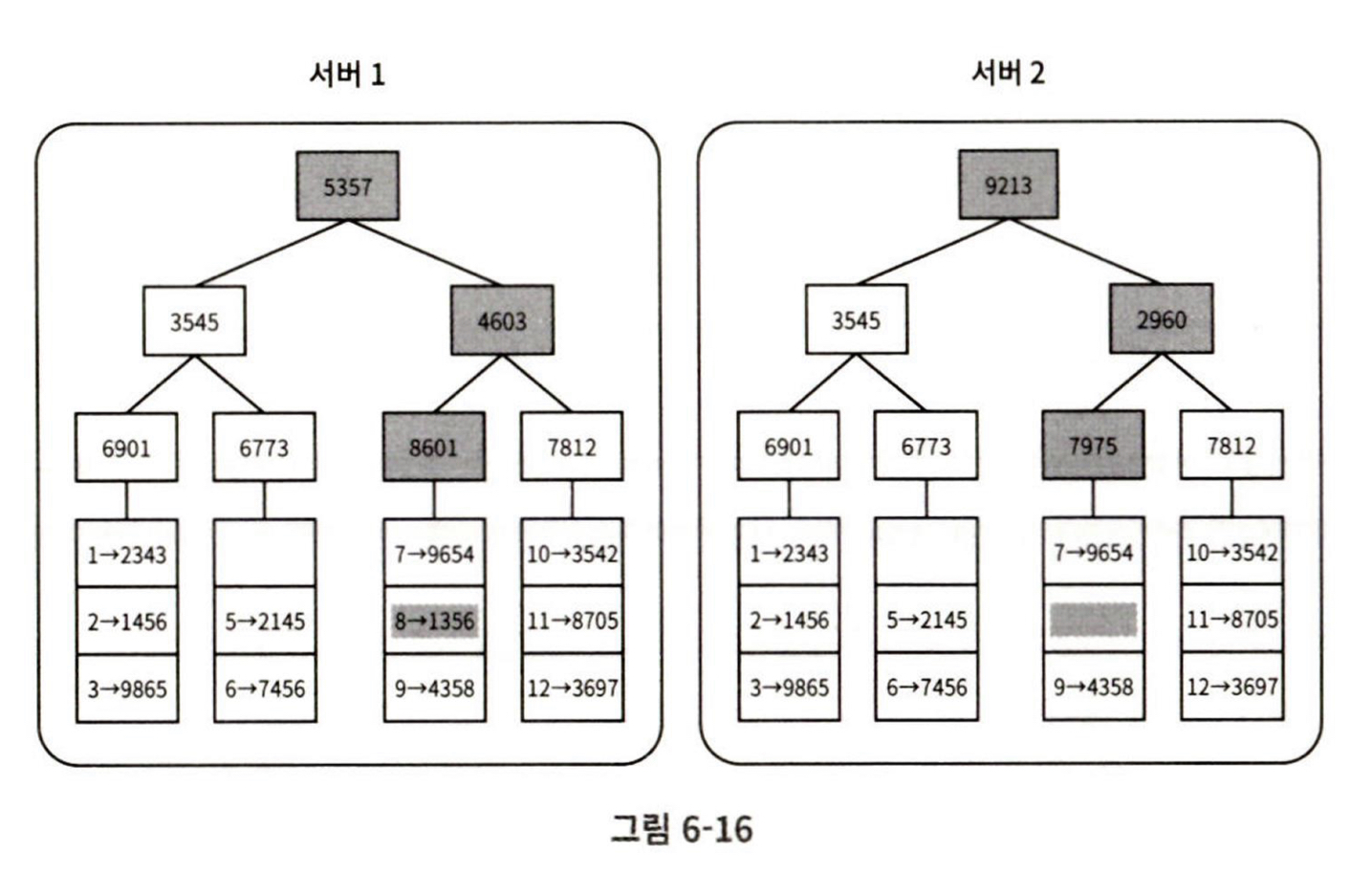
이 두 머클 트리의 비교는 루트 노드부터 시작하는 것이다. 루트 노드 같나면 나머지 자식의 해시값도 같다는 것으로 해석한다.
그렇지 않고 두 서버의 노드 값이 다르다면 자식노드 해시값들도 비교하는 것이다. 이렇게 하면서 아래쪽으로 탐색해나가면 다른 데이터를 갖는 버킷 (leaf)을 찾을 수 있어서 그 버킷들만 동기화하면 된다.
* 동기화 해야하는 데이터의 양은 실제로 존재하는 데이터 차이에 비례하게 된다 ~~
하지만 머클 트리의 버킷 하나의 크기도 꽤 크다. 10억개의 키를 백만개의 버킷으로 관리하는 경우 하나의 버킷은 1000개의 키를 관리하겠다.
데이터 센터 장애 처리
데이터 센터 장애는
- 정전
- 네트워크 장애
- 자연 재해
등 다양한 이유로 발생할 수 있다. 이런 문제에 대응하려면 여러 데이터 센터의 데이터 다중화가 중요해진다!!! (당연하다!!!)
시스템 아키텍처 다이어그램
- 클라이언트는 키-값 저장소가 제공하는 API
get(key)와put(key, value)로 통신한다. - 중재자는 클라이언트에게 키-값 저장소에 대한 프락시 역할을 하는 노드다.
- 노드는 안정해시의 해시링 위에 분포한다.
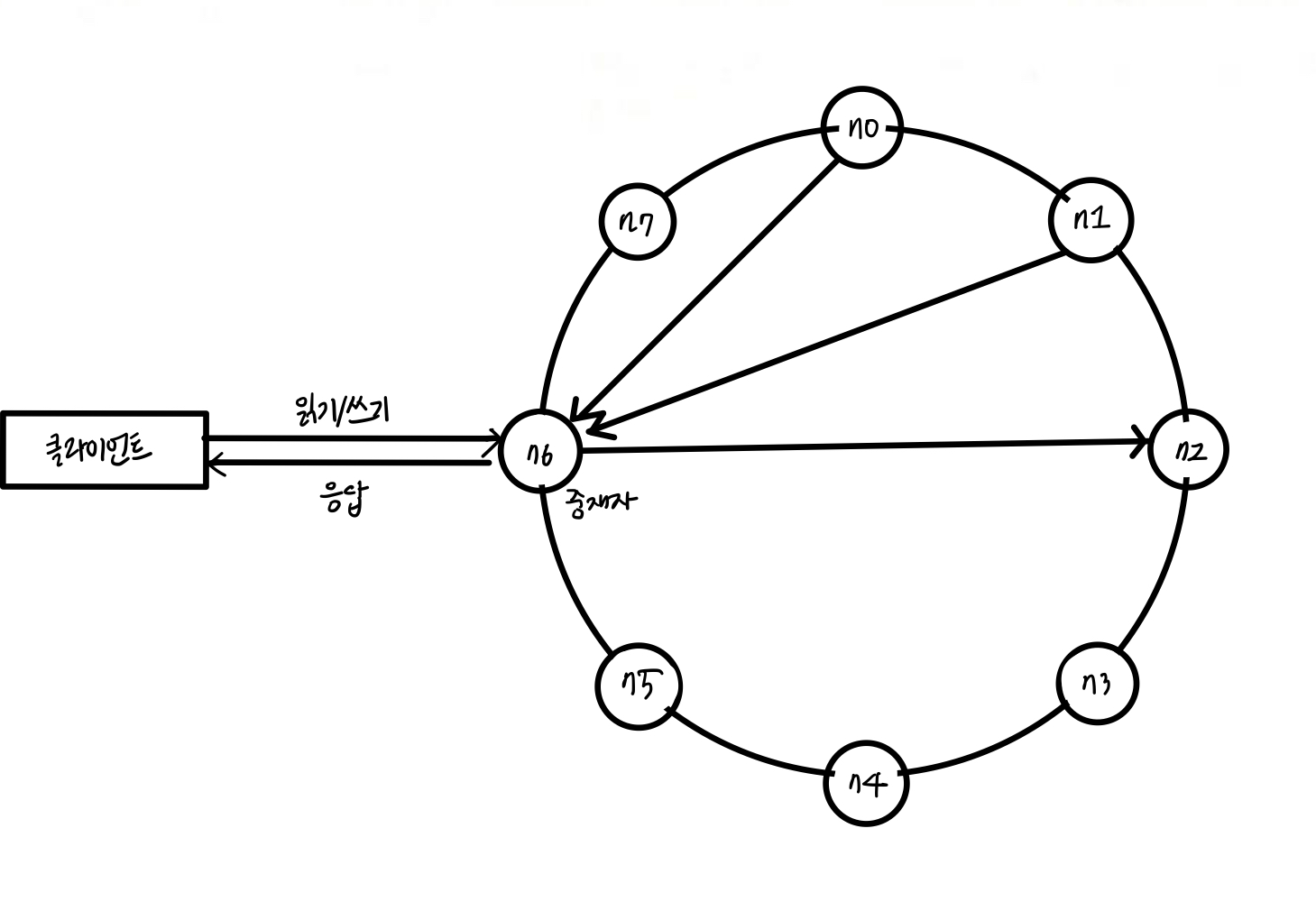
대충 따라그렸다..
쓰기 경로
- 쓰기 요청이 커밋 로그 파일에 기록된다.
- 데이터가 메모리 캐시에 기록된다.
- 메모리 캐시가 가득차거나 사전에 정의된 어떤 임계치에 도달하면 데이터는 디스크에 있는 SSTable에 기록된다. SSTable은 Sorted-String Table의 약어로, <키, 값>의 순서쌍을 정렬된 리스트 형태로 관리하는 테이블이다.
읽기 경로
읽기 요청을 받은 노드는 데이터가 메모리 캐시에 있는지부터 살핀다. 있는 경우에는 해당 데이터를 클라이언트에게 반환한다.
데이터가 메모리에 없는 경우에는 디스크에서 가져와야한다. 어느 SSTable에 키가 있는지 알아낼 방법으로 블룸 필터가 흔히 사용된다.
- 데이터가 메모리 있는지 검사한다. 없으면 2로 간다.
- 데이터가 메모리에 없으므로 블룸 필터를 검사한다.
- 블룸 필터를 통해 어떤 SSTable에 키가 보관되어 있는지 알아낸다.
- SSTable에서 데이터를 가져온다.
- 해당 데이터를 클라이언트에게 반환한다.