[백준] 1389번: 케빈베이컨의 6단계 법칙

문제보기

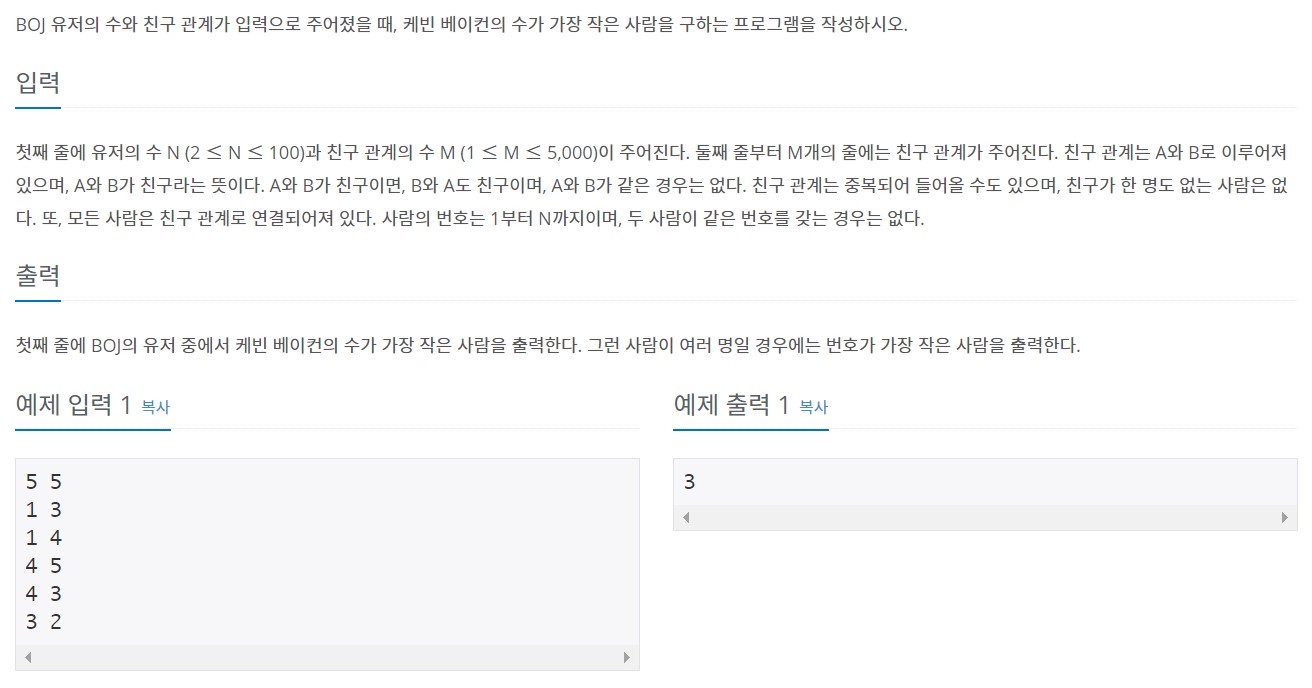
이 문제는 플로이드와샬 알고리즘을 사용하는 기본 문제다. 이전 문제 '플로이드'랑 거의 똑같다. 이 문제도 이 알고리즘만 몇 줄 쓰면 끝이다.

v, e = map(int, input().split())
s = [[6]*v for _ in range(v)]
for i in range(e):
    start, end = map(int, input().split())
    s[start-1][end-1] = s[end-1][start-1] = 1

for k in range(v):
    s[k][k] = 0
    for i in range(v):
        for j in range(v):
            if i != j:
                s[i][j] = min(s[i][j], s[i][k] + s[k][j])
minSum = 6*(v-1)
ans = 1
for i in range(v):
    if minSum > sum(s[i]):
        minSum = sum(s[i])
        ans = i+1
print(ans)

이번에는 최댓값에 유념하면서 풀었다..😂 이 문제에서는 모든 사람의 케빈베이컨의 수가 최대 6이라고 가정하므로 최단거리 배열을 6으로 초기화해주면 된다.

그리고 출력은 한 사람의 모든 케빈베이컨의 수의 합의 최솟값이니까, minsum을 케빈베이컨 수의 합의 최댓값으로 초기화해놓고 검사하면 된다.