[알고리즘] 분할정복🧨 히스토그램 풀이

분할정복 개념을 다시 보았다. 나는 이 글을 보고 공부했다.

Divide and Conquer

탐색, dp, 그리디 등에 비해서는 등장하는 빈도가 낮지만
이 기법의 성질 자체가 다른 여러 효율적인 자료구조나 알고리즘에 기여하는 경우가 많기 때문에 꼭 공부해야한다.

분할정복은 말 그대로 1. 분할 2. 정복 으로 나눠서 문제를 해결하는 것을 말한다.

주어진 문제를 여러 개의 부분 문제로 나누는 것이 분할 정복의 전략인데, 이 전략은 문제의 크기가 작아질수록 풀기 쉬워지는 성질을 이용한 것이다.

그니까, 분할정복은 이미 풀렸다고 볼 수 있는 작은 문제들을 합치는 데 필요한 연산이 적을 때 이용될 수 있다. -> 여러 답을 합쳐 하나의 답을 도출하는게 전체 문제 하나를 푸는 것보다 빠른 경우에 이용한다.

분할 정복은 재귀와 함께일 때가 많다!

기저 사례들로 각 문제의 답을 풀고, 이 작은 문제들을 호출했던 큰 문제는 이 답들로 자신의 답을 구할 수 있다.

대표적인 예시: 병합정렬(merge sort), 이분탐색, 거듭제곱 연산, 퀵정렬 등

분할정복 시간복잡도

분할정복 알고리즘의 수행시간을 얻기 위해서는

1. 나누어지는 문제의 개수
2. 분할 후 문제의 크기
3. 각 문제마다 병합 단계에서 걸리는 시간

을 파악해야 한다.

각 단계에서 [병합하는 횟수]*[해당 단계의 문제의 크기] 가 수행시간이 된다.

문제의 총 수행시간은 단계마다의 수행시간을 더해주면 되는 거겠지.

예를 들어, 병합정렬의 경우

1. 나누어지는 문제의 개수: 2
2. 분할 후 문제의 크기: N/2
   => 병합 횟수: k단계에서 2^k번
3. 병합 단계에서 걸리는 시간복잡도: O(N)

따라서 0 <= k < log₂N + 1 단계의 시간복잡도는
2^k * O(N/2^k) = O(N)이다

그래서 전체 시간복잡도는 병합횟수(log₂N) 을 곱한
O(NlogN)이 된다.

---

분할정복의 대표 문제라고 하는 히스토그램👈🏻을 파이썬으로 다시 풀이했다.

주어진 히스토그램 안에서 그릴 수 있는 가장 큰 직사각형의 넓이를 구하는 문제였다.

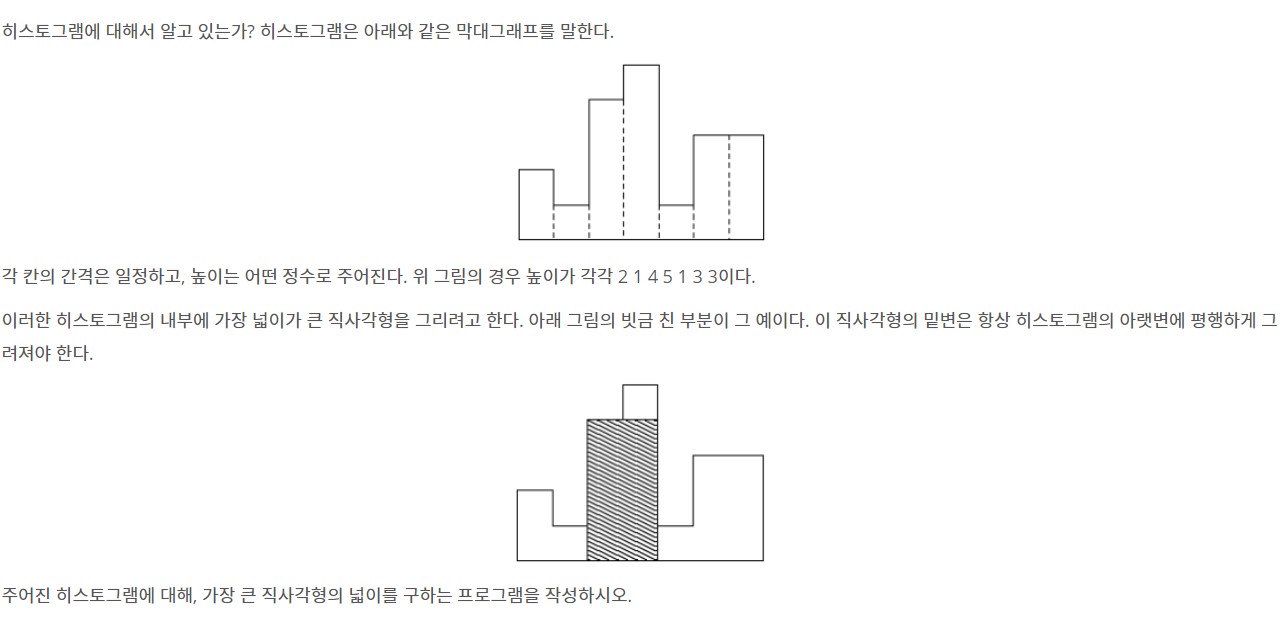
분할 정복 문제라는 걸 이미 알고 있는 상태였는데도 이 문제를 어떤 작은 문제로 분할하는지 잘 떠오르지 않았다.

그래서 설명을 보면서 먼저 이해부터 해보려고 했다. 우선 이 문제는 큰 문제를 다음의 세 가지 부분문제로 나누어야 한다.

히스토그램의 가로를 인덱스로 번호를 붙였을 때, 중앙값(mid)를 중심으로

1. 왼쪽에서의 최대 직사각형 넓이
2. 오른쪽에서의 최대 직사각형 넓이
3. 🎈 왼,오 모두 걸치는 최대 직사각형 넓이 🎈

를 구해서 이 세 개의 부분문제의 답 중에 가장 큰 값으로 고르는 것이었다.

코드를 보면, solve 함수에서 1번과 2번의 경우는 재귀호출로 구했고, 3번은 반복문으로 구한다. 1과 2는 그 안에서 또 세개로 쪼개지고 쪼개지고.. 기저까지 내려가서 알아서 최대 넓이가 구해지는 것이다.

mid = (s + e) // 2
# 1번과 2번 구하고 둘 중에 최댓값 저장
result = max(solve(s, mid), solve(mid, e))

3번의 경우가 직접 구현해야하는 부분이었다. 가운데에서부터 가로의 길이를 1로 하고 시작해야한다.

while r-l+1 < e-s: #색칠한 부분의 가로 길이가 e-s 보다 작으면 반복
    p = min(h, arr[l-1]) if l > s else -1 #l의 범위가 올바르면
    q = min(h, arr[r+1]) if r < e-1 else -1 #r의 범위가 올바르면

    if p >= q:
        h = p
        l -= 1
    else:
        h = q
        r += 1
    w += 1
    result = max(result, w*h)

반복하는 각 단계에서, 왼쪽/오른쪽 중 더 긴 쪽을 선택하고 선택한 히스토그램을 하나의 부분문제로 볼 수 있는 것이다.

계속해서 높이 최솟값인 h를 갱신하면서 넓이를 계산해보고 기존의 result보다 큰 값이 나오면 result에 저장하면 된다.

정답 전체

N = int(input())
arr = []
for _ in range(N):
    arr.append(int(input()))

# 분할정복으로 [s, e) 문제를 푸는 함수
def solve(s, e):
    if s == e:
        return 0
    if s+1 == e:
        return arr[s]

    mid = (s + e) // 2
    result = max(solve(s, mid), solve(mid, e))

    w = 1
    h = arr[mid]
    l = mid
    r = mid

    while r-l+1 < e-s:
        p = min(h, arr[l-1]) if l > s else -1
        q = min(h, arr[r+1]) if r < e-1 else -1
        
        if p >= q:
            h = p
            l -= 1
        else:
            h = q
            r += 1
        w += 1
        result = max(result, w*h)

    return result


print(solve(0, N))

---

쉽지 않다 ^^..