[자료구조] AVL 트리

저번학기에 공부할 때부터 많이 헷갈렸었던 AVL트리다.

AVL트리란?

트리 T의 모든 내부노드 v에 대해 자식들의 좌우 높이 차가 1이 넘지 않는 이진탐색트리이다.

• AVL 트리의 부트리 역시 AVL트리
• 높이 정보는 각 내부노드에 저장

n개의 항목을 저장하는 AVL트리의 높이는 O(logn)이다.

자꾸 까먹는데, AVL트리를 이진탐색트리와 분리하려하지 말자. AVL의 restructuring을 이해하려면 AVL이 이진탐색트리인것을 잊으면 안 된다.

AVL트리 Insertion/Deletion (갱신)

: 갱신 이후에 높이 균형 속성이 파괴될 수 있으므로 balance check 후 restructuring 진행.

갱신 이후 restructure

Alg searchAndFixAfterInsertion(w)
  // x, y, z 노드 정하기 :)
  1. w에서 T의 루트로 향해 올라가다 처음 만나는 불균형 노드를 z라 하자.
  2. z의 높은 자식을 y라 하자. {나중에 y가 w의 조상이 된다.}
  3. y의 높은 자식을 x라 하자
  4. restructure(x, y, z)
  5. return

Restructure(x, y, z)

: 회전이라고 불리기도 한다.

이해해보기.

1. x, y, z 의 중위 순회 순서를 a, b, c라고 하자 (그냥 오름차순임)
2. 결과를 먼저 말하자면, b가 부모가 되고 a, c가 자식이 될 것이다. 어찌보면 당연한 소리지만 이걸 생각하면서 알고리즘을 생각하면 좀 더 빨리 이해할 수 있다.

    z           z           z            z
   /           /             \            \
  y           y               y            y
 /             \               \          /
x               x               x        x 

이렇게 네 경우가 있다. 타이핑 너무 귀찮으니까 이제 그림으로 그려야겠다.

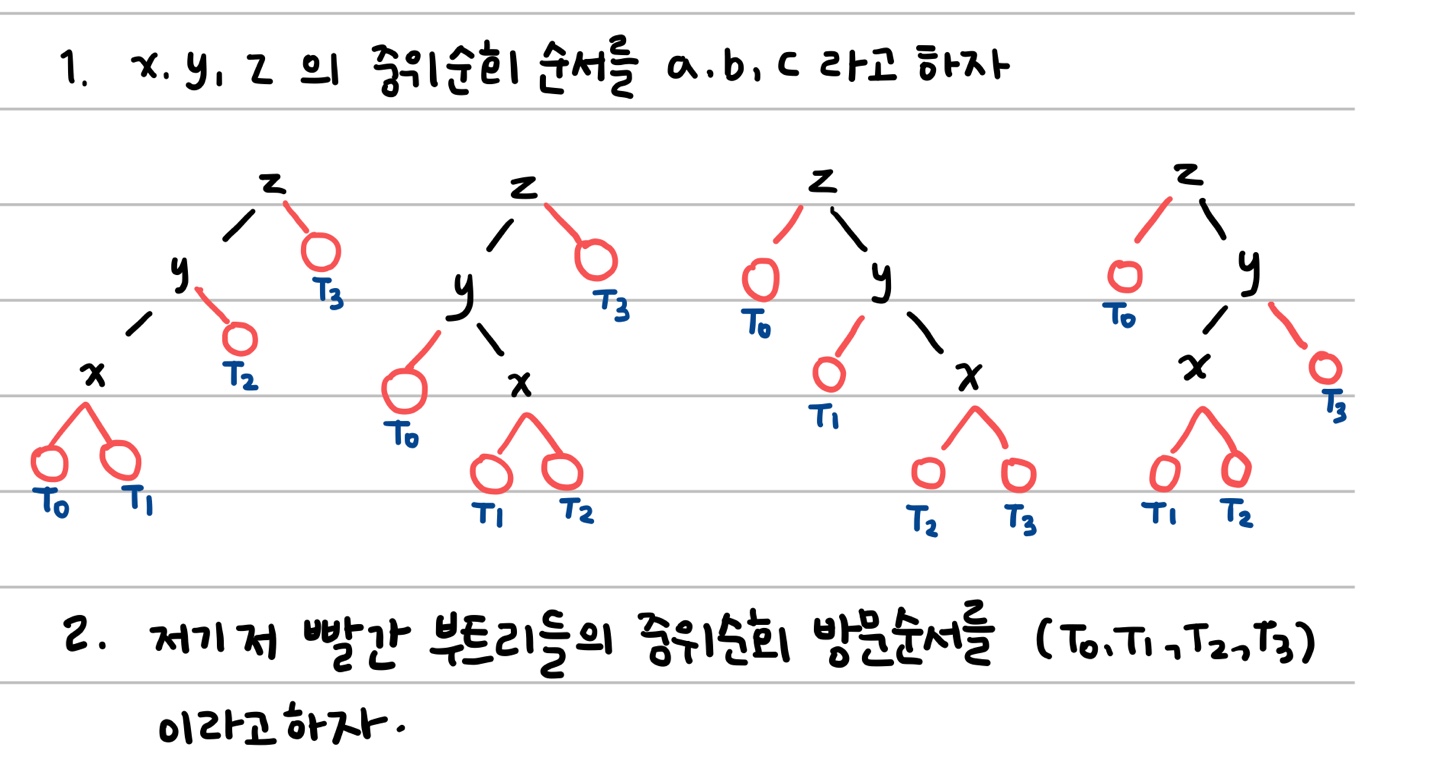
중위순회 순서는 오름차순이라는 뜻. 그냥 법이다 법 잊지 말자

개조 시작 ~ 👻
1. z를 루트로 하는 부트리(빨간 거 말고 y랑 연결돼있는 부분)를 b를 루트로 하는 부트리로 대체.
👉🏻 이렇게 하면 가운데에 오는 애가 z 자리로 가는 거 알겠지?

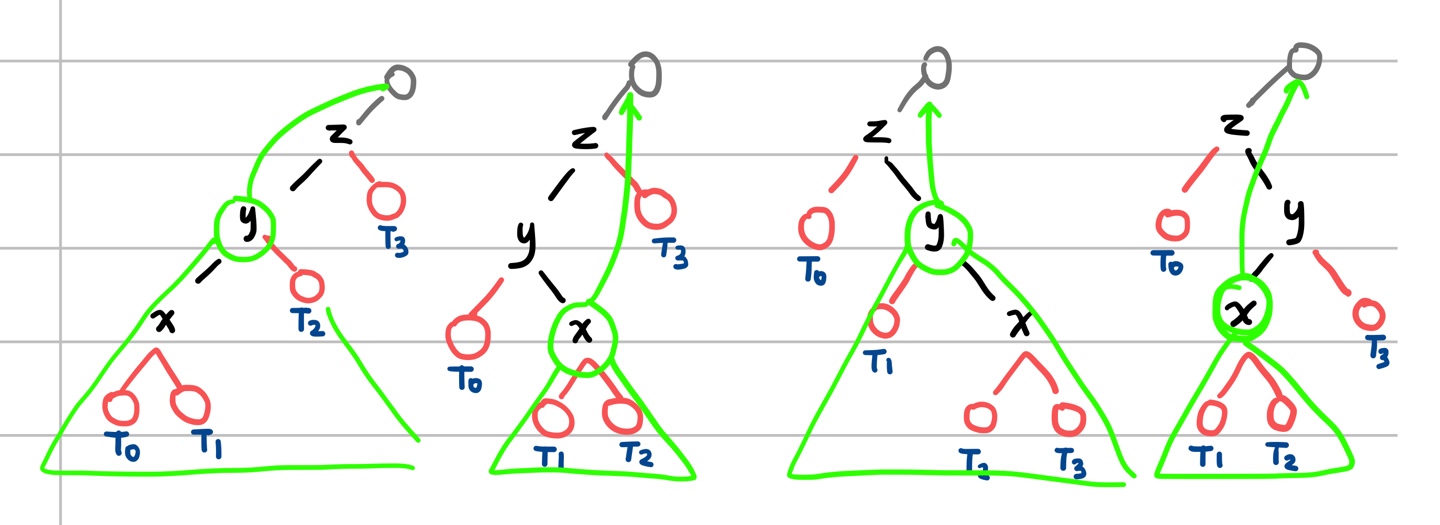
그 다음엔 아까 찾았었던 빨간 부트리들을 a와 c에 붙여준다.
2. T_0와 T_1을 a의 왼쪽, 오른쪽 부트리로 만든다.
3. T_2와 T_3을 c의 왼쪽, 오른쪽 부트리로 만든다.

코드로 구현하면 다음과 같다. 음.. 한 세 번째 보는 거지만 볼 때마다 헷갈려서 적어봤다.

이걸 다시 볼 일이 있을진 모르겠다.

TreeNode* restructure(TreeType* T, TreeNode* x) {
  TreeNode* y, * z, * a, * b, * c; // 부모, 부모의 부모
  TreeNode* T0, * T1, * T2, * T3;
  
  y = x->parent; printf("y = x->parent 대입\n");
  printf("y: %d\n", y->key);
  printf("z: %d\n", y->parent->key);
  
  printf("x = y->parent 대입\n");
  z = y->parent;
  if (z->key < y->key && y->key < x->key) { // z < y < x
    a = z;
    b = y;
    c = x;
    T0 = a->left;
    T1 = b->left;
    T2 = c->left;
    T3 = c->right;
  } else if (z->key > y->key && y->key > x->key) { // x < y < z
    a = x;
    b = y;
    c = z;
    T0 = a->left;
    T1 = a->right;
    T2 = b->right;
    T3 = c->right;
  } else if (z->key < x->key && x->key < y->key) { // z < x < y
    a = z;
    b = x;
    c = y;
    T0 = a->left;
    T1 = b->left;
    T2 = b->right;
    T3 = c->right;
  } else { // y < x < z
    a = y;
    b = x;
    c = z;
    T0 = a->left;
    T1 = b->left;
    T2 = b->right;
    T3 = c->right;
  }

  //3.
  if(z == T->root) {
    T->root = b;
    b->parent = NULL;
  } else if (z->parent->left == z) {
    z->parent->left = b;
    b->parent = z->parent;
  } else {
    z->parent->right = b;
    b->parent = z->parent;
  }
  // 4.
  a->left = T0;
  T0->parent = a;
  a->right = T1;
  T1->parent = a;
  a->height = max(T0->height, T1->height) + 1;

  // 5.
  c->left = T2;
  T2->parent = c;
  c->right = T3;
  T3->parent = c;
  c->height = max(T2->height, T3->height) + 1;

  // 6.
  b->left = a;
  a->parent = b;
  b->right = c;
  c->parent = b;
  b->height = max(a->height, c->height) + 1;

  return b;
}