백준 1644번

백준 1644번

한 숫자가 주어졌을 때 그 소수를 하나 이상의 연속된 소수의 합으로 나타낼 수 있는지, 나타낼 수 있으면 몇가지 경우의 수가 있는지 출력하는 문제이다.

해당 문제는 에라토스테네스의 체와 이중포인터를 사용하여 해결하는 문제이다. 우선 에라토스테네스의 체로 소수의 배열을 만든 뒤 그 배열에서 이중포인터를 사용하여 그 포인터들의 사이에 있는 소수들의 합이 n이 되는 경우가 있는지, 있다면 그 cnt를 1씩 추가하여 계속 해서 진행하면 된다.

에라토스테네스의 체

100은 소수일까? 100의 약수를 구하기 위해 곱셈으로 100을 만들어보자. 1100, 250, 425, 1010, 20 5, 254, 1001. 이때 1, 2, 4, 10, 25, 50, 100이 100의 약수이다. 따라서 100은 소수가 아니다. 근데 굳이 100의 약수를 100까지 확인할 필요가 있을까? 사실 100의 제곱근 즉 10까지만 점검해도 충분하다. 생각해보면 어차피 425, 25*4는 똑같은 숫자들이기 때문이다. 소수를 판별하려는 수의 제곱근까지만 수를 나눌 수 있는지 판별하는 것만으로 충분하다는 것이다. 이 방식으로 특정한 수가 소수인지 아닌지는 쉽게 판별할 수 있다.

그러면 어떤 수까지의 소수의 목록을 쫙 뽑을 수는 없을까? 에라토스테네스의 체로 구현할 수 있다. 에라토스테네스는 특정한 수까지의 모든 소수들을 구할 수 있는 방식을 고안하였다. 마치 체를 이용하여 거르는 방식같아서 에라토스테네스의 체라고한다. 방식은 아래와 같다.

1. 2부터 시작하여 본인을 제외한 자신의 배수를 모두 제거해준다.
2. 제거된 수에서는 해당 로직을 수행하지 않는다.

예를 들어 10까지 에라토스테네스의 체를 이용하여 소수를 구해보겠다.

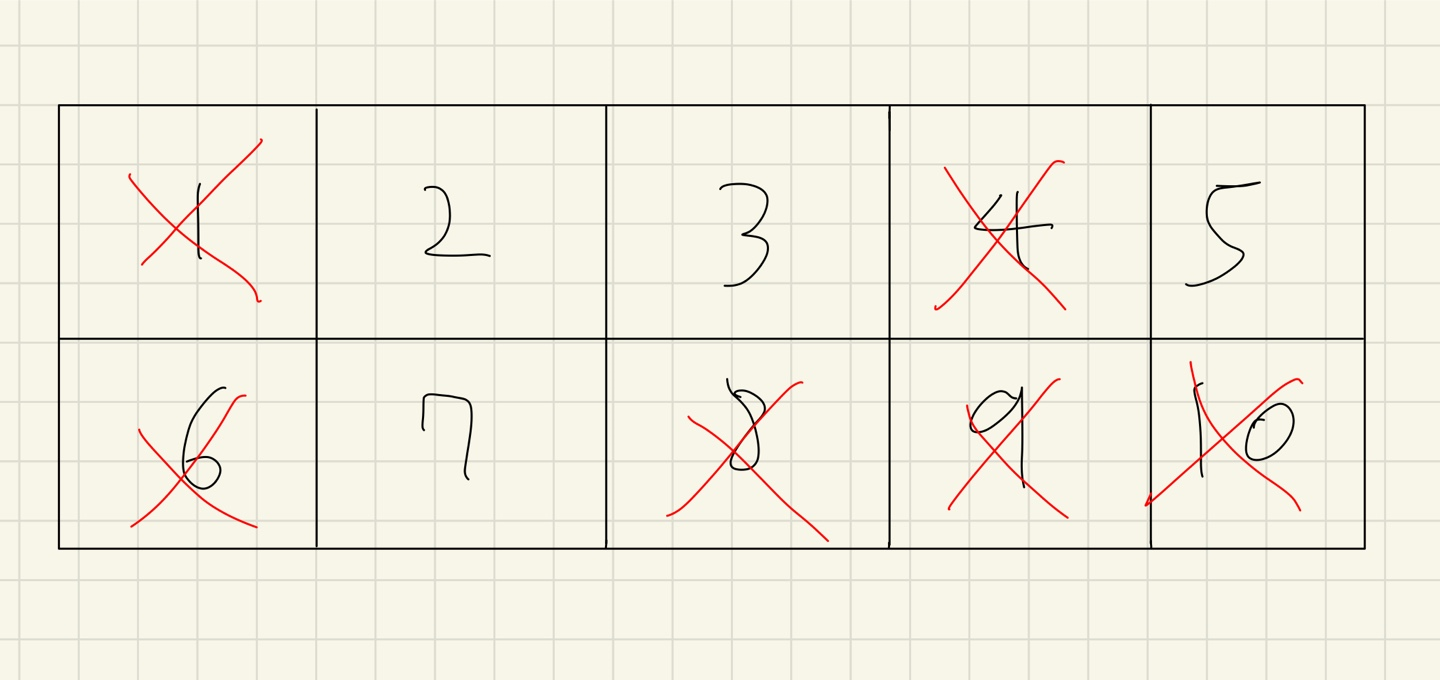
문제 풀이 코드

#include <bits/stdc++.h>

using namespace std;

const int  MAX = 4000000;
int arr[MAX + 1];

int main() {
	int n;
	scanf_s("%d", &n);
	
	if (n == 1) {
		printf("0");
		return 0;
	}

	for (int i = 2; i <= n; i++) {
		arr[i] = i;
	}

	// 에라토스테네스의 체
	for (int i = 2; i <= MAX; i++) {
		for (int j = i + i; j <= MAX; j += i) {
			arr[j] = 0;
		}
	}
	vector<int> v;
	for (int i = 2; i <= n; i++) {
		if (!arr[i])
			continue;
		v.push_back(arr[i]);
	}

	int l = 0;
	int r = 0;
	int sum = v[0];
	int cnt = 0;
	while (l <= r && l < v.size() && r < v.size()) {
		if (sum < n) {
			r++;
			if (r == v.size()) {
				break;
			}
			sum += v[r];
		}
		else if (sum == n) {
			cnt++;
			sum -= v[l];
			l++;
		}
		else {
			sum -= v[l];
			l++;
		}
	}

	printf("%d", cnt);
}