백준 1865번

백준 1865번 (웜홀)

해당 문제는 처음에 읽었을 때 어찌 풀어야할지 감이 오지 않았다. 그라다가 플로이드와샬 알고리즘을 이용해서 풀 수 있을 것 같았다. 하지만 바로 오답을 맞아버렸다.

생각해보니 시간을 돌릴 수 있어서 음수의 간선이 있다는 것을 간과하였다. 음수의 간선이 있기에 벨만포드를 사용해야하는 문제였다. 또한 그 안에서 음수 싸이클을 찾아야해결 되는 문제였다.

하지만 벨만포드를 사용해도 문제가 해결되지않았다. 내가 너무 멍청하게도 입력을 잘못받고 있었다. 근데 또 고치고 제출하니 오답을 맞았다. 🤔 너무 화가 났지만 생각해보니 오류가 날 수 밖에 없었다. 기존의 벨만포드는 한 시작점에서 다른 정점들까지의 최소 거리를 구해준다. 근데 그렇다보니 해당 정점과 구분되어 있는 반례가 있었다.

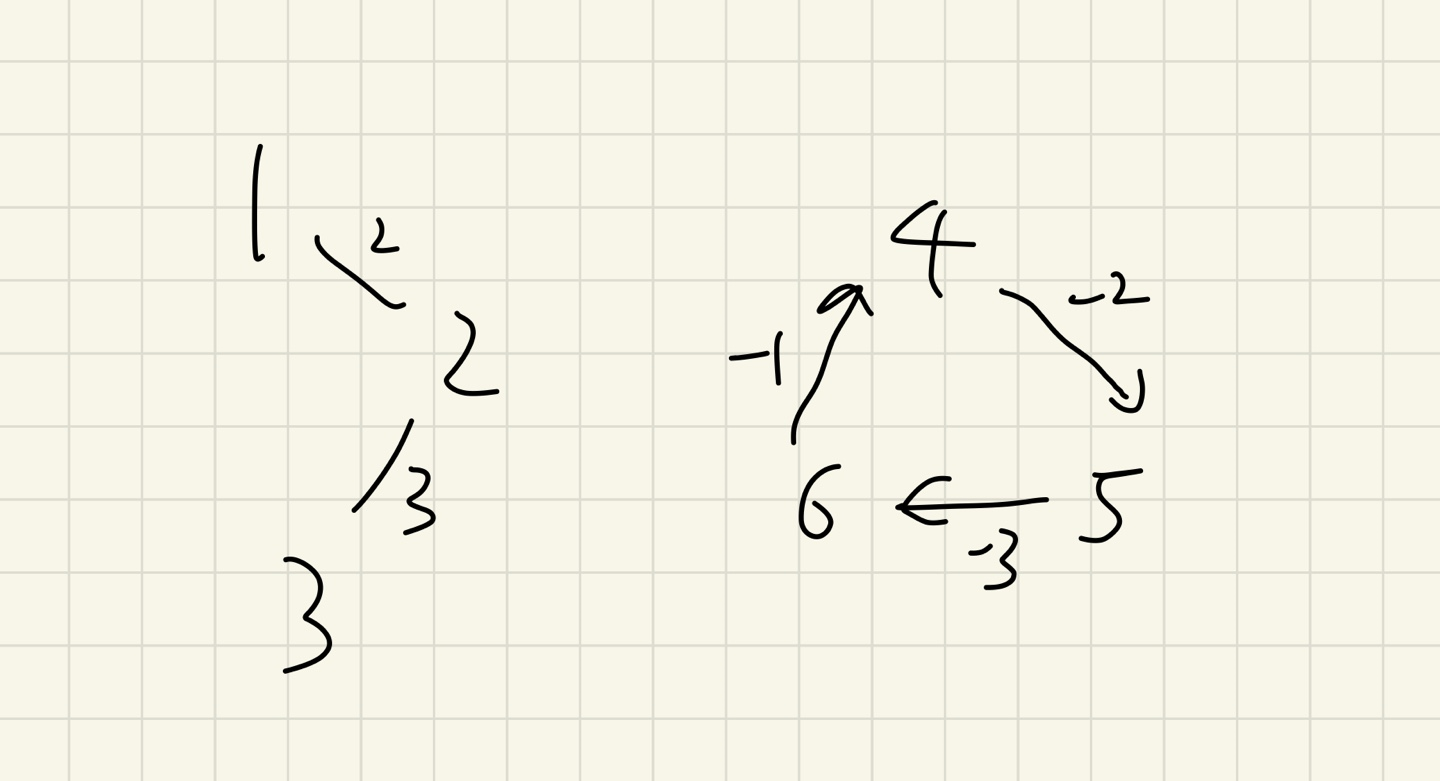
이 경우 한 정점에서만 벨만포드를 돌리면 정답을 얻을 수 없다. 그렇기에 모든 정점에 대해서 수행해주었다. 이건 결과를 알고 있었다. 시간초과를 받았다. 당연히 애초에 시간복잡도가 있는 알고리즘인데 그것을 모든 정점에 수행하니 시간초과가 날 것이라 예상하였다.

결국 시작점이 매우 큰 수 INF인지 점검하는 로직을 제거하여 해결할 수 있었다. 원래 INF는 해당 정점과 분리되어 있다는 것을 명시하기위해 사용하였다. 그로인해 시작 정점을 0으로 시작하여 시작 정점과 연결된 정점들만, 그 안에서 최단거리를 구한 것이다. 하지만 해당 문제는 음수 싸이클의 존재 여부만 알면 되기에 해당 INF비교를 제거하면 한 번의 벨만포드만 돌려도 해결할 수 있었다.

#include <bits/stdc++.h>

using namespace std;


struct EDGE {
	int from, to, w;
};

vector<EDGE> edges;

vector<int> BellmanFord(int v) {
    vector<int> res(v + 1);
    for (int i = 1; i <= v; ++i) {
        for (int j = 0; j < edges.size(); ++j) {
            int s = edges[j].from, t = edges[j].to, w = edges[j].w;
            if (res[t] > res[s] + w) {
                if (i == v) {
                    res[0] = -1;
                    return res;
                }
                res[t] = res[s] + w;
            }
        }
    }
    return res;
}

int main() {
	int tc;
	scanf_s("%d", &tc);

    for (int i = 0; i < tc; i++) {
        int n, m, w;
        bool flag = false;
        scanf_s("%d %d %d", &n, &m, &w);

        int s, e, t;
        for (int j = 0; j < m; j++) {
            scanf_s("%d %d %d", &s, &e, &t);
            edges.push_back({ s, e, t });
            edges.push_back({ e, s, t });
        }
        for (int j = 0; j < w; j++) {
            scanf_s("%d %d %d", &s, &e, &t);
            edges.push_back({ s, e, -t });
        }
        vector<int> result = BellmanFord(n);
        if (result[0] == -1) {
            printf("YES\n");
        }
        else {
            printf("NO\n");
        }

        edges.clear();
    }
	return 0;
}