Laplacian Filter는 [[엣지 검출]]에 이용되는 필터 중 하나이다.
경계를 검출하는데 미분이 사용되는데,
1차미분
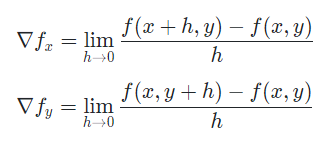
1차 미분은 함수의 기울기를 알 수 있다.
픽셀에서 대해서 h가 0으로 수렴이 안되고 최대한 수렴한다했을 때 인접 픽셀인 바로 옆 픽셀과의 거리인 h=1 이 될 수 있다.
2차미분
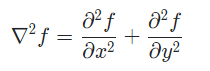
2차 미분은 함수의 곡률을 알아낼 수 있다.
라플라시안 필터는 이미지의 밝기 값의 변화율이 큰 지점을 감지하기 위해 2차 미분을 사용한다.
어떻게보면 노이즈가 크게 튀는 부분을 찾아내기 때문에 [[Highpass]]와 유사한 결과를 보인다.
예를들어 3 x 3 사이즈를 살펴보면 다음과 같다.
int filter3[3][3] = {
{-1, -1, -1},
{-1, 8, -1},
{-1, -1, -1}이런 형태로 각 인덱스들의 합이 0이 되게 유지하면서 중앙에 위치한 인덱스의 frequency가 튀도록 한다.
이제 배열에서 현재 픽셀 위치에 해당하는 값을 가져와, 필터 마스크의 해당 위치의 가중치와 곱한 후 sum 변수에 누적한다.
void CImageDlg::LaplacianFilter()
{
// 이미지가 로드되지 않았으면 반환
if (m_original == nullptr)
return;
// 결과를 저장할 임시 이미지 생성
BYTE* temp = new BYTE[IMAGE_SIZE];
memcpy(temp, m_original, IMAGE_SIZE);
// 필터 크기 설정
int pad = filterSize / 2;
// 라플라시안 필터 정의
int filter3[3][3] = {
{-1, -1, -1},
{-1, 8, -1},
{-1, -1, -1}
}; //중앙 픽셀의 가중치가 높게 설정됨. (3x3)
int filter5[5][5] = {
{-1, -1, -1, -1, -1},
{-1, -1, -1, -1, -1},
{-1, -1, 24, -1, -1},
{-1, -1, -1, -1, -1},
{-1, -1, -1, -1, -1}
}; // (5x5)
// 각 픽셀에 대해
for (int y = pad; y < IMAGE_HEIGHT - pad; y++) {
for (int x = pad; x < IMAGE_WIDTH - pad; x++) {
int sum = 0;
// 필터 적용
for (int i = -pad; i <= pad; i++) {
for (int j = -pad; j <= pad; j++) {
if (filterSize == 3)
sum += m_original[(y + i) * IMAGE_WIDTH + (x + j)] * filter3[i + pad][j + pad];
else if (filterSize == 5)
sum += m_original[(y + i) * IMAGE_WIDTH + (x + j)] * filter5[i + pad][j + pad];
}
}
// 필터 적용 결과가 0보다 작으면 0, 255보다 크면 255로 설정
if (sum < 0) sum = 0;
if (sum > 255) sum = 255;
// 결과를 임시 이미지에 저장
temp[y * IMAGE_WIDTH + x] = sum;
}
}
// 결과를 m_filtered에 복사
memcpy(m_filtered, temp, IMAGE_SIZE);
delete[] temp; // 할당 해제
}그러나 라플라시안 필터는 높은 주파수의 노이즈가 출현한다면 미분값의 기울기가 급격히 증가해서 노이즈에 지나치게 민감하게 반응할 수 있다. 그래서 노이즈를 줄이기 위해 [[Gaussian Filter]]를 사용하기도 한다.
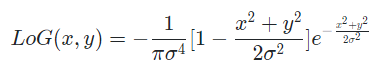
가우시안 필터를 반영하면 다음과같이 가중치를 할당할 수 있겠다.
[ 0, 0,-1, 0, 0],
[ 0,-1,-2,-1, 0],
[-1,-2,16,-2,-1],
[ 0,-1,-2,-1, 0],
[ 0, 0,-1, 0, 0]장단점
라플라시안 필터는 이미지의 경계선이나 에지를 감지하는 데 사용되는 필터로, 이미지에서 높은 주파수 구성 요소를 강조하는 특징이 있다. 장점으로는 세밀한 부분이나 경계선을 뚜렷하게 만들 수 있다는 점이 있다. 하지만 단점으로는 이미지 내의 노이즈도 함께 강조할 수 있다는 점이있다.
