벡터 : 크기와 방향을 동시에 나타내는 물리량
벡터는 보통 수학 좌표계를 통해서 나타낸다.
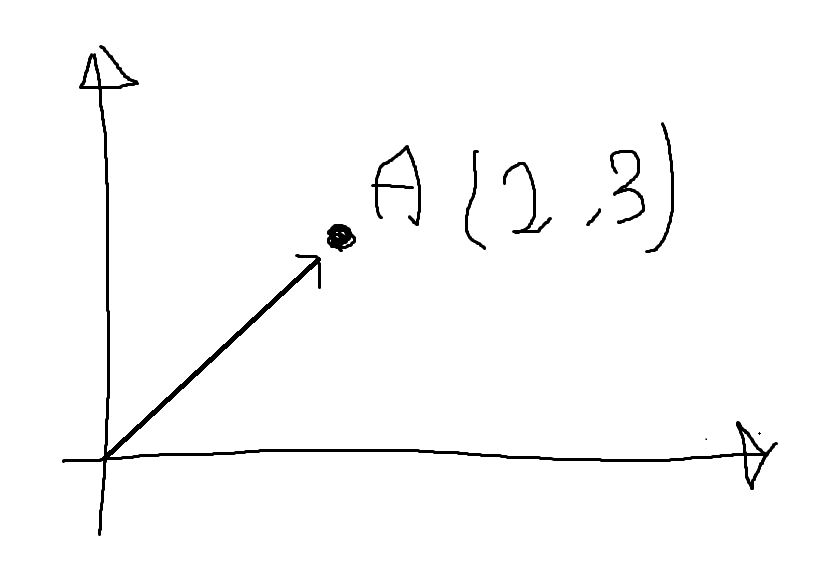
여기서 A점이 벡터이다.
스칼라는 벡터의 크기량을 의미하며 피타고라스 정리를 통해서 값을 얻어낼 수 있다.
__
이 경우 벡터 A의 스칼라는 |/13 이다.
벡터와 벡터 사이의 벡터
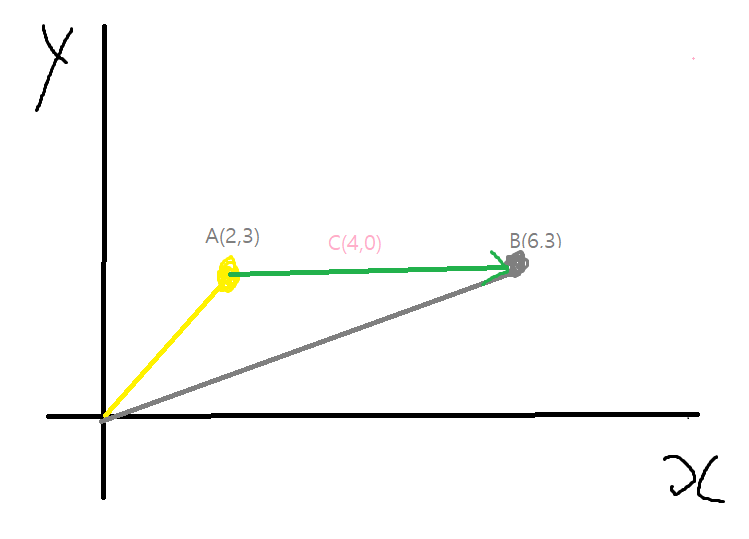
벡터 A에서 B로가는 벡터 C를 구하는 방법은 간단하게
C = B - A 로 구할 수 있다.
단순하게 벡터 B를 A가 이동한 위치만큼 원점을 조정한다고 생각하면 이해하기 쉽다.
단위 벡터 (유닛벡터)
단위 벡터는 벡터의 스칼라가 1인 벡터이다.
주로 방향을 나타내는 벡터를 표시할때 사용하는 벡터이다. ( 자주 쓰인다. )
A = 벡터
a = 벡터 A 의 x값
b = 벡터 A 의 y값
S = 벡터의 스칼라값
U = 유닛벡터
U = (a/S, b/S)
내적 (Dot Product)
벡터끼리 내적한 값은 스칼라가 나온다.
A = (1,2)
B = (3,4)
A * B = 1*3 + 2*4 = 11
벡터의 내적은 기하학적으로 큰 의미를 가지고 있다.
단위 벡터로 내적
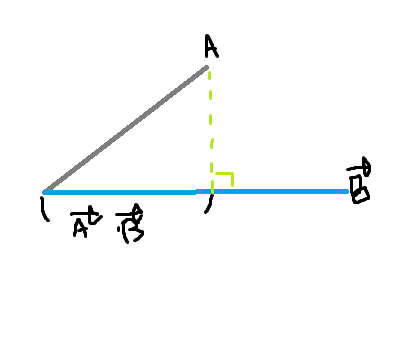
만약 벡터 B가 단위 벡터이고
A * B 연산을 수행한다면 결과값은 A 벡터를 B 벡터로 투영한 값과 동일하다.
A * B = |A| * |B| * cos(theta) 이고 B 벡터가 단위 벡터이기때문에
A * B = |A| * cos (theta) 삼각함수로 정리하면 A * B 는 B에 투영한 값이 나온다.
중요한것은 theta값이 변화함에 따라 A * B 값도 변화한다.
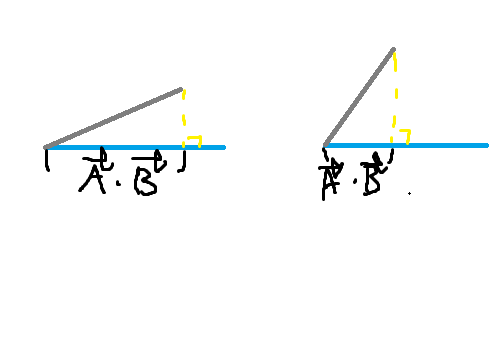
theta의 값이 줄어들면 A * B 값은 증가하고
theta의 값이 늘어나면 A * B 값은 감소하는 기하학적 의미를 가지고 있다.
위 의미를 다른 시각으로 바라보면 아래처럼 해석할 수 있다.
A*B 값이 작다면 서로 같은 방향을 바라보고 있다.
A*B 값이 크다면 서로 다른 방향을 바라보고 있다.
외적 (Cross Product)
외적은 3차원을 표현할때 자주 사용한다.
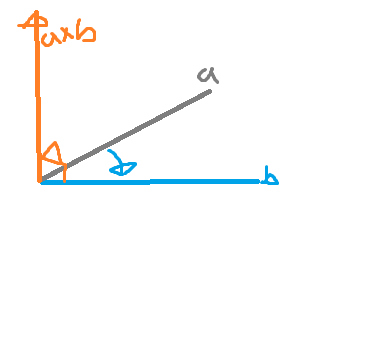
A X B 벡터는 3차원 벡터가 나온다.
A X B 벡터는 연산 A와 B의 수직인 벡터이기 때문에
A*(AXB) = 0
B*(AXB) = 0
값이 나온다.
또한 내적과 다르게 "벡터" 가 나온다는것도 주의할 점이다.
AXB 벡터의 방향은 어떤 좌표계를 가지고 있느냐에 따라 다른 방향이 나온다. 위에선 왼손 좌표계로
왼손으로 A -> B를 감싸고 엄지손가락이 가리키는 방향이 AXB 벡터의 방향이다.
오른손 좌표계는 또 다른 방향이 나온다는것도 유의해야한다.
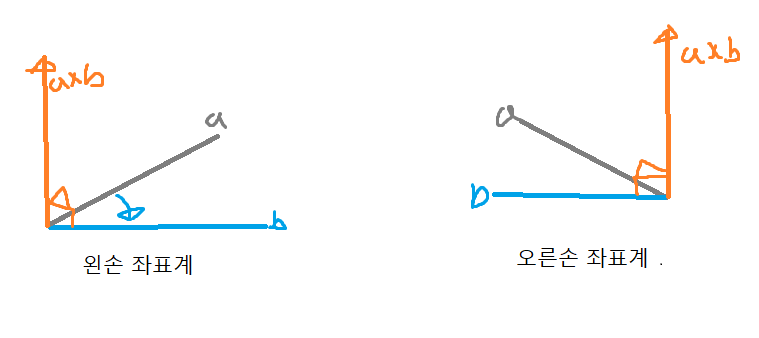
DirectX는 왼손 좌표계를 사용한다.

AXB의 크기는 a벡터 b 벡터로 만든 삼각형 "넓이" 의 2배이다.