[BJ / 17087] 숨바꼭질6

문제

수빈이는 동생 N명과 숨바꼭질을 하고 있다. 수빈이는 현재 점 S에 있고, 동생은 A1, A2, ..., AN에 있다.

수빈이는 걸어서 이동을 할 수 있다. 수빈이의 위치가 X일때 걷는다면 1초 후에 X+D나 X-D로 이동할 수 있다. 수빈이의 위치가 동생이 있는 위치와 같으면, 동생을 찾았다고 한다.

모든 동생을 찾기위해 D의 값을 정하려고 한다. 가능한 D의 최댓값을 구해보자.

입력

첫째 줄에 N(1 ≤ N ≤ 105)과 S(1 ≤ S ≤ 109)가 주어진다. 둘째 줄에 동생의 위치 Ai(1 ≤ Ai ≤ 109)가 주어진다. 동생의 위치는 모두 다르며, 수빈이의 위치와 같지 않다.

출력

가능한 D값의 최댓값을 출력한다.

예시

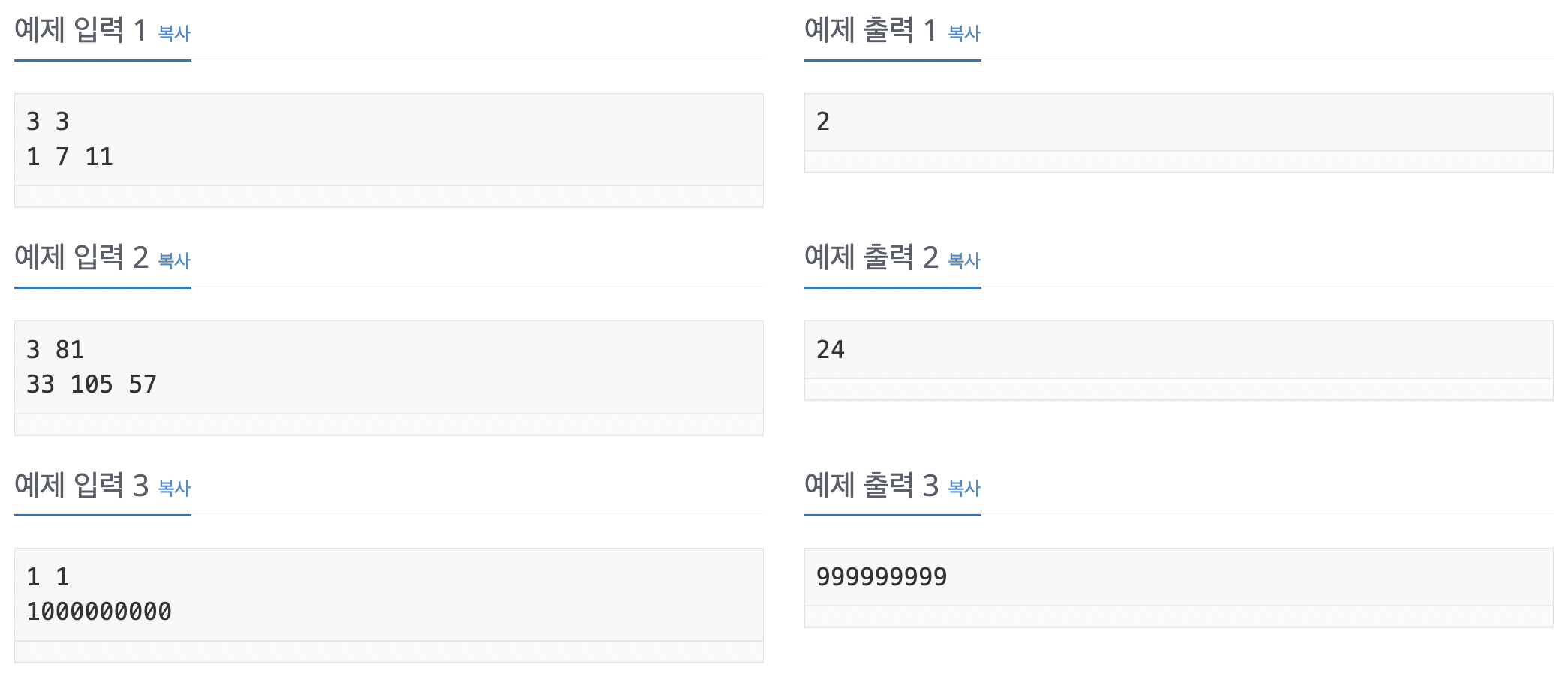
풀이

수빈이와 각 동생 간의 거리를 구한 다음, 그 거리들의 최대공약수를 구하는 방식으로 구현했다.

const readline = require('readline');

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

let input = [];
rl.on('line', (line) => {
  input.push(line);
});

rl.on('close', () => {
  let array = input[1].split(' ').map((el) => parseInt(el));
  console.log(solution(input[0].split(' ')[1], array));
});

function solution(loca, younger) {
  let gcd = [];
  younger.forEach((v) => {
    gcd.push(Math.abs(v - loca));
  });
  while (gcd.length !== 1) {
    gcd.push(getGCD(gcd.pop(), gcd.pop()));
  }
  return gcd.join('');
}

const getGCD = (num1, num2) => {
  let [b, s] = num1 < num2 ? [num2, num1] : [num1, num2];

  while (b % s !== 0) {
    [b, s] = [s, b % s];
  }

  return s;
};