그래프
정점과 간선으로 구성되어 네트워크 구조를 추상화한 비선형 자료 구조
특징
- 정점(node)과 간선의 집합
- 다양한 그래프 종류를 혼합하여 표현 가능
- 길찾기, 게임, 지도, 네비, 네트워크 등 다양한 곳에서 사용 가능
그래프 종류
- 방향 그래프 (Directed Graph): 간선에 특정 방향이 존재하는 그래프 (A→ B로 표현, A에서 B로만 이동 가능)
- 무방향 그래프 (Undirected Graph): 간선에 특정 방향이 존재하지 않는 그래프 (A - B로 표현, 양방향 이동 가능)
- 가중치 그래프 (Weighted Graph): 간선에 비용이나 가중치가 할당된 그래프

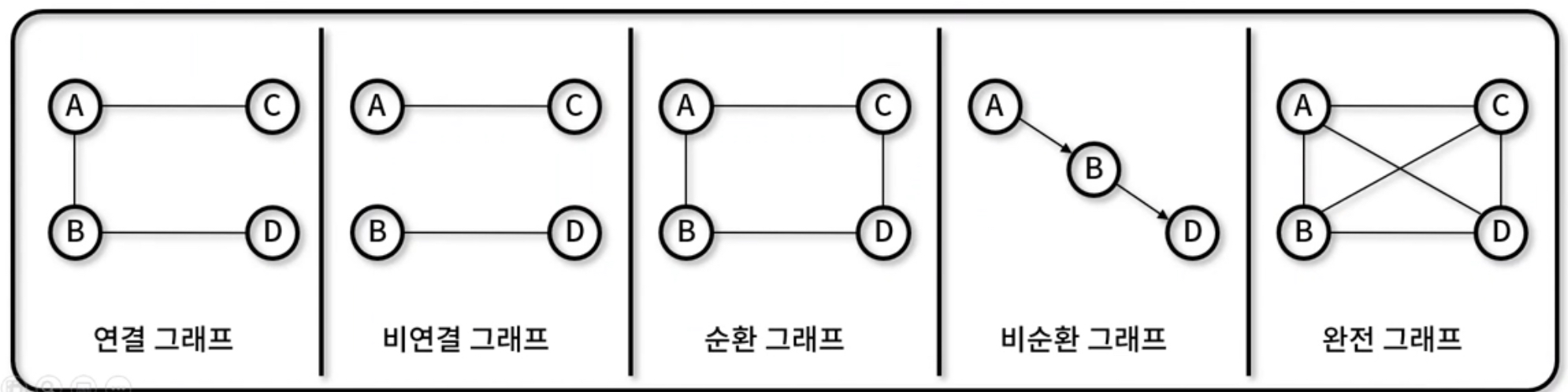
- 연결 그래프 (Connected Graph): 무방향 그래프에 있는 모든 정점쌍에 대해 항상 경로가 존재하는 그래프
- 비연결 그래프 (Disconnected Graph): 무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 그래프
- 순환 그래프 (Cycle): 단순 경로의 시작 정점과 종료 지점이 동일하여 순환 지점이 존재하는 그래프
- 비순환 그래프(Acyclic Graph): 순환 지점이 존재하지 않는 그래프
- 완전 그래프 (Complete Graph): 그래프에 속해 있는 모든 정점이 서로 연결되어 있는 그래프
그래프 표현 방법
- 인접 리스트 (Adjacency List): 정점에 연결된 다른 정점을 리스트로 표현
- 인접 행렬 (Adjacency Matrix): 정점에 연결된 다른 정점을 정점 X 정점 크기의 매트릭스로 표현
구현 메서드
- 정점/간선 추가: Graph.addVertex(), Graph.addEdge()
- 정점/간선 삭제: Graph.removeVertex(), Graph.removeEdge()
- 정점/간선 개수, 그래프 출력: Graph.sizeVertex(), Graph.sizeEdge(), Graph.print()
1. 인접리스트로 그래프 표현
2. 정점 및 간선 추가 (addVertex(), addEdge())
정점의 경우 Node를 의미하며, 간선은 Node끼리의 연결을 의미한다.
- addVertex를 통해 this.edge라는 객체에 정점을 추가한다.
- addEdge를 통해 정점 사이의 간선을 추가한다.
class Graph {
constructor() {
this.edge = {};
}
addVertex(v) {
this.edge[v] = [];
}
addEdge(v1,v2) {
this.edge[v1].push(v2);
}
}3. 정점 및 간선 삭제 (removeVertex(), removeEdge())
- removeEdge는 해당하는 vertex가 있는지 확인한 후 index를 찾아 삭제하고, 만약 남아있는 vertex의 length가 0이라면 해당 정점을 삭제한다.
- removeVertex는 해당하는 vertex의 Edge를 removeEdge한다.
removeVertex(v) {
if (this.edge[v] === undefined) return;
let length = this.edge[v].length;
let connectedVertex = [...this.edge[v]];
for (let i = 0; i < length; i++) {
this.removeEdge(v, connectedVertex[i]);
}
}
removeEdge(v1, v2) {
if (this.edge[v1]) {
let idx = this.edge[v1].indexOf(v2);
if (idx != -1) {
this.edge[v1].splice(idx, 1);
}
if (this.edge[v1].length === 0) {
delete this.edge[v1];
}
}
}4. 정점의 개수 및 간선의 개수 반환 (sizeVertex(), sizeEdge())
- sizeVertex는 Object 내부 함수를 사용해서 해당 key의 length를 구한다.
- sizeEdge는 this.edge[vertex] 여부를 확인하여 true일 경우, Object.keys(this.edge[vertex].length)
sizeVertex () {
return Object.keys(this.edge).length;
}
sizeEdge (vertex) {
return this.edge[vertex] ? Object.keys(this.edge[vertex].length) : 0;
}5. print()
print () {
for (let vertex in this.edge) {
let neighbors = this.edge[vertex];
if (neighbors.length === 0) continue;
process.stdout.write(`${vertex} -> `);
for (let i = 0; i < neighbors.length; ++i) {
process.stdout.write(`${neighbors[i]} `);
}
console.log("");
}
}만약 무방향 그래프일 경우
- Edge에서 두 방향을 모두 연결시켜준다.
- removeEdge를 할 때 모든 방향을 모두 삭제한다.
addEdge(v1,v2) {
this.edge[v1].push(v2);
this.edge[v2].push(v1);
}removeEdge(v1, v2) {
if (this.edge[v1]) {
let idx = this.edge[v1].indexOf(v2);
if (idx != -1) {
this.edge[v1].splice(idx, 1);
}
if (this.edge[v1].length === 0) {
delete this.edge[v1];
}
}
if (this.edge[v2]) {
let idx = this.edge[v2].indexOf(v1);
if (idx != -1) {
this.edge[v2].splice(idx, 1);
}
if (this.edge[v2].length === 0) {
delete this.edge[v2];
}
}
}관련 전체 코드는 Git에 업로드 해두었습니다.
Github_Graph
Github_Graph No Direction
