이진 탐색 트리

나동빈님의 책과 유튜브 강의인 '이것이 코딩 테스트다'를 바탕으로 스스로 공부한 내용을 정리한 글입니다.
참고한 영상의 링크는 아래와 같습니다.
이것이 코딩테스트다 - 트리 알고리즘

---

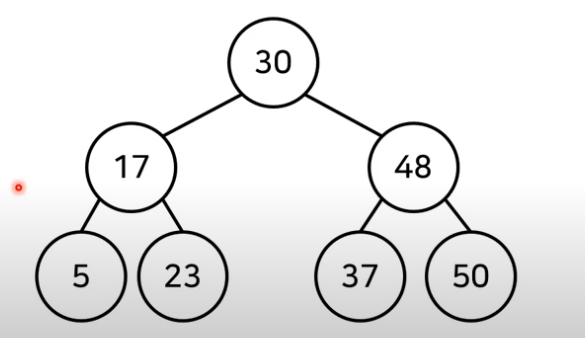
이진 탐색 트리

이진 탐색 트리는 아래 그림과 같은데, 다음과 같은 특징을 가진다.

• 부모 노드보다 왼쪽 자식 노드가 작다.
• 부모 노브보다 오른쪽 자식 노드가 크다.
• 이진 탐색 트리에서 탐색시간이 O(LogN)을 보장하려면 트리가 균형잡혀야 한다.

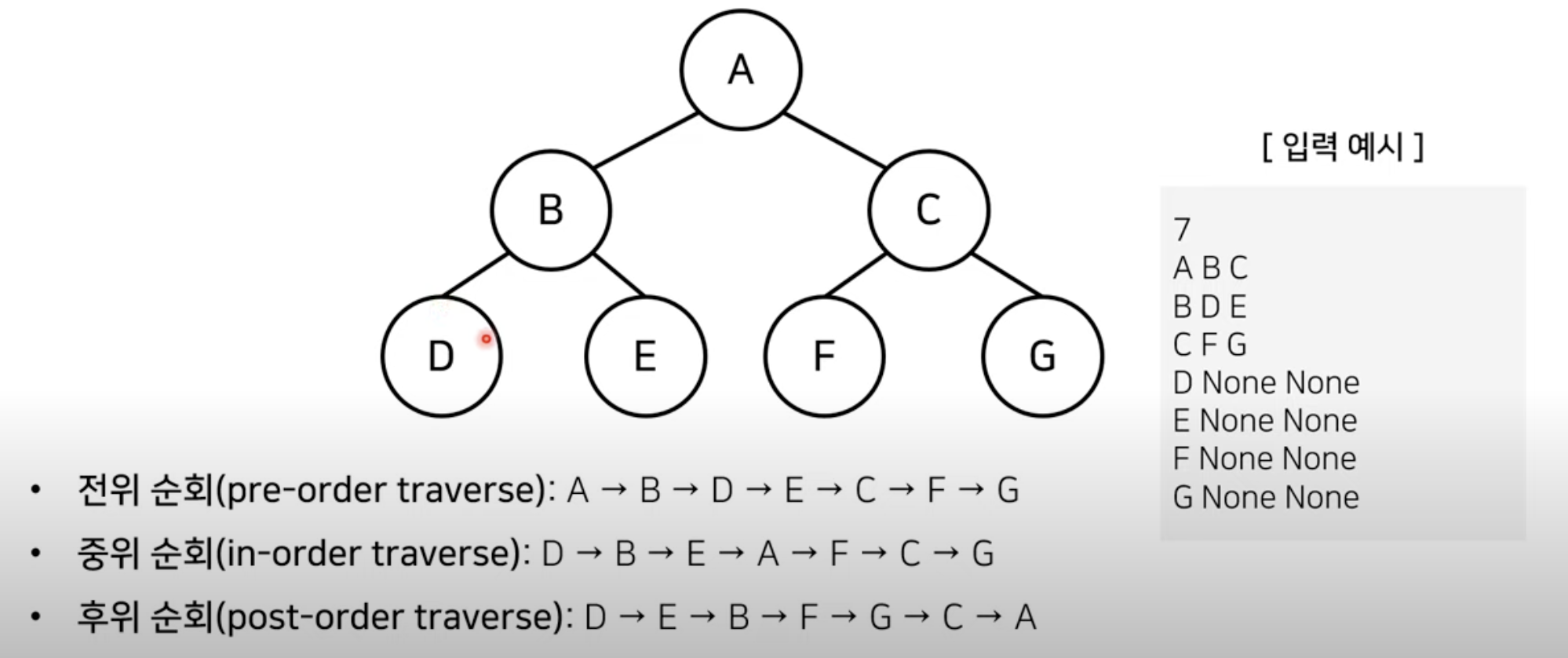
트리의 순회

• 트리 구조에 포함된 대표적인 순회 방법은 다음과 같다.

1. 전위 순회 (pre-order traverse): 부모 노드를 먼저 방문한 후, 왼쪽 자식 > 오른쪽 자식 노드를 방문 하는 방법
2. 중위 순회 (in-order traverse): 왼쪽 자식 방문 이후 부모 노드 방문, 이후 오른쪽 노드를 방문 하는 방법
3. 후위 순회 (post-order traverse): 왼쪽 자식 방문 > 오른쪽 자식 방문 이후 > 부모 노드를 방문 하는 방법

순회 방법을 헷갈리지 않는 방법은 제목에 모든 KEY가 있다.
원칙: 항상 왼쪽 자식 > 오른쪽 자식의 방문순서는 고정이다
pre / in / post는 부모노드의 방문순서가 어디에 있을지 정해준다. (e.g., pre일 경우에는 부모 > 왼쪽 자식 > 오른쪽 자식)

class Node:

  def __init__(self, data, left_node, right_node):
    self.data = data
    self.left_node = left_node
    self.right_node = right_node


n = int(input())
tree = {}

for i in range(n):
  data, left_node, right_node = input().split()
  if left_node == 'None':
    left_node = None
  if right_node == 'None':
    right_node = None
  tree[data] = Node(data, left_node, right_node)


def pre_order(node):
  print(node.data, end=" ")
  if node.left_node != None:
    pre_order(tree[node.left_node])
  if node.right_node != None:
    pre_order(tree[node.right_node])


def in_order(node):
  if node.left_node != None:
    in_order(tree[node.left_node])
  print(node.data, end=" ")
  if node.right_node != None:
    in_order(tree[node.right_node])


def post_order(node):
  if node.left_node != None:
    post_order(tree[node.left_node])
  if node.right_node != None:
    post_order(tree[node.right_node])
  print(node.data, end=" ")


pre_order(tree['A'])
print()
in_order(tree['A'])
print()
post_order(tree['A'])
print()

!!Tree 상에서 이동하는 tree[node.left/rigt_node]를 헷갈려서 시간을 좀 허비했다.. 다음부터는 사소한 곳에서 헷갈리지 말도록 하자!