
이번 글에 있는 내용을 익힌 후 이 글의 라이브러리를 사용하면 편하게 데이터 관계를 분석할 수 있습니다.
설치 -%pip install rock-pre-h
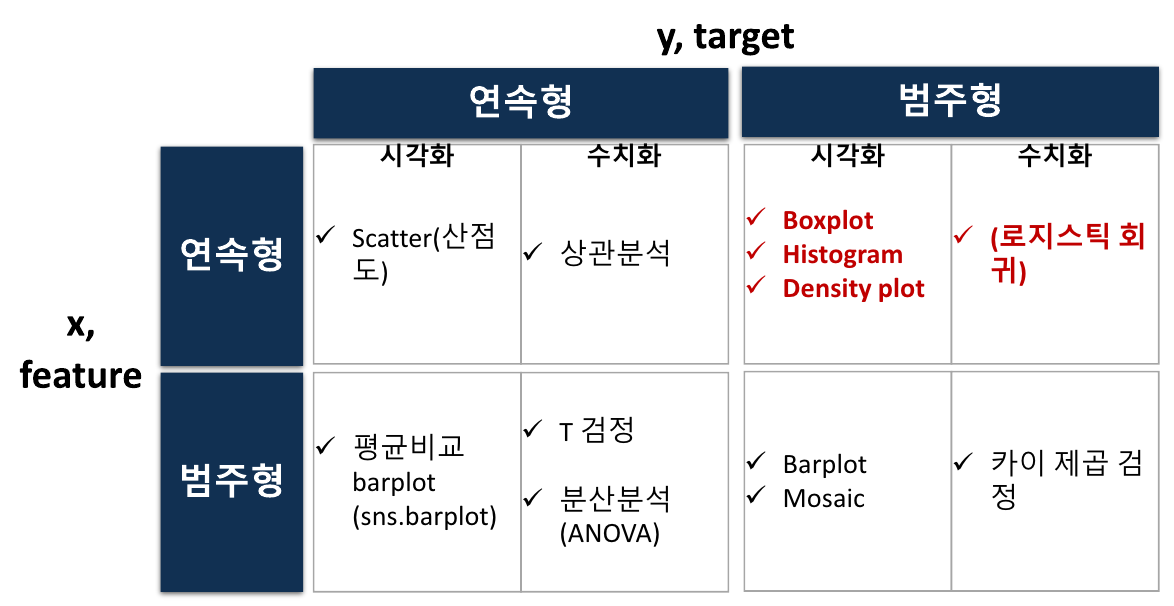
두 변수의 관계 분석하기
(뮤) = 모평균
(시그마 제곱) = 모분산
= 표본평균
= 표본분산
숫자 -> 숫자
라이브러리 임포트
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler, StandardScaler
import warnings
warnings.filterwarnings( 'ignore' )
import scipy.stats as spst
titanic = pd.read_csv('titanic.csv')
titanic.drop('Cabin', axis = 1, inplace = True)
titanic.dropna(axis = 0, inplace = True) # 결측치 제거 필수
titanic산점도
plt.scatter(titanic['Age'], titanic['Fare'])
plt.show()
spst.pearsonr(titanic['Age'], titanic['Fare']) # 왼쪽 상관계수, 오른쪽 p-value
titanic.corr() # 타이타닉의 모든 데이터의 상관계수를 다 구해줌
plt.figure(figsize = (16, 16)) # 상관계수 heatmap 그리는법
mask = np.zeros_like(titanic.corr(), dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
sns.heatmap(titanic.corr(), annot = True, fmt = '.3f', mask = mask, cmap = 'RdYlBu_r', vmin = -1, vmax = 1) # fmt는 e+05로 표시되는거 바꿔줌
plt.show()범주 -> 숫자
선행개념
- 중심극한정리 : 모집단이 어떻게 생겼든 n만큼의 값을 뽑아서 평균을 내고 그걸 충분히 많은 n회 반복하면 그 평균들의 분포는 정규분포를 따른다
- 표준편차는 std(), 표준오차는 sem()
# 대립가설이 생존여부에 따른 나이의 차이가 있다 일때
sns.barplot(x = 'Survived', y = 'Age', data = titanic)
# 결과에서 신뢰구간이 안겹치면 평균의 차이가 있다는 뜻, 많이 겹치면 반대
# 평균의 차이가 클수록 서로 연관이 있음T 통계량
- 두 평균의 차이를 표준오차로 나눈 값, 기본적으로는 두 평균의 차이로 이해해도 됨
- 일반적으로 t값이 -2 > t, t > 2면 차이가 있다고 봄
died = titanic.loc[titanic['Survived'] == 0, 'Age']
Survived = titanic.loc[titanic['Survived'] == 1, 'Age']
spst.ttest_ind(died, Survived) # statistic=2.2043427748445956, 관련이 있긴한데 거의 없다ANOVA
P_1 = titanic.loc[titanic['Pclass'] == 1, 'Age']
P_2 = titanic.loc[titanic['Pclass'] == 2, 'Age']
P_3 = titanic.loc[titanic['Pclass'] == 3, 'Age']
sns.barplot("Pclass","Age", data = titanic)
spst.f_oneway(P_1, P_2, P_3) # 일반적으로 f 통계량 값이 2 ~ 3 이상이면 차이가 있다고 판단범주 -> 범주
100% stacked barplot, mosaic plot
# normalize쓰면 비율로 바꿔줌, 비율만 가지고 비교하므로 양에 대한 비교를 할 수 없음
temp12 = pd.crosstab(titanic['Survived'], titanic['Sex'], normalize = 'index')
# 위로 쌓아서 그래프를 그림
temp12.plot.bar(stacked = True)
# 전체 평균 선
plt.axhline(1-titanic['Survived'].mean(), color='r')
plt.show()from statsmodels.graphics.mosaicplot import mosaic
mosaic(titanic, ['Pclass', 'Survived'])
plt.axhline(1-titanic['Survived'].mean(), color='r') # 전체 평균 선, 멀리 떨어져 있을 수록 연관이 있음
plt.show()(카이 제곱) 검정
- 귀무가설이 기대되는 빈도 --> 서로 관련이 없으면 수치가 증가
table = pd.crosstab(titanic['Survived'], titanic['Pclass'])
result = spst.chi2_contingency(table)
print('카이제곱통계량:', result[0])
print('p-value:', result[1])
print('기대빈도:', result[2]) # 보통 카이제곱 통계량은 자유도의 2~3배 보다 크면 차이가 있다고 봄
# 자유도는 Pclass = 2, Survived = 1숫자 -> 범주 (크게 중요하진 않음 참고 정도만)
sns.histplot(x = 'Age', data = titanic, hue = 'Survived')
plt.show()sns.kdeplot(x = 'Age', data = titanic, hue = 'Survived', multiple = 'fill')
plt.axhline(titanic['Survived'].mean(), color = 'r')
plt.show()
# 빨간선은 평균, 생존율이 1에 가까울 수록 생존율이 전체 평균보다 높다는 뜻, 아니면 반대
# 빨간선(평균)을 기준으로 많이 빠져나올 수록 서로 관련이 있음