[Gold I][JAVA]1003번: K번째 수

https://www.acmicpc.net/problem/1300

알고리즘

3 3

N차원 배열

=

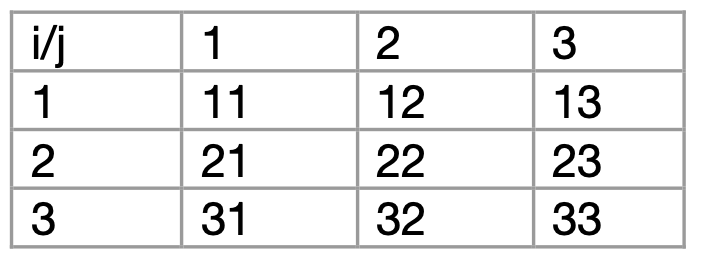
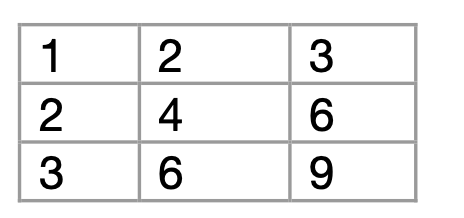
이때, 6이라는 숫자가 오름차순 정렬되었을때 몇 번째에 오는지 알아보자.
• 1번열은 모두 6이하 이므로 3을 더해준다.
• 2번열은 모두 6이하 이므로 3을 더해준다.
• 3번열은 3, 6 두개의 숫자가 6이하 이므로 2를 더해준다.

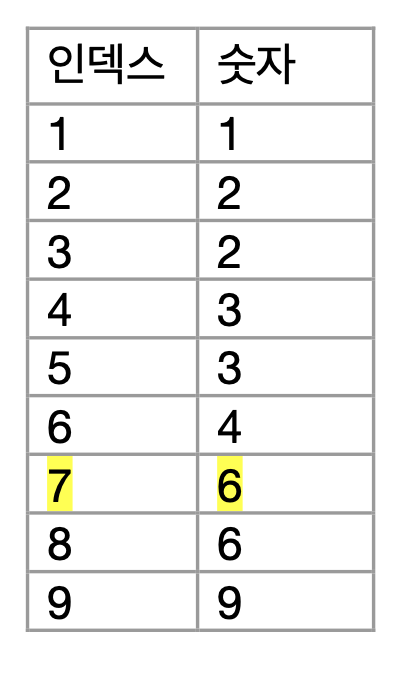
• 첫 번째 열(1, 2, 3)은 1의 배수이다. 해당 열에서 표현할 수 있는 6이하의 최대 수는 6개이다. (6/1=6)
• 두 번째 열(2, 4, 6)은 2의 배수이다. 해당 열에서 표현할 수 있는 6이하의 최대 수는 3개이다. (6/2=3)
• 세 번째 열(3, 6, 9)은 3의 배수이다. 해당 열에서 표현할 수 있는 6이하의 최대 수는 2개이다. (6/3=2)

계산 방법

행렬의 원소는 i의 배수에 해당한다.

cnt = min(mid / i, N) -> mid는 임의의 수, i는 i번째 줄을 의미.
left = 1, right = K로 두고, left <= right일 때까지 while문을 진행하면서 위 식에 따라서 cnt를 계산한 후, cnt와 K를 비교하면서 left 혹은 right를 초기화하는 것입니다.

코드

package baekjoon_java.GoldI;

import java.io.*;

public class K번째수 {//1300번 이분탐색

    public static void main(String arg[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int N = Integer.parseInt(br.readLine());
        int K = Integer.parseInt(br.readLine());

        long left = 1, right = K;
        long ans = 0;

        // 이분 탐색 수행
        while (left <= right) {
            long mid = (left + right) / 2; // 임의의 수 지정
            long cnt = 0;

            // mid보다 작거나 같은 수는 몇 개인지 계산.
            for (int i = 1; i <= N; i++) {
                cnt += Math.min(mid / i, N);
            }

            if (cnt < K) {
                left = mid + 1;
            } else {
                ans = mid;
                right = mid - 1;
            }
        }
        bw.write(ans + "\n");
        bw.flush();
        bw.close();
        br.close();
    }
}