[Silver V][JAVA] 1417번:국회의원선거

이 문제를 만족시키기 위해서 어떻게 해야할지부터 생각해보자. 다솜이가 처음 얻은 듣표수를 a라고 하겠다. 그럼 그 나머지 득표수들을 -시키면서, a를 +시켜나갈 때 나머지 득표수 중 가장 큰 득표수보다 a가 커지면 된다.

그렇다면 중요한 요소는 나머지 득표수 중 가장 큰 득표수이다. 이걸 max라 하겠다. 결국 매번 max값을 -1 시키고, a를 +1 시켜나가면 원하는 답을 구할 수 있다. 예를들어 다음의 경우를 보자.

4
1
3
3
4

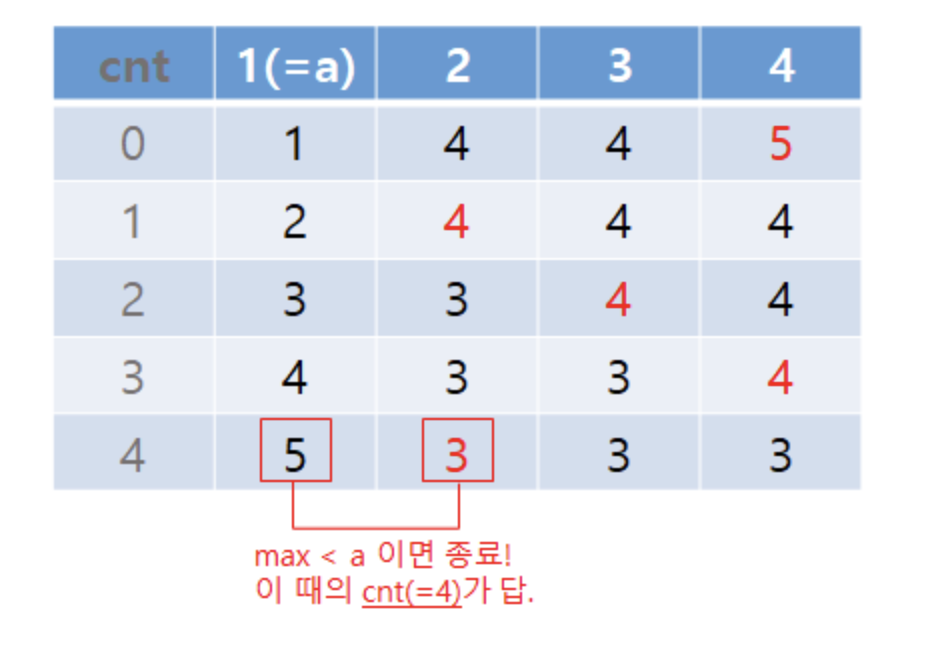
답을 찾는 과정은 다음과 같다. 매번 max값을 찾고(빨간색으로 나타냈다), 해당 값을 -1 시키고 a를 +1 시킨다. 그러다가 max<a이면 답을 출력하면 된다!

위와 같이 배열에 값들을 두고 매번 max값을 찾거나 정렬하면서 진행하면 된다. 즉 시뮬레이션을 돌리는 것이다. 이 경우 시간복잡도는 대략 O(N^2) 정도 된다(정렬시엔 O(N^2logN). 사실 총 득표수 합에 비례하긴 하지만 어차피 제한이 적어 크게 차이 안나므로 대강 N으로 나타냈다.). 애초에 제한이 아주 작아서 이렇게 해도 매우 빠른 시간 안에 찾을 수 있다.

이 경우 간단하게 최대 힙을 사용하면 좀 더 효율적으로 짤 수 있다. 이 경우 max 값을 찾을 때 O(logN)으로 가능하다. 따라서 총 O(NlogN)의 효율성을 가진다.

매수를 진행한 횟수를 결과로 출력합니다.
BufferedReader를 사용하여 입력되는 정보를 저장합니다.
PriorityQueue를 사용하여 다른 후보들의 투표수가 가장 큰 값을 가져옵니다.
다솜이가 당선될 때까지 매수를 진행합니다.
매수를 진행한 횟수를 결과로 BufferedWriter에 저장하였습니다.
BufferedWriter에 저장된 결과값을 출력하였습니다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Collections;
import java.util.PriorityQueue;

public class 국회의원선거 {
    private void solution() throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int a = Integer.parseInt(br.readLine());
        //다른 후보 투표수 내림차순 우선순위 큐
        PriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder());

        //다른 후보 투표수 저장
        while (n-->1) pq.add(Integer.parseInt(br.readLine()));
        int cnt = 0;

        //다른 후보의 사람들 매수 진행
        while (!pq.isEmpty() && pq.peek() >= a) {
            cnt++;
            a++;//매수 횟수 +1
            pq.add(pq.poll()-1);//가장 큰 후보 투표수 -1
        }
        System.out.println(cnt);
    }

    public static void main(String[] args) throws Exception {
        new 국회의원선거().solution();
    }
}