Two-Pointers Algorithm (투 포인터 알고리즘)

투 포인터

배열에서 원래 이중 for문으로 O(N^2)에 처리되는 작업을 2개 포인터의 움직임으로 O(N)에 해결하는 알고리즘

리스트에 순차적으로 접근하여 두 개의 위치를 기록하며 처리
부분 연속 수열 문제에 사용
시간 복잡도 O(N)으로 처리 가능 ( 시간 복잡도를 O(n^2) 에서 최대 O(n) 까지 줄일 수 있습니다.)

순서

투 포인터에서, 2. 둘 다 첫 번째 원소에서 시작하는 경우를 사용하였습니다.
start = 0, end = 0 으로 시작합니다. 투 포인터는 start <= end 여야 합니다.

start < n까지 반복합니다.
1. 구간 합(sum)이 M을 초과하거나, end가 배열의 범위를 넘으면
sum-arr[start] , start 오른쪽 한칸 이동을 해줍니다.
2. 구간 합(sum)이 M과 같거나 이하일때, end가 배열의 범위를 넘지 않을 때
sum+arr[end] , end 오른쪽 한칸 이동 해줍니다.
만약 구간합(sum)이 M과 같다면 결과(count)를 증가시켜줍니다.

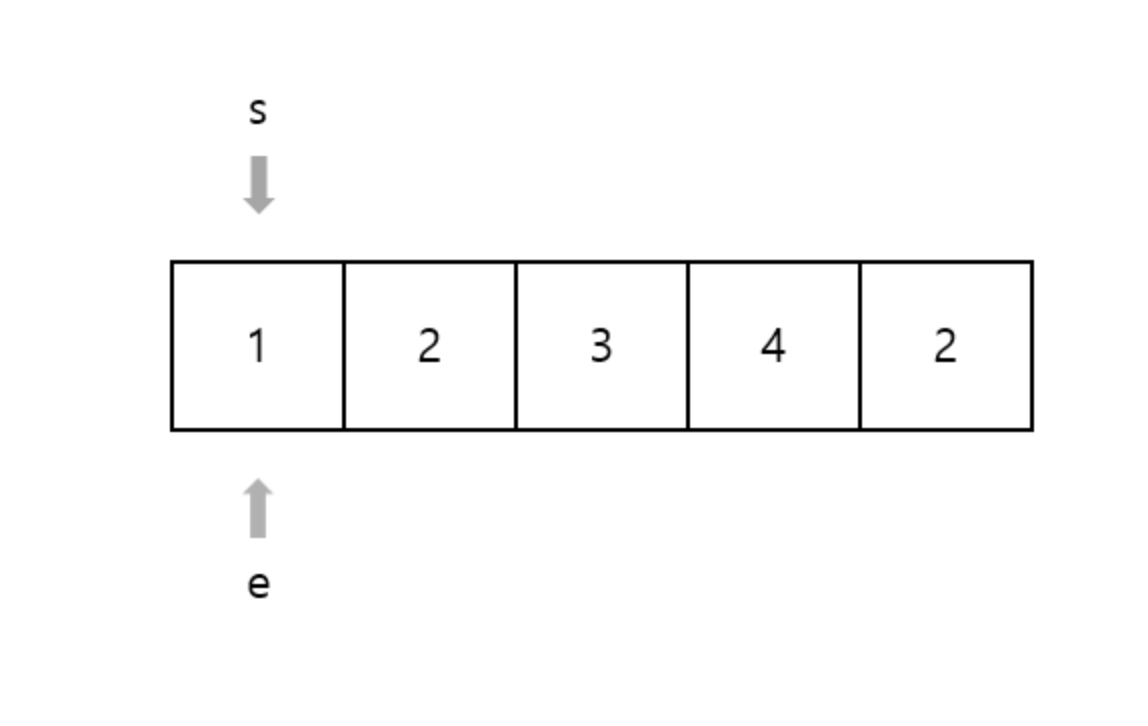
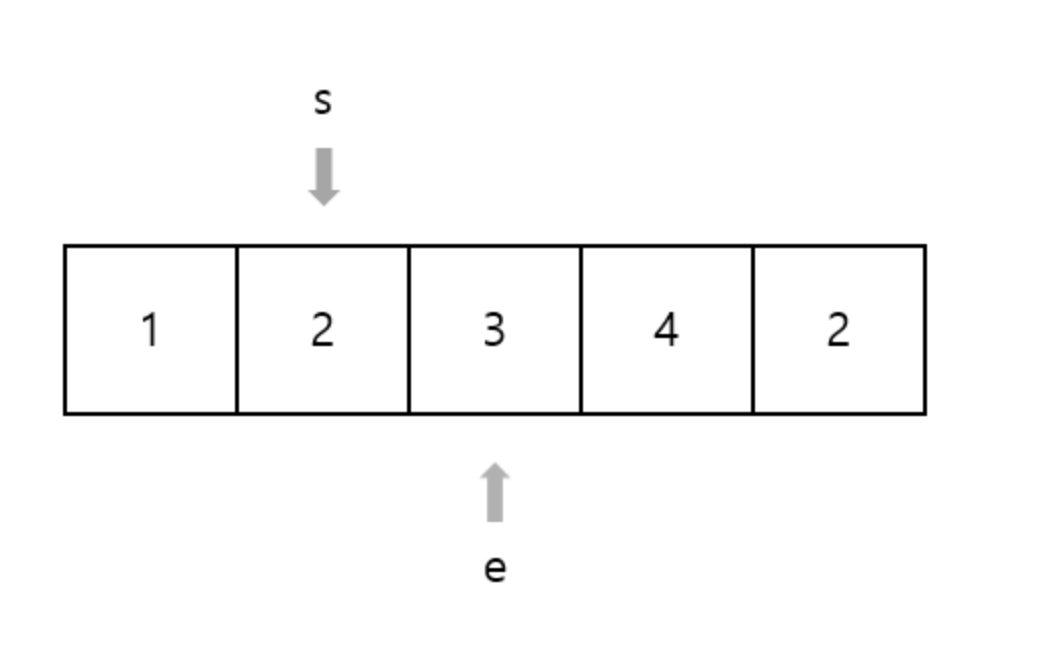
다음과 같은 배열에서 합이 M = 5 인 부분 수열 개수 찾기

S, E 포인터 위치를 배열의 처음에 두고 시작한다.

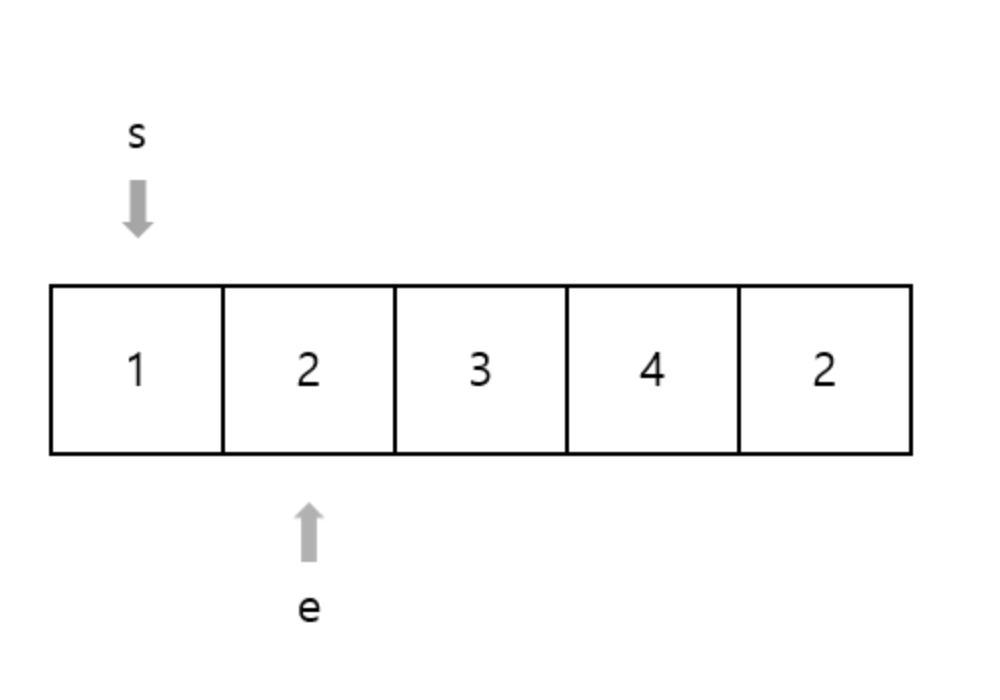
E 포인터를 계속 이동하면서 E가 가리키는 값을 더한다.

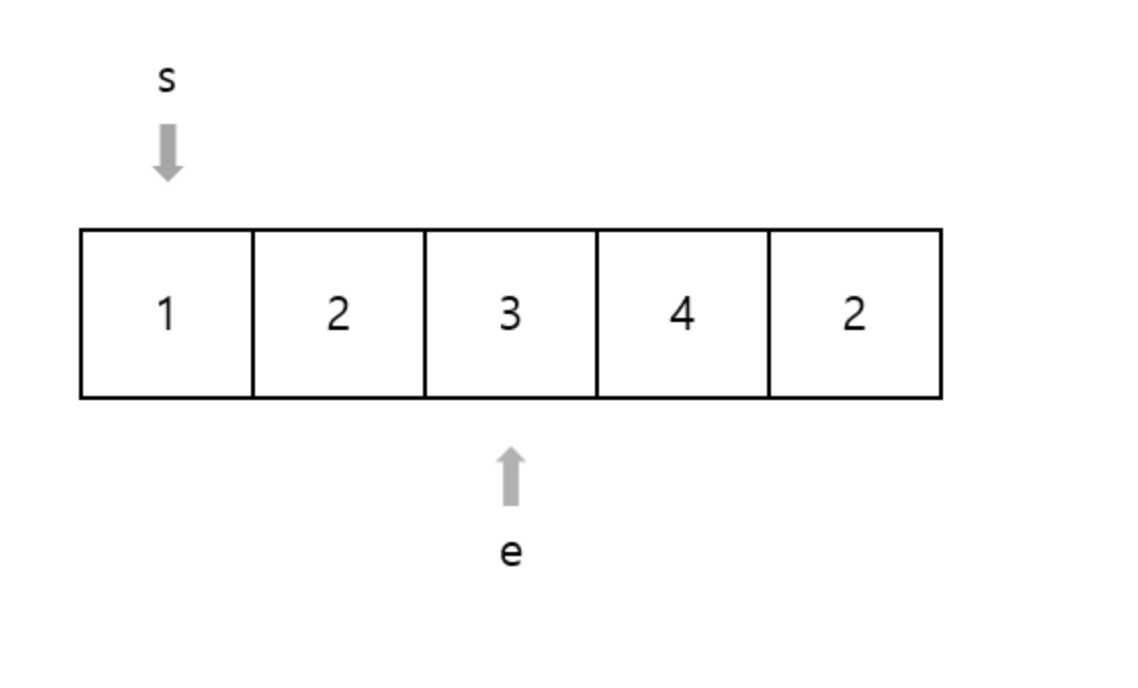
S 부터 E 까지의 합이 5 이상이되면 E는 이동을 멈춘다. 이 때, 합이 5라면 개수를 센다.
S를 한 칸 움직이고 S가 가리키던 값을 뺀다.

Java

public class boj_2003_수들의합2 { //투 포인터
    public static void main(String args[]) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());
        int[] arr = new int[N];

        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        int start = 0, end = 0, count = 0, sum = 0;
        while (start < N) {
            if (end < N && sum < M) sum += arr[end++];
            else sum -= arr[start++];

            if (sum == M)
                count++;
        }
        System.out.println(count);
    }
}

기본 문제

수들의 합 2 - ⚪️ 실버 4
백준 1806 부분합 - 🟡 골드 4
백준 1644 소수의 연속합 - 🟡 골드 3