그래프 탐색이란
하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
Ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지
깊이 우선 탐색이란
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
- 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
- 즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
- 사용하는 경우: 모든 노드를 방문 하고자 하는 경우에 이 방법을 선택한다.
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
- 단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.
깊이 우선 탐색(DFS)의 특징
- 자기 자신을 호출하는 순환 알고리즘의 형태 를 가지고 있다.
- 전위 순회(Pre-Order Traversals)를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.
- 이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다.
이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
깊이 우선 탐색(DFS)의 과정
1.정정 i를 방문한다,
2.정점 i에 인접한 정점 중에서 아직 방문하지 않은 정점이 있으면 이 정점을 모두 stack에 저장한다.
3.스택에서 정점을 삭제하여 새로운 i를 설정하고 다시 단계 1부터 수행한다,
4.스택이 공백이 되면 연산을 종료한다.
DFS (Depth-First Search, 깊이 우선 탐색) 알고리즘에 경우 두 가지 방법으로 풀 수 있다.
1) 스택을 이용하는 것이다.
2) 재귀함수를 이용하는 것인데, 재귀 함수의 코드가 훨씬 짧다.
3) 모든 경우의 수를 탐색하고자 하는 미로 문제가 같은 경우에 적합하다. 이유는 미로 문제는 최단 경로가 아닌 탈출하는 경로를 고려해야 하기 때문이다.
import java.util.Stack;
public class Main {
// Pair 클래스 정의
static class Pair {
int x, y;
Pair(int x, int y) {
this.x = x;
this.y = y;
}
}
static int[][] board = new int[502][502]; // 미리 크기를 설정한 이차원 배열 (board)
static boolean[][] vis = new boolean[502][502]; // 방문 여부 확인하는 배열
static int n = 7, m = 10;
static int[] dx = {1, 0, -1, 0}; // 방향 벡터 (상, 우, 하, 좌)
static int[] dy = {0, 1, 0, -1};
public static void main(String[] args) {
Stack<Pair> S = new Stack<>(); // 스택 선언
vis[0][0] = true; // (0, 0) 위치를 방문 처리
S.push(new Pair(0, 0)); // (0, 0) 시작점 추가
while (!S.isEmpty()) {
Pair cur = S.pop(); // 스택에서 현재 좌표 가져오기
System.out.println("(" + cur.x + ", " + cur.y + ") -> ");
for (int dir = 0; dir < 4; dir++) {
int nx = cur.x + dx[dir]; // 새로운 x 좌표
int ny = cur.y + dy[dir]; // 새로운 y 좌표
// 범위를 벗어나면 무시
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
// 이미 방문했거나, board[nx][ny]가 1이 아니면 무시
if (vis[nx][ny] || board[nx][ny] != 1) continue;
vis[nx][ny] = true; // 방문 처리
S.push(new Pair(nx, ny)); // 스택에 다음 좌표 추가
}
}
}
}Stack으로 이해하는 DFS
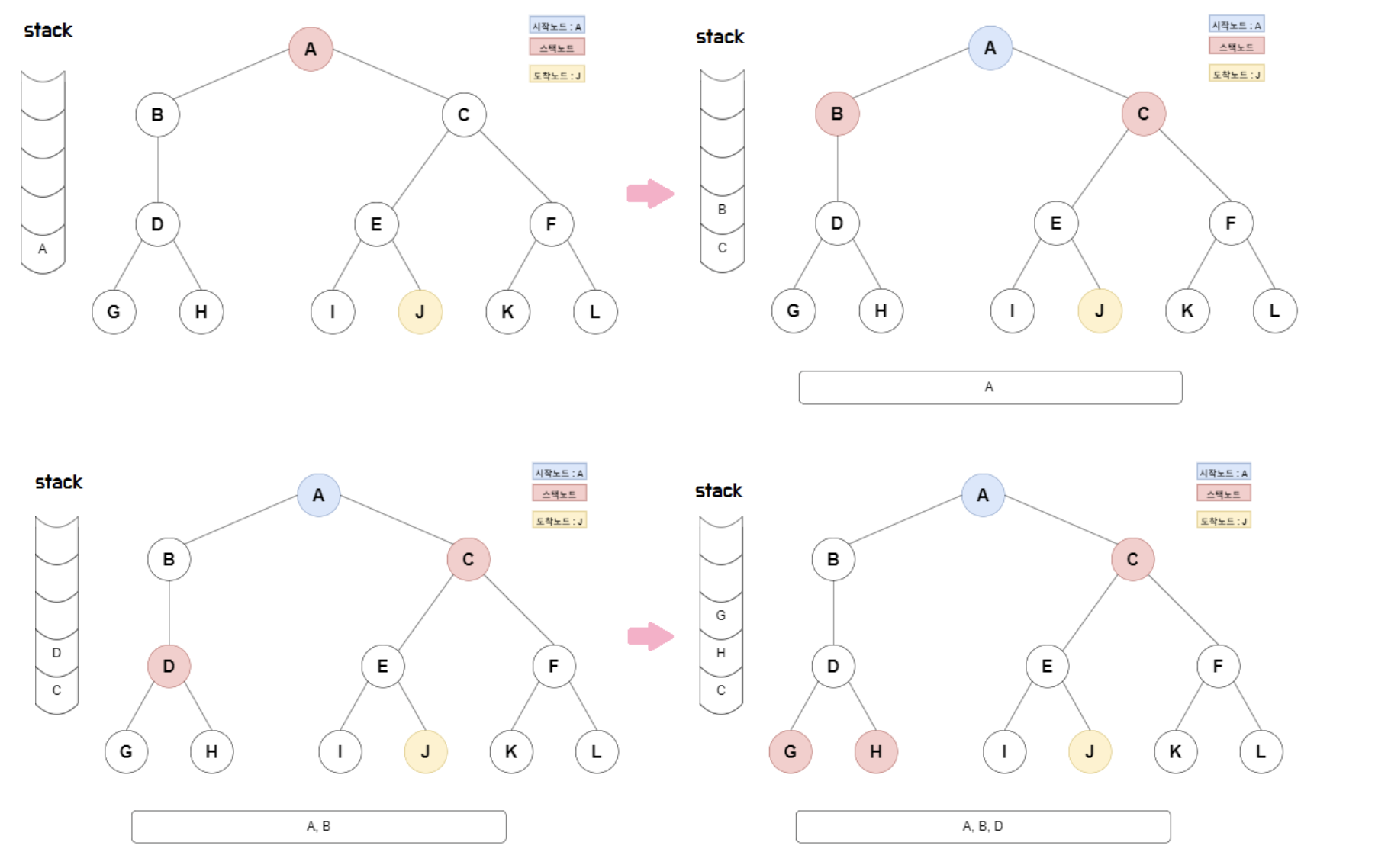
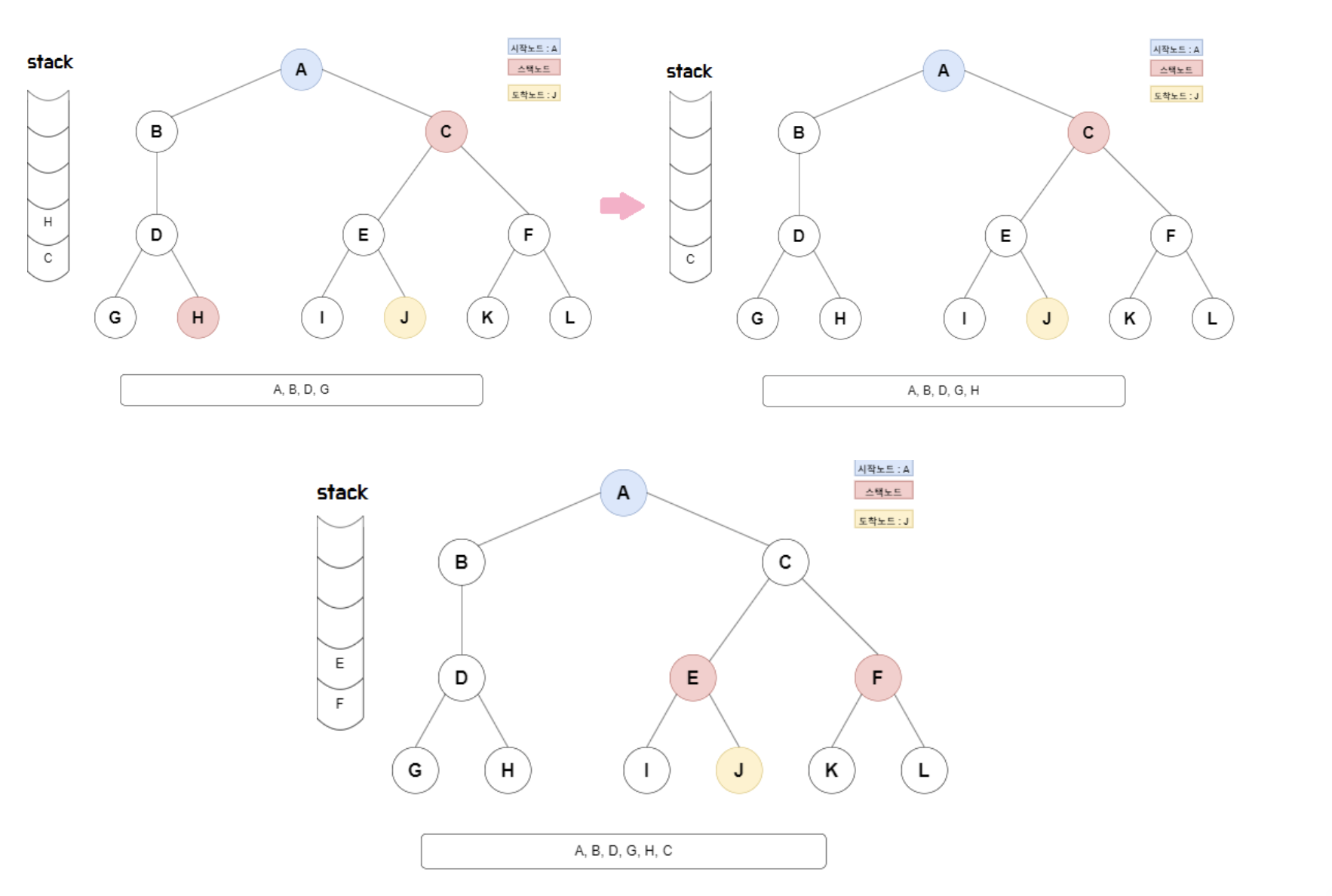
DFS 경로 => A, B, D, G, H, C