다익스트라(Dijkstra) -최단경로

키워드: 최단경로

다익스트라 알고리즘 = 하나의 시작점으로부터 다른 모든 정점까지의 최단 거리를 구하는 알고리즘

그래프 상에서 시작 정점부터 나머지 각 정점까지의 최단거리를 계산하는 알고리즘이다.

다익스트라 알고리즘 과정

1. 방문하지 않은 정점 중 가장 가중치 값이 작은 정점을 방문한다. (처음엔 시작 정점 방문)
2. 해당 정점을 거쳐서 갈 수 있는 정점의 거리가 이전에 기록한 값보다 작다면 그 거리를 갱신한다.

다익스트라 알고리즘의 탐색과정

우선순위 큐 방식

우선순위 큐를 이용한 다익스트라 알고리즘
1. 우선순위 큐에 (0, 시작점)을 추가
2. 우선순위 큐에서 거리가 가장 작은 원소를 선택, 해당 거리가 최단 거리 테이블에 있는 값과 다를 경우 넘어감
3. 원소가 가리키는 정점을 v라고 할 때, v와 이웃한 정점들에 대해 최단 거리 테이블 값보다 v를 거쳐가는 것이 더 작은 값을 가질 경우 최단 거리 테이블의 값을 갱신하고 우선순위 큐에 (거리, 이웃한 정점의 번호)를 추가
4. 우선순위 큐가 빌 때 까지 2, 3번 과정을 반복

다익스트라 알고리즘의 탐색 과정

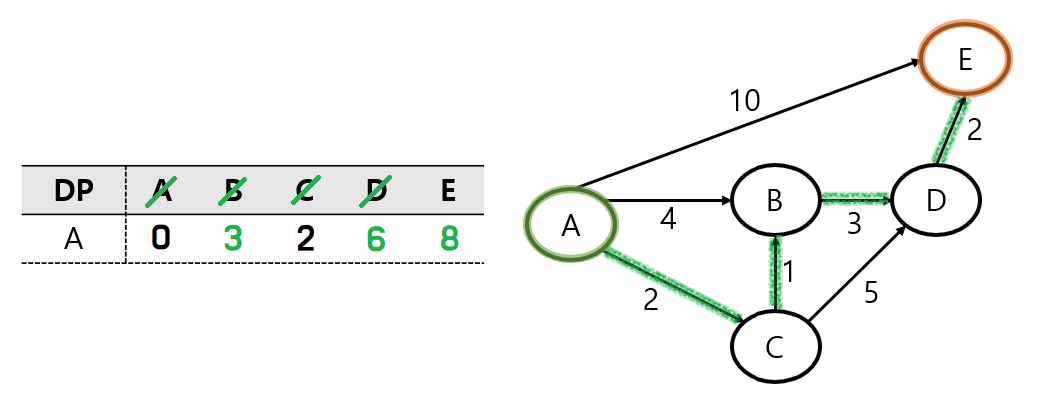
간단하게 A - E의 최단거리를 구하는 문제이다.

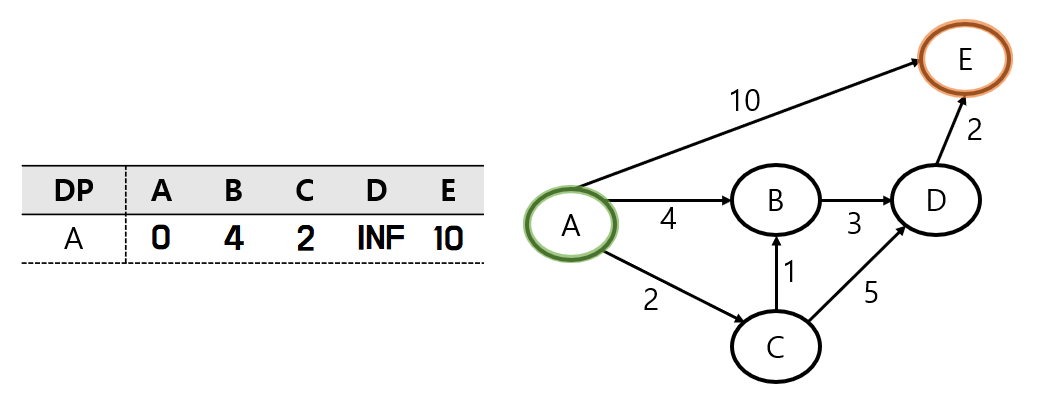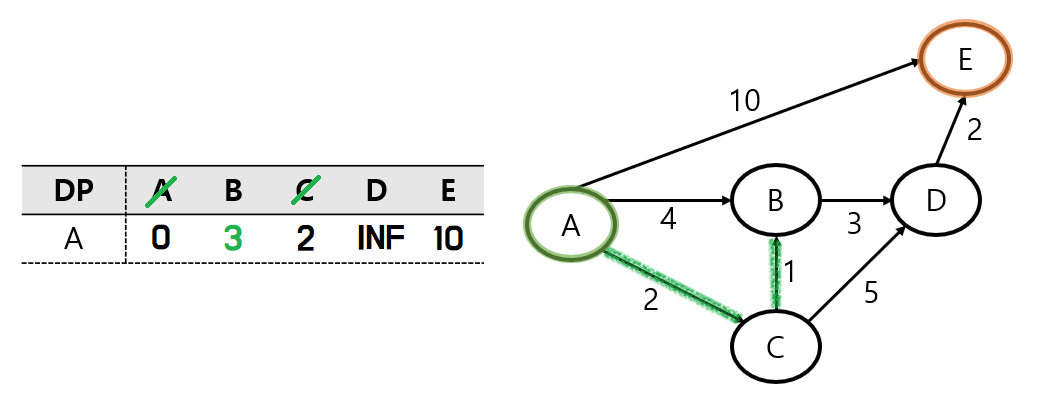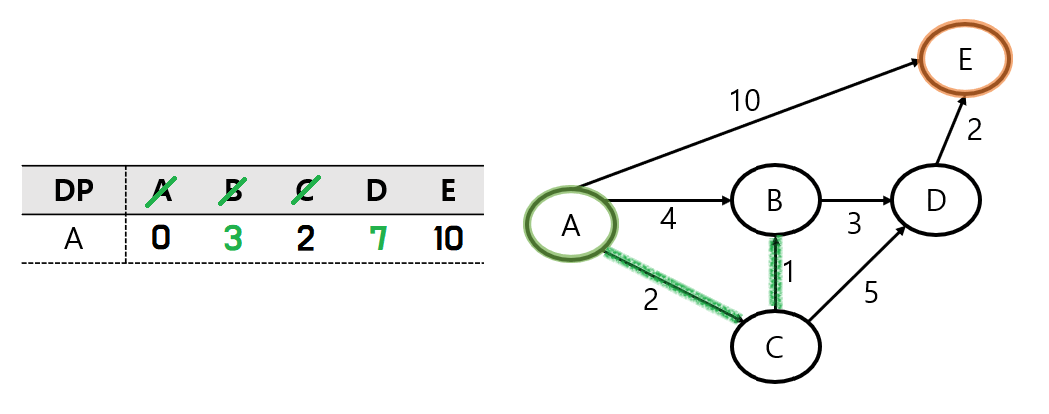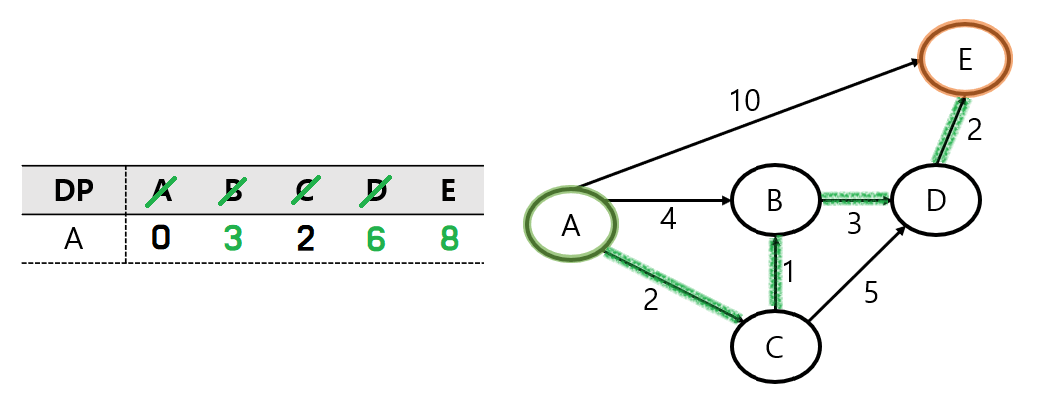
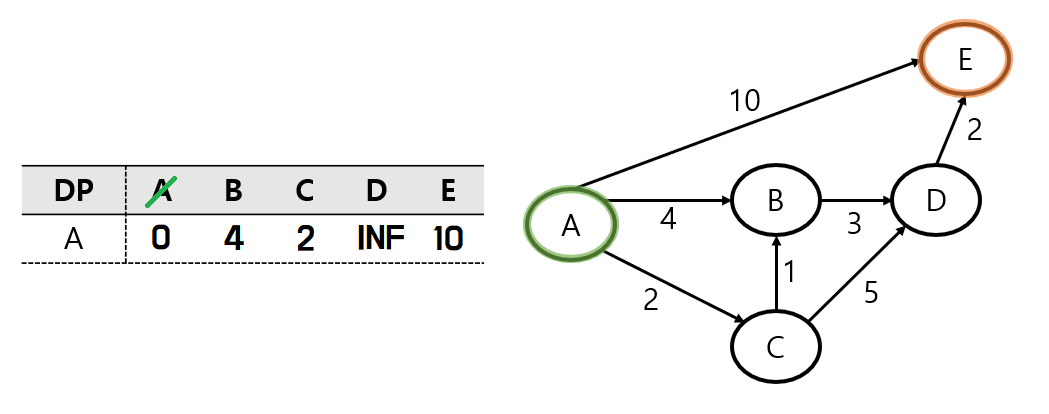
먼저 시작 노드인 A를 방문처리 해준다.

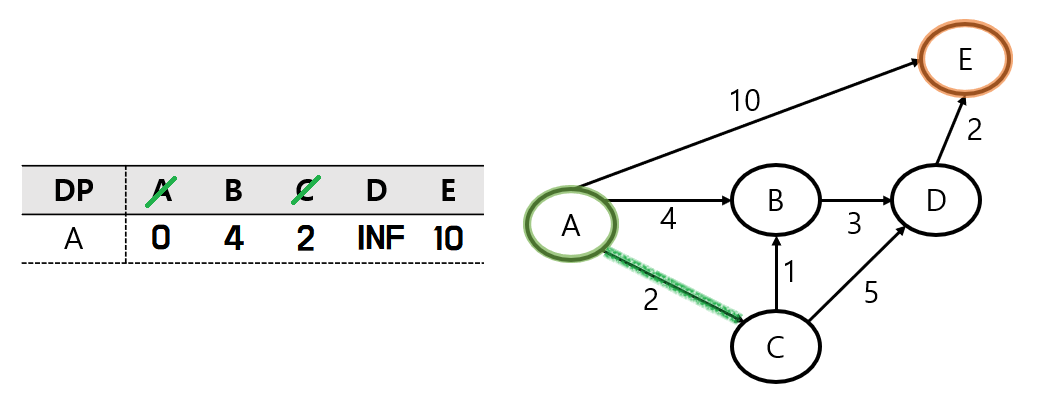
다음으로 시작 노드 A와 가장 가까이 위치한 C 노드로 이동하고, 방문처리한다.

이동한 C 노드에서는 B 노드와 D 노드로 이동을 할 수 있다.
먼저 B노드로 이동을 해보자.

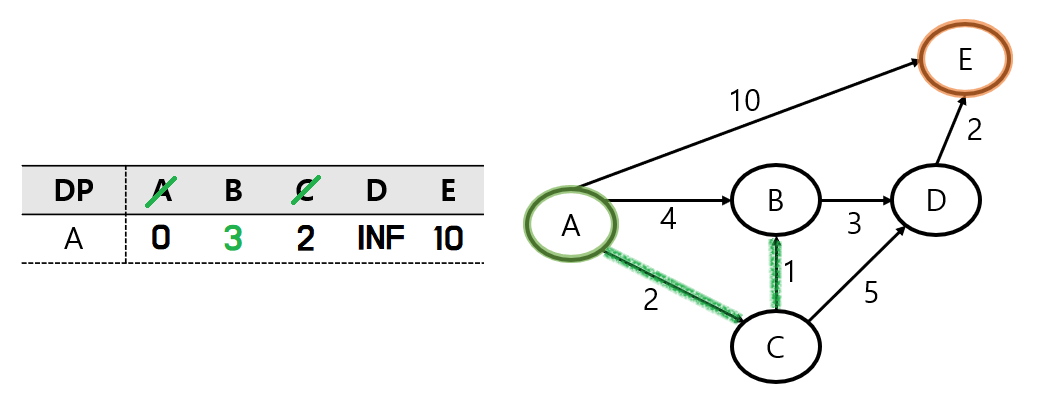
B 노드로 이동을 하게 되면,

DP에 저장된 값인 A - B 경로의 거리 4 보다
위의 그림의 초록색 길인 A - C - B 경로의 거리 3이 더 가까운 거리가 된다.

따라서 DP를 업데이트해 준다.

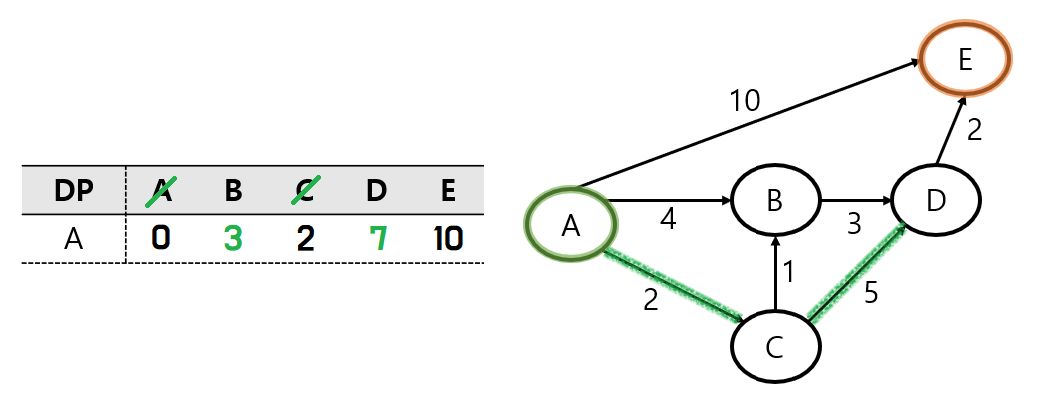
마찬가지로 C노드에서 D 노드로 가준다.

DP에 저장된 값인 A - D는 직접적으로 이동할 수 없는 값인 INF로 표현이 되어있다. (INF는 엄청 큰 수이다.)
이 값은, A - C - D의 경로를 이동한 7보다 큰 값이므로, DP를 업데이트해 준다.

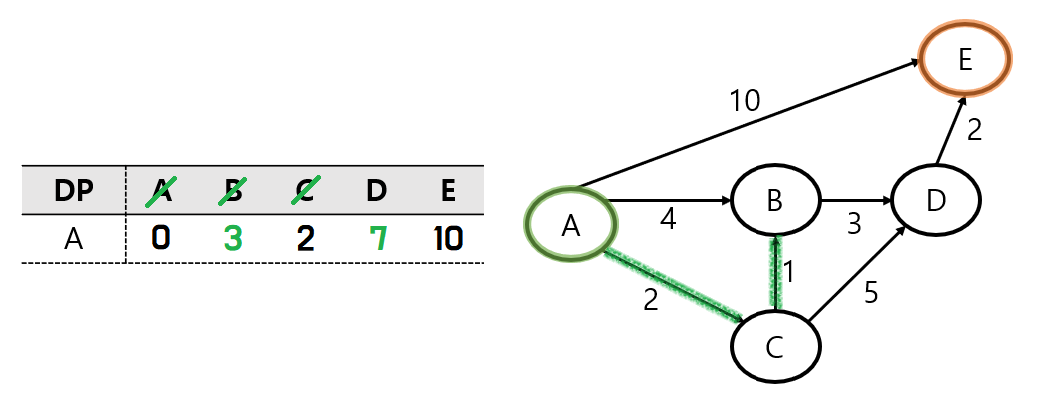
C 노드의 탐색이 끝났으므로, 다음으로 A노드와 가까운 노드인 B 노드를 탐색한다.

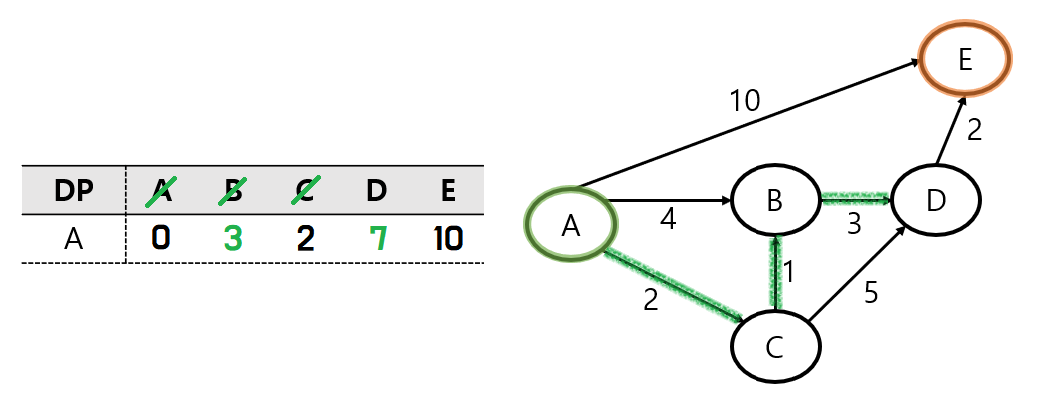
B 노드에서는 D노드로의 경로밖에 없다.

현재 DP에 저장되어 있는 A - D는 이전에 구해놓은 D까지의 최단거리이다.
하지만, B 노드에서 D 노드를 거치는 거리가 6으로 저장된 값보다 작기 때문에 업데이트해 준다.

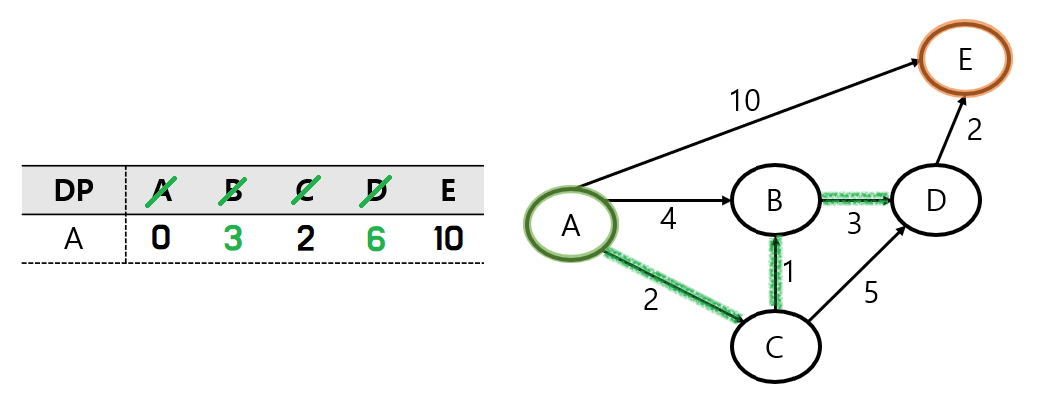
마찬가지로 D 노드를 방문처리하고, 위와 같은 방식으로 처리하면 최종 결과가 나오게 된다.

다익스트라 코드

https://www.acmicpc.net/problem/1753

import java.io.*;
import java.util.*;

public class boj_1916_최소비용구하기 {
    static final int INF = (int) 1e9 + 10;
    static int v, e, start;
    static ArrayList<ArrayList<Pair>> adj = new ArrayList<>();
    static int[] d = new int[20005];

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        v = Integer.parseInt(st.nextToken());
        e = Integer.parseInt(st.nextToken());

        st = new StringTokenizer(br.readLine());
        start = Integer.parseInt(st.nextToken());

        for (int i = 0; i <= v; i++) {
            adj.add(new ArrayList<>()); //그래프 초기화
        }

        Arrays.fill(d, 0, v + 1, INF);

        for (int i = 0; i < e; i++) {
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
            adj.get(u).add(new Pair(w, v));
        }

        PriorityQueue<Pair> pq = new PriorityQueue<>(Comparator.comparingInt(p -> p.cost));
        d[start] = 0;
        pq.offer(new Pair(0, start));

        while (!pq.isEmpty()) {
            Pair cur = pq.poll();
            int curCost = cur.cost;
            int curVertex = cur.vertex;

            if (d[curVertex] != curCost) continue;

            for (Pair nxt : adj.get(curVertex)) {
                if (d[nxt.vertex] > d[curVertex] + nxt.cost) {
                    d[nxt.vertex] = d[curVertex] + nxt.cost;
                    pq.offer(new Pair(d[nxt.vertex], nxt.vertex));
                }
            }
        }

        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        for (int i = 1; i <= v; i++) {
            if (d[i] == INF) {
                bw.write("INF\n");
            } else {
                bw.write(d[i] + "\n");
            }
        }
        bw.flush();
        bw.close();
    }
}

class Pair {
    int cost, vertex;

    Pair(int cost, int vertex) {
        this.cost = cost;
        this.vertex = vertex;
    }
}