[알고리즘] 유클리드 호제법

프로그래머스 문제를 풀던 중 최대공약수 관련 문제를 풀 때마다 유클리드 알고리즘을 까먹어 복기하고자 기록한다.

최대 공약수(GCD, Greatest Common Divisor)

최대 공약수는 두 자연수의 공통된 약수 중 가장 큰 수를 말한다.

기존에 최대공약수를 구하려면 두 수 중 작은 수부터 1까지 작은 수까지 모든 수를 비교해가며 동시에 나누어 떨어지는 가장 큰 수를 구해야 했다.

def gcd(a, b): # 큰수: a, 작은수: b
    for i in range(b, 0, -1):
    	if a % i == 0 and b % i == 0:
        	return i

위의 코드의 경우 시간복잡도는 O(N) 이다.

유클리드 알고리즘

유클리드 호제법은 최대공약수를 구하는 알고리즘이다. 유클리드 알고리즘을 사용하면 시간복잡도를 O(logN)으로 단축할 수 있다.

유클리드 호제법에 대해 더 알아보자

정의

2개의 자연수 a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다

위의 정의에 따라 공식을 세우면 아래와 같은 공식이 나온다.

gcd(a, b) = gcd(b, a % b)

우리는 위의 공식을 활용하여 1980, 168 의 최대공약수를 구한다고 하자.

gcd(1980, 168) = gcd(168, 132)
gcd(168, 132) = gcd(132, 36)
gcd(132, 36) = gcd(36, 24)
gcd(36, 24) = gcd(24, 12)

24를 12로 나누었을 때 나머지는 0이라는 것을 알 수 있다.
따라서 유클리드 알고리즘은 a를 b로 나눈 나머지가 0이 나왔을 때 b의 값이 최대공약수이다.

재귀함수로 작성한 코드

def gcd(a, b): # 큰수: a, 작은수: b
	if b == 0:
    	return a
    return gcd(b, a % b)

앞서 살펴본 유클리드 알고리즘 정의로 작성한 코드이다. 나머지(b)가 0인경우 최대공약수(a)를 반환한다.

최소 공배수(LCM, Least Common Multiple)

최소 공배수는 두 수의 배수 중에서 공통된 가장 작은 수를 말한다.

최소 공배수를 구하는 방법은 간단하다. 두 수를 곱한 값에서 최대공약수로 나누면 최소공배수가 나온다.

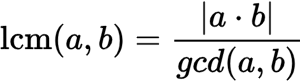
앞서 보았던 1980과 168의 최대공약수 12를 이용해 쉽게 최소 공배수를 구할 수 있다.

lcm(1980, 168) = (1980 * 168) / 12 = 27720

코드

def lcm(a, b):
    return a * b // gcd(a, b)

📕 참고 문헌

다음의 링크를 참고했습니다.
위키백과 유클리드 호제법
[알고리즘] 최소공배수, 최대공약수와 유클리드 알고리즘