기술적지표2 - MACD(이동평균수렴·확산지수)

이동평균

이동평균이란 이동하는 가격의 적정한 평균치를 수학적으로 산출하는것이다. 다양한 방법이 있으며, 이를 통해 추세의 범위와 이탈 등을 확인하는 용도로 쓰인다. 가장 대표적으로 사용되는 이동평균기법은 SMA와 EMA가 있다.

SMA(단순이동평균)

단순이동평균은 가장 기본적인 이동평균 계산 방법으로 과거 일정 일수 동안의 가격을 더하여 해당 일수로 나누어 계산한다.

SMA(N) = 직전 N일간의 평균 가격 = 직전 N일간의 가격 합계 / N

단순이동평균선을 20일과 5일로 그려보자.

import matplotlib.pyplot as plt
import mplfinance as mpf
import numpy as np

df['SMA20'] = df['close'].rolling(20).mean()
df['SMA5'] = df['close'].rolling(5).mean()

df_draw = df[-200:]

adps = []
adps.append(
   mpf.make_addplot(df_draw['SMA20'],panel=0,type='line'))
adps.append(
   mpf.make_addplot(df_draw['SMA5'],panel=0,type='line'))


fig, axs = mpf.plot(df_draw, style='charles', figratio=(3,2),figscale=1.5, addplot=adps, returnfig=True)

axs[0].legend(['SMA20', 'SMA5'])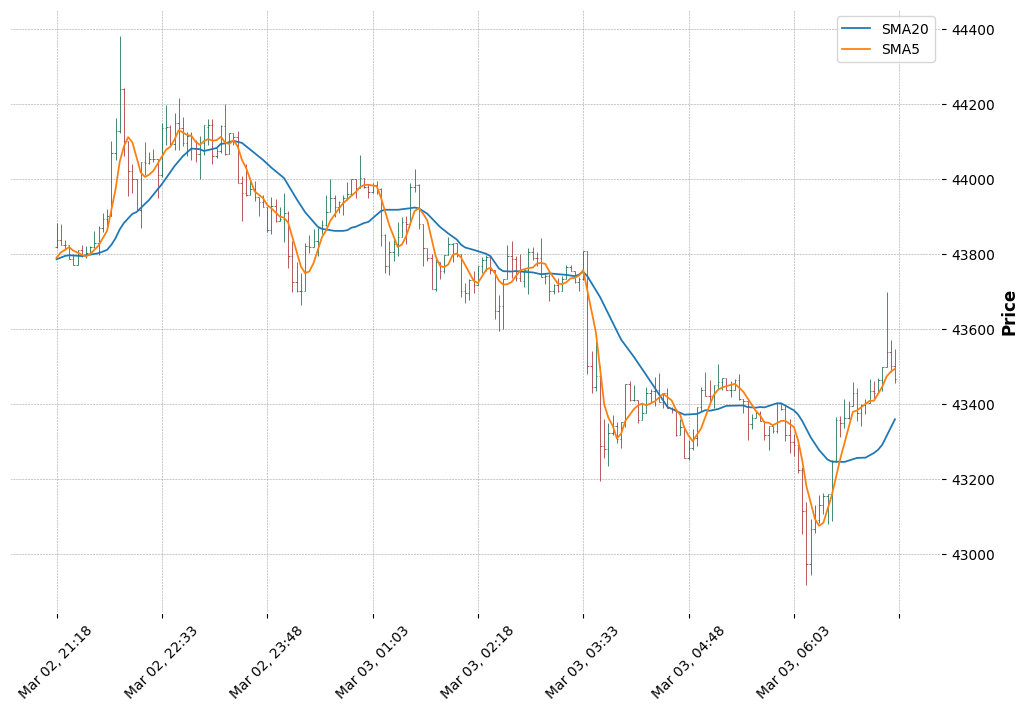

EMA(지수이동평균)

SMA와 다르게 EMA는 최근 가격에 가중치를 두어 이동평균을 계산하는 방법이다.

EMA = $(가격 \ \alpha) + (전일의 EMA * (1 - \alpha))$
$\alpha$ = 2 / (기간 + 1)

식을 생각해보면 EP는 기간이 길어질수록 작은 값을 가진다. 또한 EMA값은 이전의 EMA에 EP비율만큼 현재값을 반영하게 되니 최근으로 올수록 점점 평균값을 낼때 가중치를 많이 두게 된다. 식 자체를 이해할 필요는 없다. 다만 최근 추이를 좀더 반영한다 정도로 이해하고 아래와 같이 쉽게 코딩으로 나타낼 수 있다.

지수이동평균선을 20일과 5일로 그려보자.

import matplotlib.pyplot as plt
import mplfinance as mpf
import numpy as np

df['EMA20'] = df['close'].ewm(20, adjust=False).mean()
df['EMA5'] = df['close'].ewm(5, adjust=False).mean()

df_draw = df[-200:]

adps = []
adps.append(
   mpf.make_addplot(df_draw['EMA20'],panel=0,type='line'))
adps.append(
   mpf.make_addplot(df_draw['EMA5'],panel=0,type='line'))


fig, axs = mpf.plot(df_draw, style='charles', figratio=(3,2),figscale=1.2, addplot=adps, returnfig=True)

axs[0].legend(['EMA20', 'EMA5'])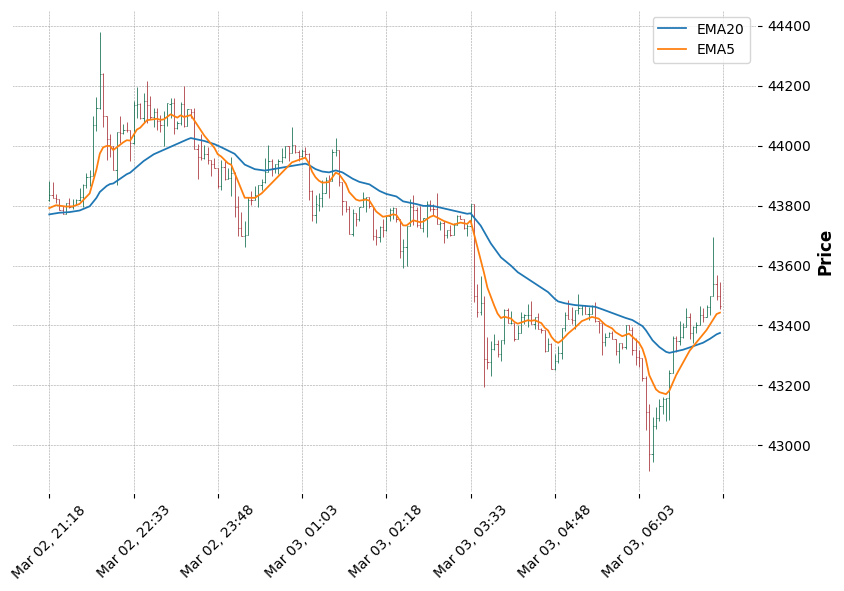

SMA와 5일선을 비교하면 조금더 실제 최근가격에 붙어서 움직이는 느낌을 받을 수 있다.

MACD(이동평균수렴·확산지수)

MACD란?

이동평균수렴·확산지수는 추세의 강도를 측정한다. 가격의 방향을 나타내는 다른 지표와는 달리, MACD는 추세 모멘텀의 방향을 보여준다.

MACD(12, 26) = EMA12 - EMA26

일반적으로는 아래와 같이 MACD를 설명한다.

• MACD가 증가하면 상승국면
• 음수에서 양수로 바뀌면서 올라갈때 추세가 전환되었다고 평가

단기지수평균 - 장기지수평균에 대해서 생각해보자. MACD가 0이란말은 장기 텀의 가격과 단기 텀의 가격이 같아졌음을 의미한다. 또한 양의값을 가진다는것은 단기 평균이 장기 평균보다 높다는말이고 이는 곧 최근 가격 추이가 과거보다 높아진곳에서 형성된것을 의미한다.

import matplotlib.pyplot as plt
import mplfinance as mpf
import numpy as np

df['EMA12'] = df['close'].ewm(12, adjust=False).mean()
df['EMA26'] = df['close'].ewm(26, adjust=False).mean()

df['MACD'] = df['EMA12'] - df['EMA26']

df_draw = df[-500:]

adps = []
adps.append(
    mpf.make_addplot(df_draw['EMA12'],panel=0,type='line'))
adps.append(
    mpf.make_addplot(df_draw['EMA26'],panel=0,type='line'))
adps.append(
    mpf.make_addplot(df_draw['MACD'],panel=1,type='line', ylabel='MACD'))
adps.append(
    mpf.make_addplot(np.zeros((len(df_draw))), panel=1,type='line', color='red', linestyle='dotted',secondary_y=False))


fig, axs = mpf.plot(df_draw, style='charles', figratio=(4,3),figscale=1.5, addplot=adps, returnfig=True)

axs[0].legend(['EMA12', 'EMA26'])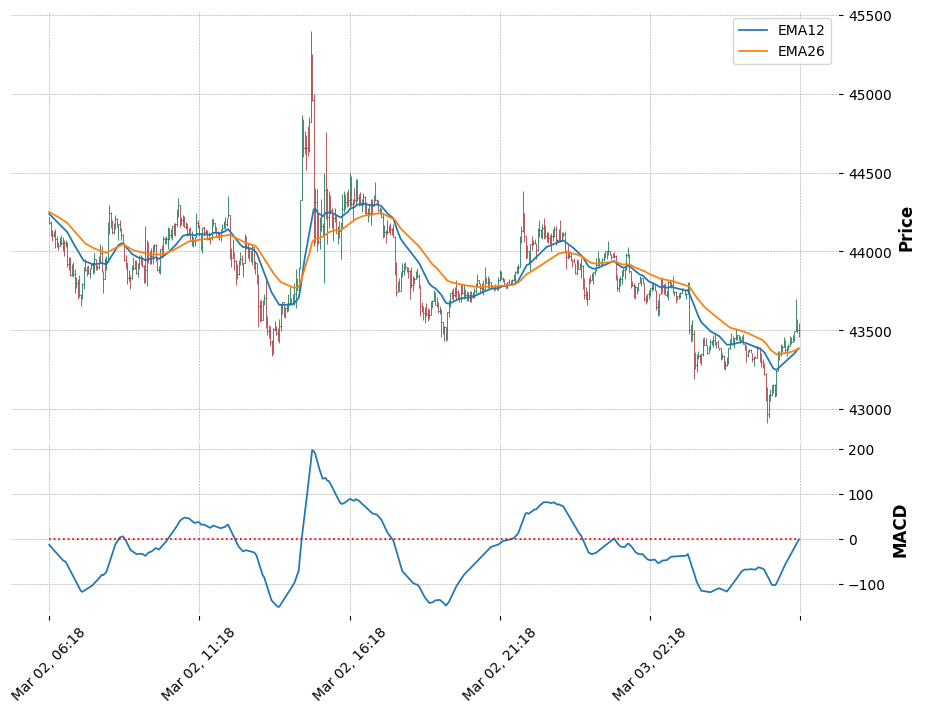

MACD Signal

MACD Signal(9) = MACD의 9일 단순이동평균선

MACD(12, 26, 9) 에서 MACD는 위와 같이 구할수 있고 해당 MACD의 9일 지수이동평균선으로 MACD Signal을 구할 수 있다.

import matplotlib.pyplot as plt
import mplfinance as mpf
import numpy as np

df['EMA12'] = df['close'].ewm(12, adjust=False).mean()
df['EMA26'] = df['close'].ewm(26, adjust=False).mean()

df['MACD'] = df['EMA12'] - df['EMA26']

df['MACD_Signal'] = df['MACD'].ewm(9, adjust=False).mean()

df_draw = df[-500:]

adps = []
adps.append(
    mpf.make_addplot(df_draw['EMA12'],panel=0,type='line'))
adps.append(
    mpf.make_addplot(df_draw['EMA26'],panel=0,type='line'))
adps.append(
    mpf.make_addplot(df_draw['MACD'],panel=1,type='line', ylabel='MACD'))
adps.append(
    mpf.make_addplot(df_draw['MACD_Signal'],panel=1,type='line', color='orange',secondary_y=False))
adps.append(
    mpf.make_addplot(np.zeros((len(df_draw))), panel=1,type='line', color='red', linestyle='dotted',secondary_y=False))


fig, axs = mpf.plot(df_draw, style='charles', figratio=(4,3),figscale=1.5, addplot=adps, returnfig=True)

axs[0].legend(['EMA12', 'EMA26'])
axs[2].legend(['MACD', 'MACD_SIGNAL'])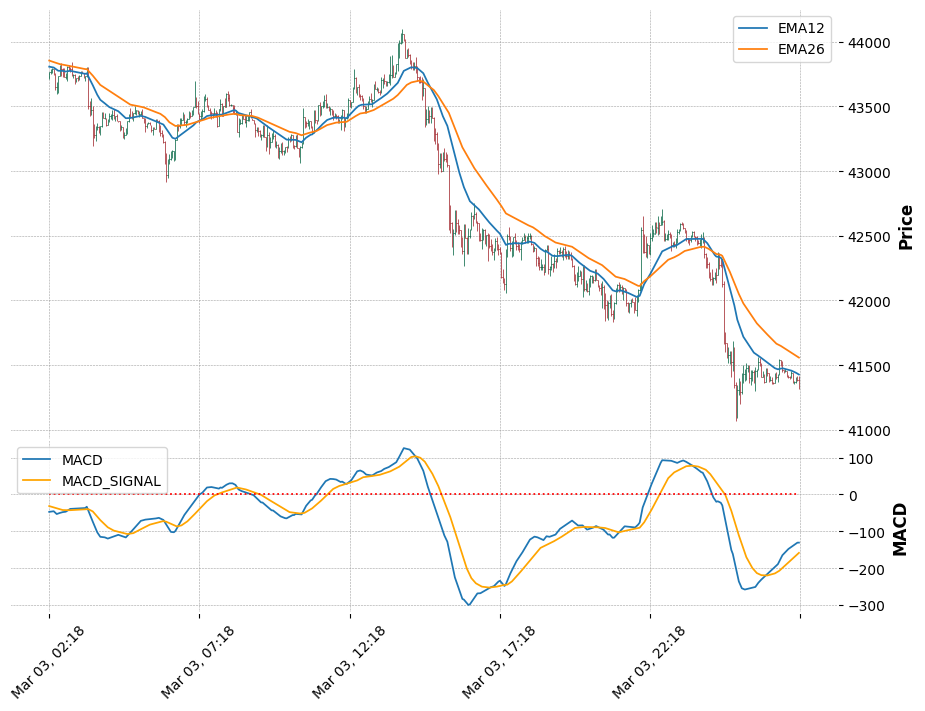

MACD Signal을 활용하여 의미를 풀어보면 일반적으로

• MACD가 증가하면 상승국면, 특히 0보다 작았다가 양수로 변할때 추세가 전환되었다고 생각 할 수 있다.
• MACD가 Signal을 상향돌파하면 상승신호, 하향돌파하면 하락 신호라 생각 할 수 있다.

물론 위와같은 정설대로 거래해서는 이제 수익을 창출하기 힘들다. 다 알려진 전략은 많은사람들이 해당 방법으로 차익을 얻어가는 순간
패턴이 깨지기 때문이다.(매수, 매도로 인해 차트의 패턴이 변화되게 된다.) 그러나, 이러한 변화로 인해 또다른 패턴이 만들어지고, 그 패턴으로 또 돈을 버는 사람들이 생긴다. 즉, 사견이지만 이 세상에 영원히 수익을 버는 마법공식 전략은 존재하지 않는다. 또한, 항상 그 시점에서 수익을 버는 전략(패턴)은 존재한다.

MACD와 MACD Signal을 활용한 투자 전략

MACD Signal의 상향돌파와 하향돌파가 직관적으로 위 선그래프로는 잘 보이지 않기에 두개의 차이를 막대그래프로 오실레이터에 나타내어 보자.

import matplotlib.pyplot as plt
import mplfinance as mpf
import numpy as np

df['EMA12'] = df['close'].ewm(12, adjust=False).mean()
df['EMA26'] = df['close'].ewm(26, adjust=False).mean()

df['MACD'] = df['EMA12'] - df['EMA26']

df['MACD_Signal'] = df['MACD'].ewm(9, adjust=False).mean()
df['MACD_OSC'] = df['MACD'] - df['MACD_Signal']

df_draw = df[-500:]

adps = []
adps.append(
    mpf.make_addplot(df_draw['EMA12'],panel=0,type='line'))
adps.append(
    mpf.make_addplot(df_draw['EMA26'],panel=0,type='line'))
adps.append(
    mpf.make_addplot(df_draw['MACD'],panel=1,type='line', ylabel='MACD'))
adps.append(
    mpf.make_addplot(df_draw['MACD_Signal'],panel=1,type='line', color='orange',secondary_y=False))
adps.append(
    mpf.make_addplot(np.zeros((len(df_draw))), panel=1,type='line', color='red', linestyle='dotted',secondary_y=False))
adps.append(
    mpf.make_addplot(df_draw['MACD_OSC'],panel=1,type='bar', color='green',secondary_y=False))


fig, axs = mpf.plot(df_draw, style='charles', figratio=(4,3),figscale=1.5, addplot=adps, returnfig=True)

axs[0].legend(['EMA12', 'EMA26'])
axs[2].legend(['MACD', 'MACD_SIGNAL'])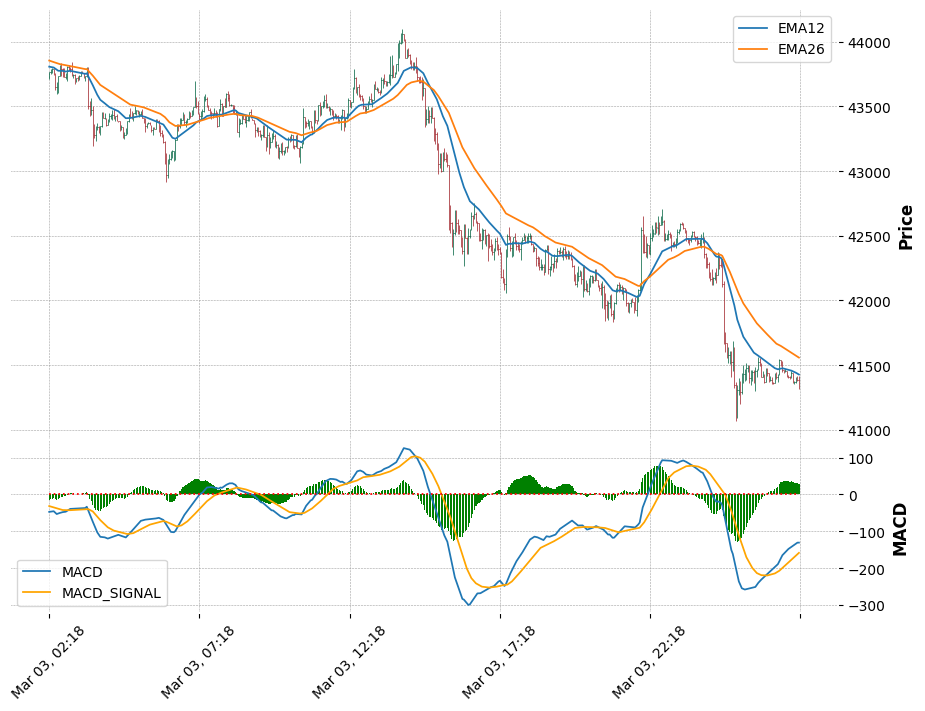

이제 각 지표들이 어떤의미를 가지고 있고, 이를 활용해서 어떻게 거래해야 창기을 만들어낼 수 있을지 본인만의 전략을 생각해보길 바란다.