
🌈 Hash Tables
Hash Tables 이란?
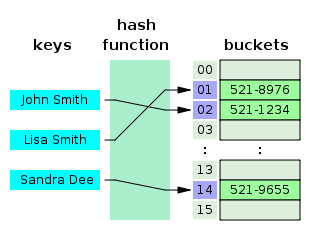
- 해시 테이블은 (Key, Value)로 데이터를 저장하는 자료구조 중 하나이다.
- 각각의 Key 값에 해시함수를 적용해 고유 index를 생성하고, 이 값을 활용해 Value 값을 저장 or 검색 한다.
- 해시 테이블은 빠르게 데이터를 검색할 수 있는 자료구조인데, 빠른 검색속도를 제공하는 이유는 내부적으로 배열(버킷)을 사용하여 데이터를 저장하기 때문이다.
- 실제 값이 저장되는 장소를 버킷(bucket) 또는 슬롯(slot)이라고 한다. 해시 테이블은 해시 함수를 사용하여 index를 버킷이나 슬롯의 배열로 계산한다.
Hash Tables의 장단점
👉 장점
- 해싱된 키(Hash Key)를 가지고 배열의 인덱스로 사용하기 때문에 삽입, 삭제, 검색이 매우 빠르다.
- 해시 충돌이 발생할 가능성이 있음에도 해시 테이블이 많이 쓰이는 이유는 적은 리소스로 많은 데이터를 효율적으로 관리할 수 있기 때문이다.
👉 단점
- 순서가 있는 배열(연속적인 배열)에는 적합하지 않다.
- Collision(충돌)이 일어날 경우 해시 테이블의 성능에 지대한 영향을 끼친다. 충돌이 없거나 적으면 O(1)의 상수 시간에 가까워지고, 충돌이 발생하면 할수록 성능은 점점 O(n)에 가까워진다.
- 적은 데이터 저장시 구현 방식에 따라 연결리스트(Linked List)를 사용하는 경우 오버 헤드의 부담이 생기고, 캐시 효율이 떨어진다.
해싱(Hashing) 이란?
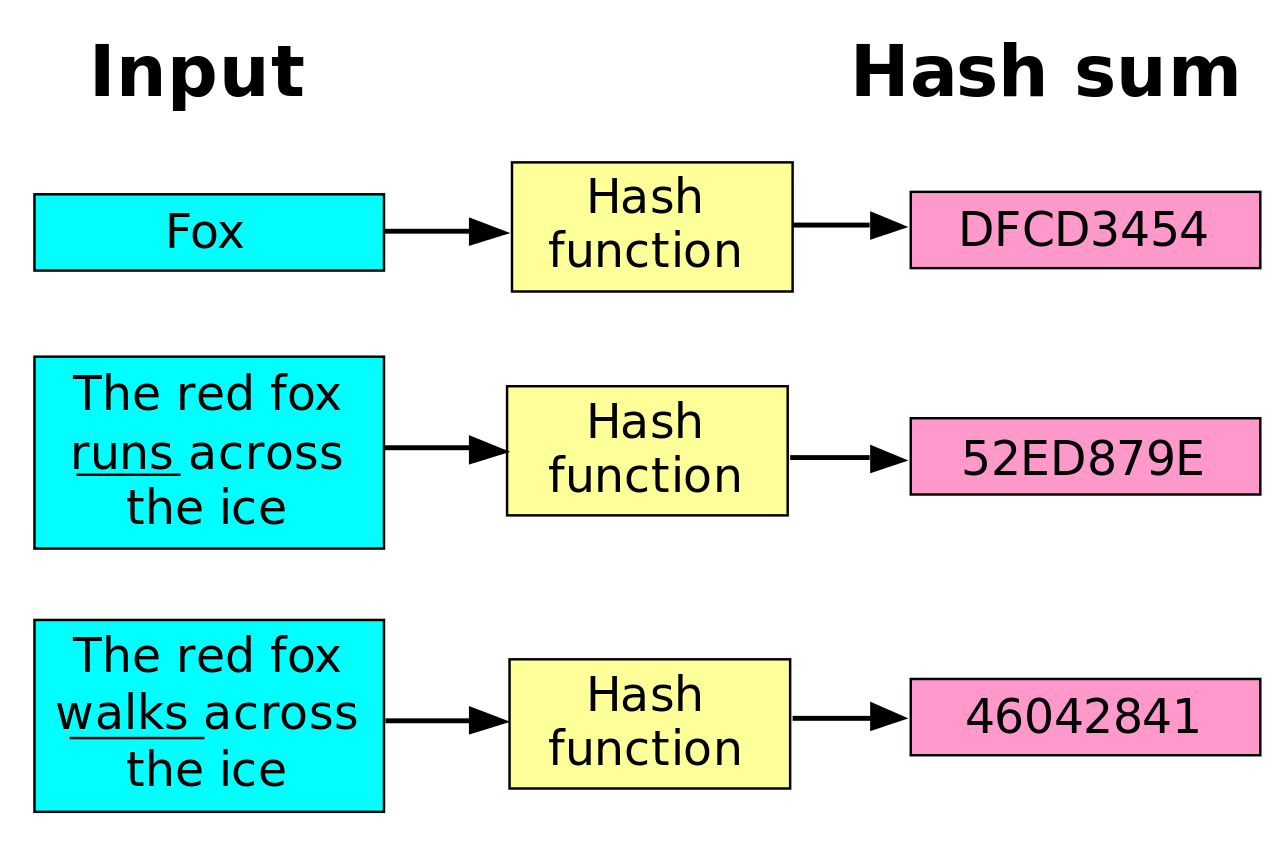
- 해싱은 가변 크기의 입력값에서 고정된 크기의 출력값을 생성해 내는 과정을 의미한다. 이는 해시 함수(해싱 알고리즘으로 구현됨)라 알려진 수학적 공식을 따라 진행된다.
해시테이블(HashTable) 시간복잡도
-
각각의 Key값은 해시함수에 의해 고유한 index를 가지게 되어 바로 접근할 수 있으므로 평균 O(1)의 시간복잡도로 데이터를 조회할 수 있다(삽입/탐색/삭제 모두 O(1)). 하지만 이는 어디까지나 데이터의 충돌이 발생하지 않았을 경우의 얘기이다.
-
데이터의 충돌이 발생한 경우 Chaining에 연결된 리스트들까지 검색을 해야 하므로 O(N)까지 시간복잡도가 증가할 수 있다.
-
충돌을 방지하는 방법들은 데이터의 규칙성(클러스터링)을 방지하기 위한 방식이지만 공간을 많이 사용한다는 치명적인 단점이 있다.
-
해시 테이블에서 자주 사용하게 되는 데이터를 Cache에 적용하면 효율을 높일 수 있다. 자주 hit하게 되는 데이터를 캐시에서 바로 찾음으로써 해시 테이블의 성능을 향상시킬 수 있다.
Hash Function
- 해시 함수는 임의의 길이를 갖는 임의의 데이터에 대해 고정된 길이의 데이터로 매핑하는 함수이다.
간단한 용어 정리를 해보면 아래와 같다.
✔ 매핑 후 데이터의 값을 해시 값(hash value)
✔ 해시 값 + 데이터의 index 주소를 해시 테이블(Hash table)
✔ 매핑하는 과정 자체를 해싱(hashing)
-
해시 함수에서 중요한 것은 고유한 인덱스 값을 설정하는 것이다. 해시 테이블에 사용되는 대표적인 해시 함수로는 아래와 같은 종류가 있다.
-
Division Method: 나눗셈을 이용하는 방법으로 입력값을 테이블의 크기로 나누어 계산한다.( 주소 = 입력값 % 테이블의 크기) 테이블의 크기를 소수로 정하고 2의 제곱수와 먼 값을 사용해야 효과가 좋다고 알려져 있다.
-
Digit Folding: 각 Key의 문자열을 ASCII 코드로 바꾸고 값을 합한 데이터를 테이블 내의 주소로 사용하는 방법이다.
-
Multiplication Method: 숫자로 된 Key값 K와 0과 1사이의 실수 A, 보통 2의 제곱수인 m을 사용하여 다음과 같은 계산을 해준다. h(k)=(kAmod1) × m
-
Univeral Hashing: 다수의 해시함수를 만들어 집합 H에 넣어두고, 무작위로 해시함수를 선택해 해시값을 만드는 기법이다.
-
간단한 Hash Table 구현
# hash table(empty)
hash_table = list([0 for i in range(8)])
# 해시 함수 (Division 방식: 나머지 값 사용)
def hash_func(key):
return key % 8
def save_data(data, value):
key = ord(data[0])
hashed_key = hash_func(key)
hash_table[hashed_key] = value
save_data('Chankyu', 'lck0827@gmail.com')
save_data('Tom', 'tom@gmail.com')
save_data('James', 'James@gmail.com')
print(hash_table)ord()문자의 유니코드를 반환하는 함수이다.chr()함수와 반대!
Hash Collisions
해시 테이블에서는 충돌에 의한 문제의 해결책으로 Open Hahsing(Chaining)과 Close Hashing의 2가지를 자주 사용한다.
👉 Open Hashing (Chaining)
-
한 버킷당 들어갈 수 있는 엔트리의 수에 제한을 두지 않는 방법
-
이미 데이터가 존재하는 버킷에 데이터를 추가해야 할 경우 체인처럼 노드를 추가하여 다음 노드를 가리키는 방식으로 구현
-
연결 리스트(Linked List)를 이용한 방식으로 각 index에 데이터를 저장하는 Linked list에 대한 포인터를 가지는 방식이다.
-
메모리 문제를 야기할 수 있다는 단점이 있다.
-
검색은 해시 함수(Hash Function)을 통해 인덱스를 구하고 해당 인덱스의 연결 리스트(Linked List)를 선형적으로 검사하여 해당 키(Key)의 노드(Node)가 존재하는지 확인하고 값(Value)를 리턴한다.
-
삭제는 검색과 동일하게 해당 인덱스의 연결 리스트(Linked List)를 선형적으로 검사하여 해당 키(Key)의 노드(Node)를 삭제하면 된다.
-
연결 리스트(Linked List)를 이용하기 때문에 추가할 수 있는 데이터의 제약이 적다.
-
해시 함수(Hash Function) 구현(선택)하는 관점에서, Chaining Hash Table의 경우 클러스터링(Clustering)에 거의 영향을 받지 않아 충돌의 최소화만 중점적으로 고려하면 된다.
-
해시 테이블의 버킷(Bucket)이 채워져도 성능 저하가 선형적으로 발생한다.
-
테이블의 높은 부하율(Load Factor)가 예상되거나, 데이터가 크거나, 데이터의 길이가 가변일 때 성능이 좋아진다.
# 개방 주소법
hash_table = list([0 for i in range(10)])
def get_key(data): #해쉬 키 생성
return hash(data)
def hash_func(key):
return key % 8
def save_data(data, value):
index_key = get_key(data)
hash_address = hash_func(index_key)
# 해쉬 충돌이 발생할 경우(해쉬 주소가 동일할 경우)
if hash_table[hash_address] != 0:
for index in range(len(hash_table[hash_address])):
# Key가 동일하면 데이터를 덮어씀
if hash_table[hash_address][index][0] == index_key:
hash_table[hash_address][index][1] == value
return
# Key가 동일하지 않으면 데이터를 연결해 저장함
hash_table[hash_address].append([index_key, value])
# 2. 해쉬 충돌이 발생하지 않으면 해당 버킷에 데이터 저장
else:
hash_table[hash_address] = [[index_key, value]]
# 데이터 조회
def read_data(data):
index_key = get_key(data)
hash_address = hash_func(index_key)
if hash_table[hash_address] != 0:
for index in range(len(hash_table[hash_address])):
if hash_table[hash_address][index][0] == index_key:
return hash_table[hash_address][index][1]
return None
else:
return None
save_data('Chankyu', 'lck0827@gmail.com')
save_data('Tom', 'Tom@gmail.com')
save_data('James', 'James@gmail.com')
print(hash_table)
# [0, [[8053009201448131705, 'Tom@gmail.com']], [[-4393140602619313294, 'James@gmail.com']], 0, 0, 0, [[7053794814996265366, 'lck0827@gmail.com']], 0, 0, 0]
print(read_data('Chankyu')) # lck0827@gmail.com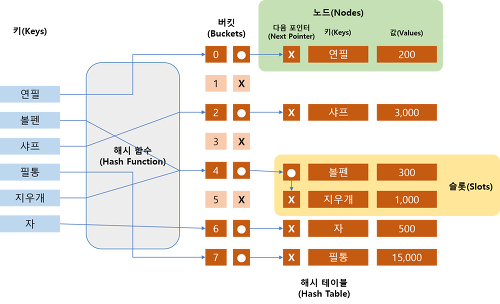
👉 Close Hashing 기법
-
분리 연결법과는 다르게 한 버킷당 들어갈 수 있는 엔트리는 하나 뿐이다.
-
hash table array의 빈공간을 사용하는 방법이기 때문에 Linked list와 같은 추가적인 메모리 공간 사용은 없다.
-
충돌이 발생하면 다른 버킷(Bucket)에 저장하기 때문에 데이터의 주소 값(index)이 바뀐다.
-
포인터(Pointer)를 사용하지 않음으로써 직렬화(Serialization)가 용이하다.
-
개방 주소법은 삭제가 어렵다는 단점이 있다. 삭제 했을 경우 충돌에 의해서 뒤로 저장된 데이터가 검색이 안될 수 있다. 이를 방지하기 위해 삭제한 위치에 Dummy Node를 삽입한다. Dummy Node는 실제 값을 가지지는 않지만, 검색할 때 다음 위치(인덱스)까지 연결해주는 역할을 한다. 하지만 삭제가 빈번히 일어날 경우 Dummy Node 수가 많아져서 검색할 경우에 많은 버킷(Bucket)을 연속적으로 검색해야 하기 때문에 이 Dummy Node의 개수가 일정 수 이상이 되었을 경우에 주기적으로 새로운 배열을 만들어고 재해시(Rehash)를 해줘야 성능을 유지할 수 있다.
-
개방 주소법의 여러 구현 방식 중 간단한 선형 검색법에 대해 알아보겠다.
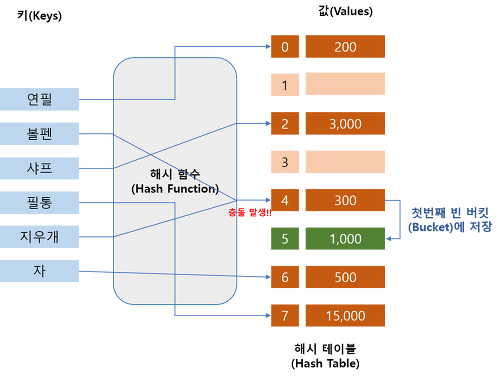
👉 선형 검색법(Linear Probing)
-
index에 의해 충돌이 발생했을 때, 충돌이 일어난 위치에서 선형적으로 검색하여 뒤에있는 버킷 중에 첫 번째 빈 버킷을 찾아서 데이터를 저장하는 방식이다.
-
테이블의 끝에 도달하게 되면 처음으로 되돌아 간다.
-
조사를 시작한 위치로 되돌아 오게 되면 테이블이 가득찬 것이다.
-
-
장점 : 구조가 간단하고 캐시의 효율이 높다.
-
단점 : 최악의 경우 해시 테이블(Hash Table) 전체를 검색해야 하는 상황이 발생할 수 있으므로 비효율적이고, 데이터의 클러스터링(Clustering)에 가장 취약하다.
-
hash_table = list([0 for i in range(10)]) # 빈 해쉬 테이블 생성
def get_key(data): # 해쉬 키 생성
return hash(data)
def hash_func(key): # 간단한 해쉬 함수
return key % 8
def save_data(data, value):
index_key = get_key(data)
hash_address = hash_func(index_key)
# 해쉬 충돌이 발생할 경우(해쉬 주소가 동일한 경우)
if hash_table[hash_address] != 0:
# 충돌 일어난 위치부터 끝까지 스캔
for index in range(hash_address, len(hash_table)):
# 동일한 key 일 경우 덮어쓰기
if hash_table[index] == 0:
hash_table[index] = [index_key, value]
return
# 빈 공간 찾으면 저장
elif hash_table[index][0] == index_key:
hash_table[index][1] = value
# 충돌 없으면 데이터 바로 저장
else:
hash_table[hash_address] = [index_key, value]
# 해쉬 데이터 조회
def read_data(data):
index_key = get_key(data)
hash_address = hash_func(index_key)
if hash_table[hash_address] != 0:
for index in range(hash_address, len(hash_table)):
if hash_table[index] == 0:
return None
elif hash_table[index][0] == index_key:
return hash_table[index][1]
else:
return None
save_data('Chankyu', 'lck0827@gmail.com')
save_data('Tom', 'Tom@gmail.com')
save_data('James', 'James@gmail.com')
print(hash_table)
#[0, [2266316231113885169, 'James@gmail.com'], 0, [-7075593178918954781, 'Tom@gmail.com'], 0, 0, 0, [9217761794924333335, 'lck0827@gmail.com'], 0, 0]
print(read_data('Chankyu')) # lck0827@gmail.comAppendix
해시 알고리즘
- 대표적인 해시 알고리즘으로는 Message-Digest Algorithm(MD)과 Secure Hash Algorithm(SHA) 등이 있다.
- MD5
- 임의의 길이의 값을 입력 받아서 128비트 길이의 해시값을 출력한다.
- 단방향 암호화이기 때문에 출력값 -> 입력값 복원은 할 수 없다.
- 같은 입력값이면 항상 같은 출력값이 출력되며, 서로 다른 입력값에서 같은 출력값이 나올 확률은 매우 낮다.
- 현재는 MD5 알고리즘을 보안 관련 용도로 쓰는 것을 권장하지 않는다.
- SHA
- 팀 프로젝트 진행하며 bcrpyt 암호화시 사용했던 SHA256 알고리즘의 SHA이다. 현업에서 많이 사용되고 있는 패스워드 암호화 알고리즘이다.
- 미국 국립표준기술연구소(NIST)에서 표준으로 채택한 암호학적 해시 함수이다.
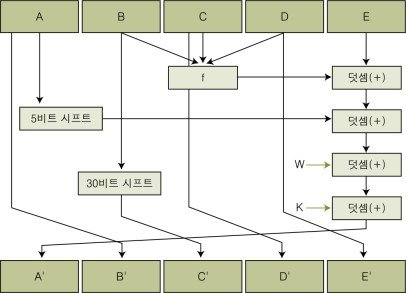
- SHA에 입력하는 데이터는 512비트의 블록이고, 160비트의 값을 생성하는 해시 함수로서 MD4가 발전한 형태이다.
- 알고리즘의 동작원리는 아래 그림과 같다.
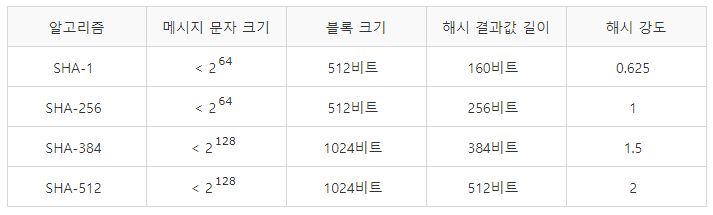
- 종류에 따른 성능은 아래의 표를 참고
해시의 사용 예시
- 비밀번호 저장
- 프로젝트를 진행하며 이미 직접 해본적이 있는 예시이다. 클라이언트의 ID와 Password가 입력되면 DB의 users table에 ID와 해싱된 Password값을 저장한다.
-
복제문서 판별
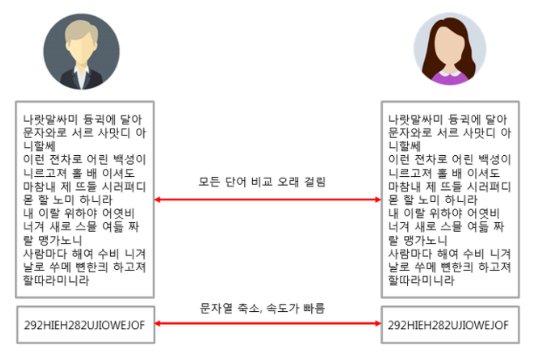
-
검색
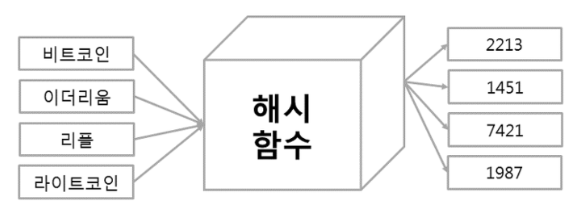
Reference
1. https://mangkyu.tistory.com/102
2. https://dev-kani.tistory.com/1
3. https://yjshin.tistory.com/entry/%EC%95%94%ED%98%B8%ED%95%99-%ED%95%B4%EC%8B%9C-%ED%95%A8%EC%88%98-%EC%9E%91%EC%84%B1-%EC%A4%91
4. https://steemit.com/kr/@yahweh87/2