TIL-076 | 그래프 탐색(2)-BFS

🌈 그래프 탐색(2) - BFS

너비 우선 탐색(Breadth-First Search, BFS)란?

• BFS는 DFS와 함께 그래프 전체를 탐색하는 방법 중 하나이다.
• 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색한다. 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하여 순회함으로써 노드를 넓게(wide) 탐색한다.
• 너비 우선 탐색은 최단 경로를 찾아주기에 최단 길이를 보장해야할 때 많이 사용한다.
• 구현할 때 큐라는 자료에 이웃하는 정점을 다 담아놓고 차례대로 POP을 하는 방식으로 구현한다.

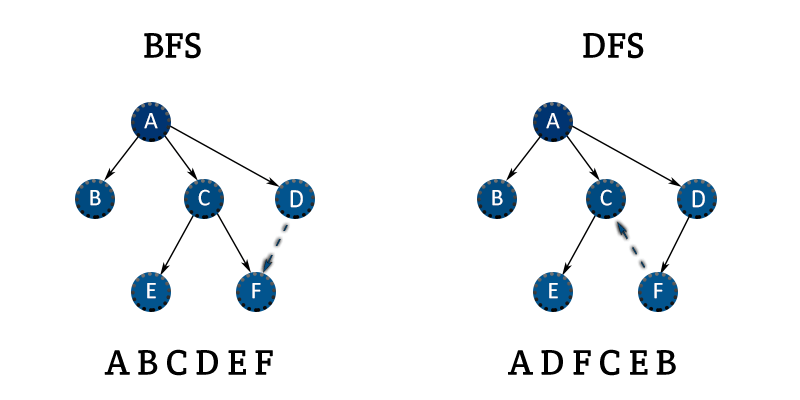
BFS의 특징

• 직관적이지 않은 면이 있다.
  • BFS는 시작 노드에서 시작해서 거리에 따라 단계별로 탐색한다고 볼 수 있다.
• DFS와 다르기 BFS는 재귀적으로 동작하지 않는다.
• 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다. 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
• BFS는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용한다.
  • 선입선출(FIFO) 원칙으로 탐색
  • 일반적으로 큐를 이용해서 반복적 형태로 구현하는 것이 가장 잘 동작한다.
• ‘Prim’, ‘Dijkstra’ 알고리즘과 유사함.

BFS의 장점

• 노드의 수가 적고 깊이가 얕은 경우 빠르게 동작할 수 있다.
• 단순 검색 속도가 깊이 우선 탐색(DFS)보다 빠름
• 너비를 우선 탐색하기에 답이 되는 경로가 여러개인 경우에도 최단경로임을 보장한다.
• 최단경로가 존재한다면 어느 한 경로가 무한히 깊어진다해도 최단경로를 반드시 찾을 수 있다.

BFS의 단점

• 재귀호출의 DFS와는 달리 큐에 다음에 탐색할 정점들을 저장해야 하므로 저장공간이 많이 필요하다.
• 노드의 수가 늘어나면 탐색해야하는 노드 또한 많아지기에 비현실적이다.

BFS의 시간복잡도

• 인접 리스트로 표현된 그래프: 노트(N) 개수 + 간선(E) 개수 = O(N+E)
• 인접 행렬로 표현된 그래프: O(N^2)
• 깊이 우선 탐색(DFS)과 마찬가지로 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다.

BFS의 구현

• 자료 구조 큐(Queue)를 이용한다.

graph_list = {1: set([3, 4]),
              2: set([3, 4, 5]),
              3: set([1, 5]),
              4: set([1]),
              5: set([2, 6]),
              6: set([3, 5])}
root_node = 1

• 위와 같이 방향이 있는 유향 그래프를 BFS로 탐색하면 아래와 같이 구현한다.

from collections import deque

def BFS_with_adj_list(graph, root):
    visited = []
    queue = deque([root])

    while queue:
        n = queue.popleft()
        if n not in visited:
            visited.append(n)
            queue += graph[n] - set(visited)
    return visited
  
print(BFS_with_adj_list(graph_list, root_node))

📝 Reference

1. https://coding-factory.tistory.com/612
2. https://blog.naver.com/ndb796/221230944971
3. https://gmlwjd9405.github.io/2018/08/15/algorithm-bfs.html