[컴퓨터비전 STUDY / KOCW 한동대학교 황성수 교수님 강의 Review]
Introduction
카메라는 3D 장면 공간과 2D 영상 평면 사이의 매핑을 위한 장비이다.
이미지 처리 분야에서 이미지의 기하학적 해석은 대부분 핀홀 카메라 모델을 기반으로 한다.
<예비 조건>
-
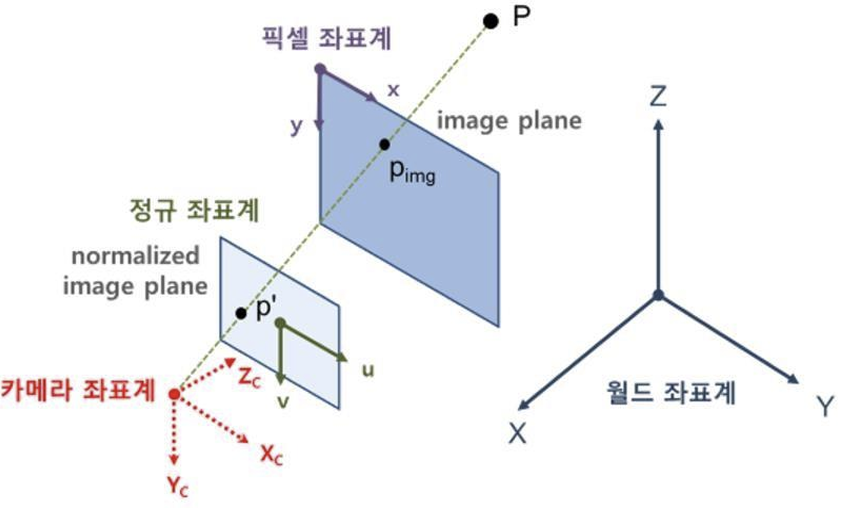
World coordinate (3D) : 물체의 위치를 표현할 때 기준으로 사용되는 좌표계로 원점을 (0,0,0)으로 지정한다.
-
Camera coordinate (3D) : 카메라 원점에 대한 좌표계
-
Normalized image plane : 카메라의 고유 파라미터의 영향을 제거하고, 초점거리가 1인 가상 이미지 평면을 정의하는 이미지를 위한 좌표계
-
Pixel coordinate (=image plane, 2D) : 영상의 좌표계
그림으로 표현하면 다음과 같다.
[비균질 좌표]
2D point -> (x, y)
3D point -> (x, y, z)
[균질 좌표]
2D point -> (x, y, 1)
3D point -> (x, y, z, 1)
(x, y, z, 1) = (2x, 2y, 2z, 2) <- 규모에 필적함
Camera Model
3차원점 X가 존재할 때, x점으로 투영되는데 그 점에 대응되는 x의 좌표가 무엇일까?
-
camera center가 world coordinate의 원점에 있다고 가정
-
camera center 원점에서 수직으로 그은 Z축이 image plane과 만나는 점은 principal point라고 함
-
따라서 image plane 위에 있는 좌표는 (0, 0, f)가 된다.
f는 principal plane과 image plane의 거리이다.
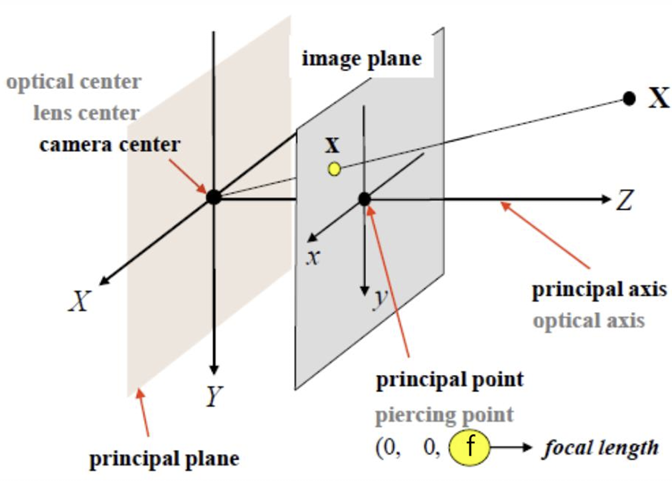
3차원 점이 2차원 점으로 투영됨 (X와 x의 관계)
삼각형 닮음 관계로 밑의 식이 성립하는 것도 알 수 있다.
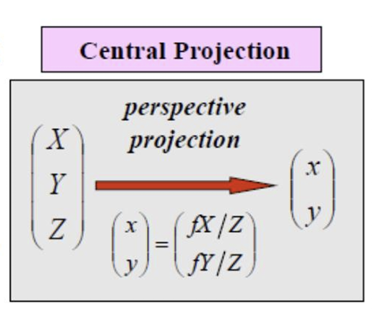
Homogeneous coordinat를 사용해서도 표현할 수 있다.
예를 들어, 밑의 그림에서 kX * f = wx이다.
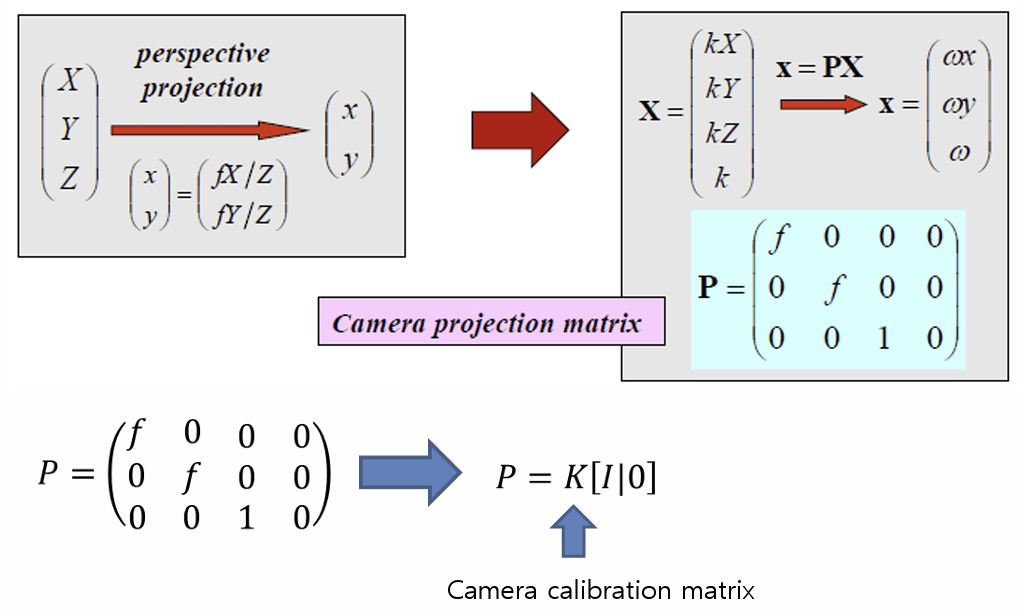
principal plane의 (0, 0)이 image plane의 (u0, v0)와 동일하다.
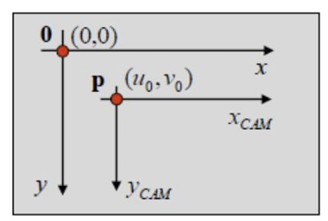
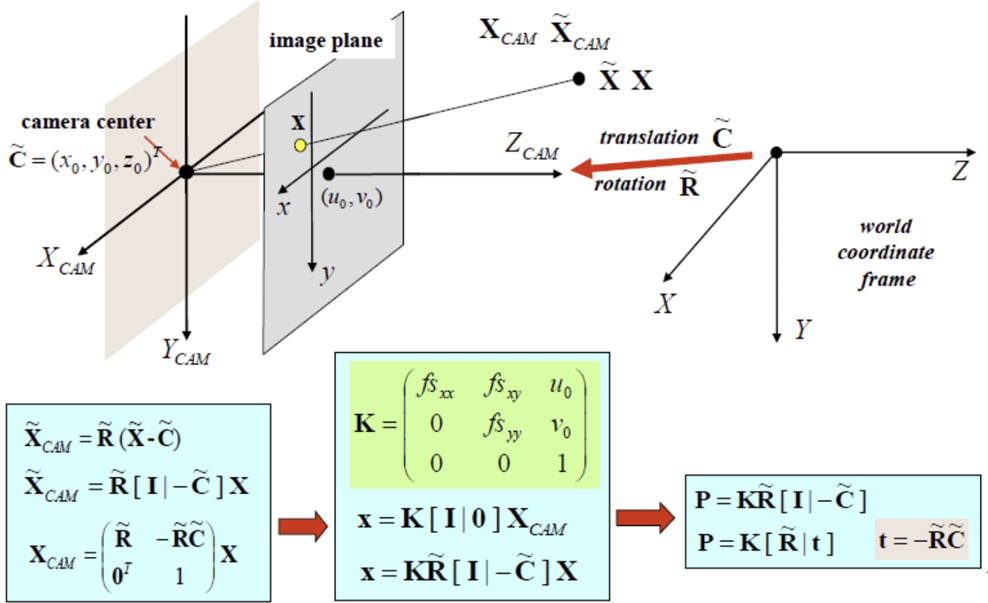
x, y는 실제 pixel 좌표 (image plane 상), Xcam, Ycam, 1은 principal point가 (0, 0)일 때의 좌표이다. skew parameter은 rotate/translate 변환 행렬이다.
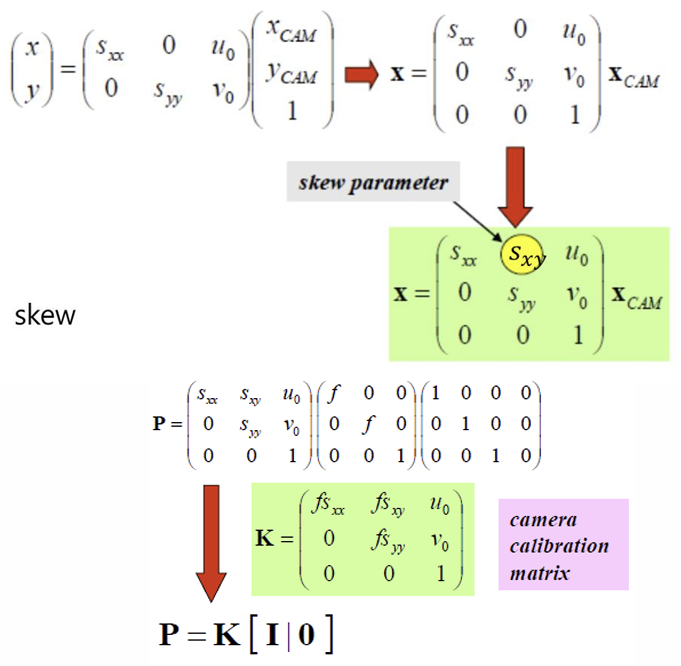
일반적인 카메라 모델에서는, world coordinate frame의 원점이 C만큼 translation 되고 R만큼 rotation 된다.