- source : https://www.youtube.com/watch?v=rmVRLeJRkl4&list=PLoROMvodv4rOSH4v6133s9LFPRHjEmbmJ&index=1&t=2671s

Usable meaning in a computer
WordNet(thesaurus containing lists of synonym sets and hypernyms)
- hypernyms → “is a” relationships(단점) missing nuance, impossible to up-to-date (missing new meaning of words)
Traditional NLP의 문제점
- words are regarded as discrete symbols :
one-hot vector - vector dimension = number of words in vocab

→ No similarity, relationships because two vectors are orthogonal
⇒ (해결책) learn to encode similarity in the vectors themselves with DL
Representing words by their context
- Distributional semantics(분포상의 의미) ↔ denotational semantics(글자 표기상의 의미)
→ A word’s meaning is given by the words that frequently appear close-by.
→ “context”의 중요성 (within a fixed-size window)
→ modern statistical NLP의 가장 성공적인 아이디어 중 하나
📌 “You shall know a word by the company it keeps.” (J.R.Firth)
-
2 senses of words :
tokens: 문장에 나온 하나의 단어를 가리키는 것types: tokens들을 많이 모았을 때, 여러 사례에서 사용하는 용도와 의미를 가리키는 것
-
(1) Word vectors: dense vector for each word→ 비슷한 문맥의 단어들끼리는 word vectors의 value가 비슷함
→ dot(scalar) product로 similarity 측정
→ 일반적으로 300-dimension으로 표현
(2) word embeddings: when we have a whole bunch of words, representations place in a high dimensional vector space. → they’re embedded into that vector space.(3) (neural) word representations(4) distributed representation(↔ localized representation)

시각화해서 보면, distributionally learned되어 비슷한 단어들끼리 잘 grouping되어 있음
Word2vec (Mikolov et al. 2013)
-
framework for learning word vectors
-
아이디어
- 고정된 개수의 vocab에 있는 모든 단어는 vector로 표현됨
- text 가 이동하면서, 모든 단어는 2가지 유형의 단어를 가짐
- center word
- context word(”outside”)
- 단어 출현 빈도에 따라 계산 ⇒ maximize
-
(ex) 계산 (window = 2)
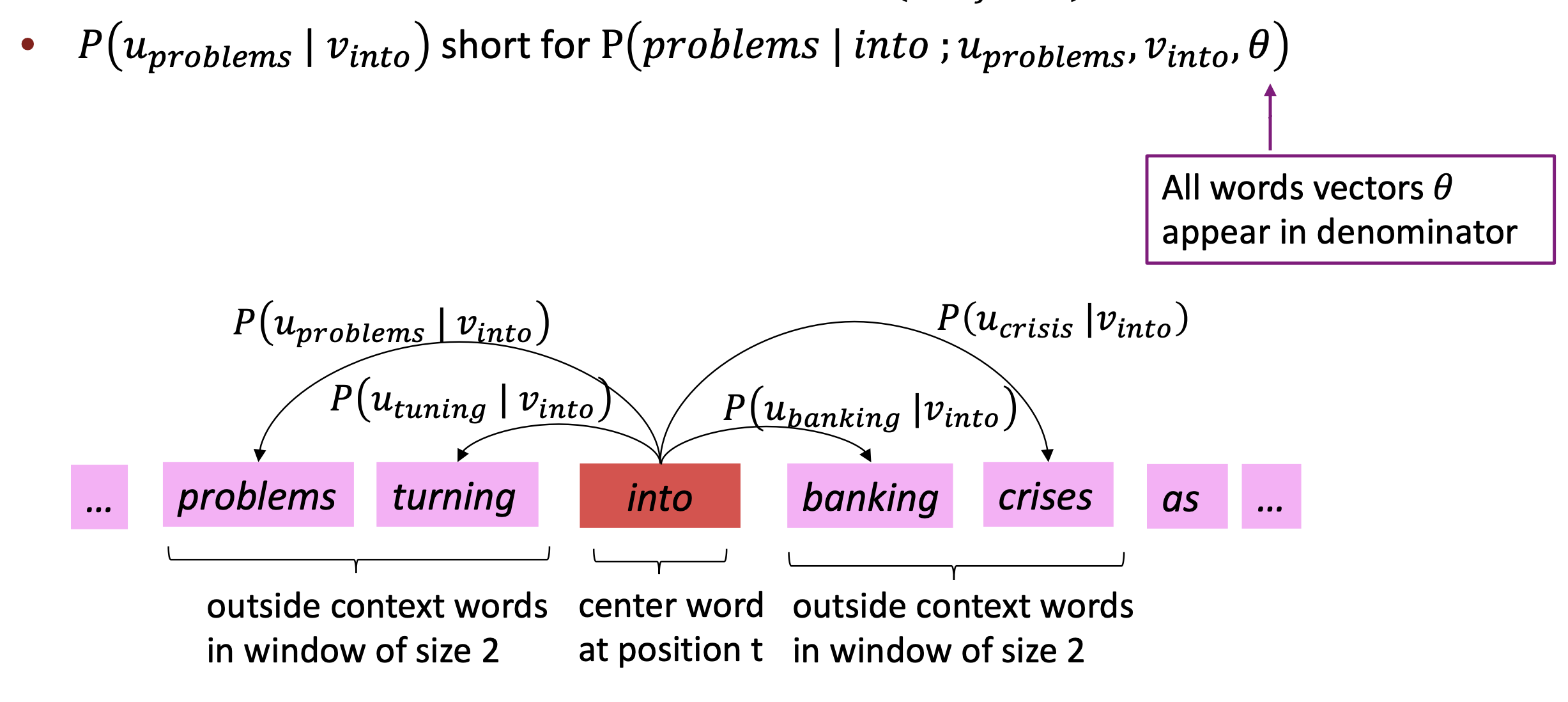
- Likelihood function
- predict context words within a window of fixed size
- , window size , center word
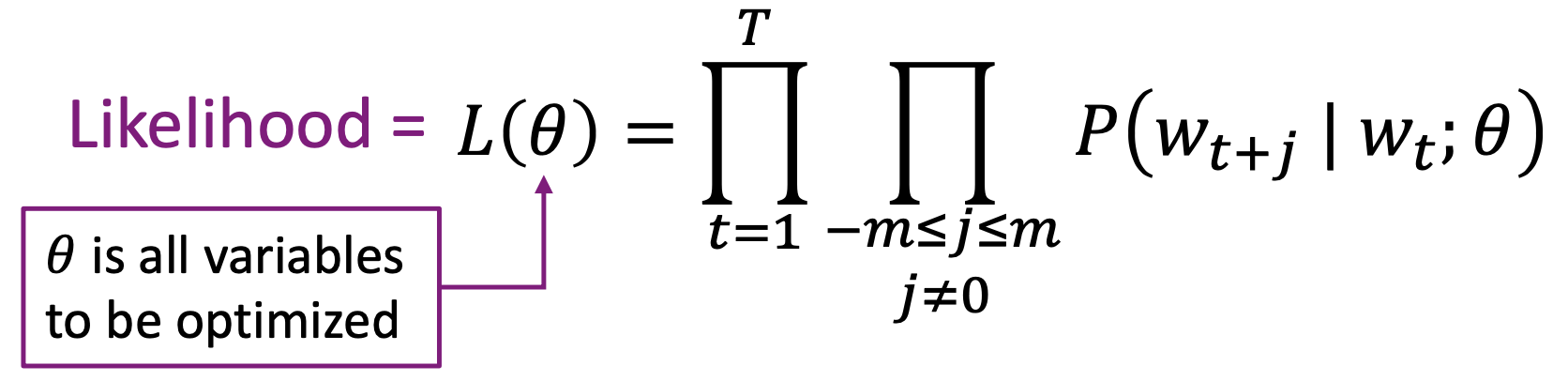
- objective function (cost or loss function)
- (average) negative log likelihood
- 곱셈을 덧셈으로 바꿔주기 위해 log를 취하고, 평균을 위해 1/T를 곱해줌
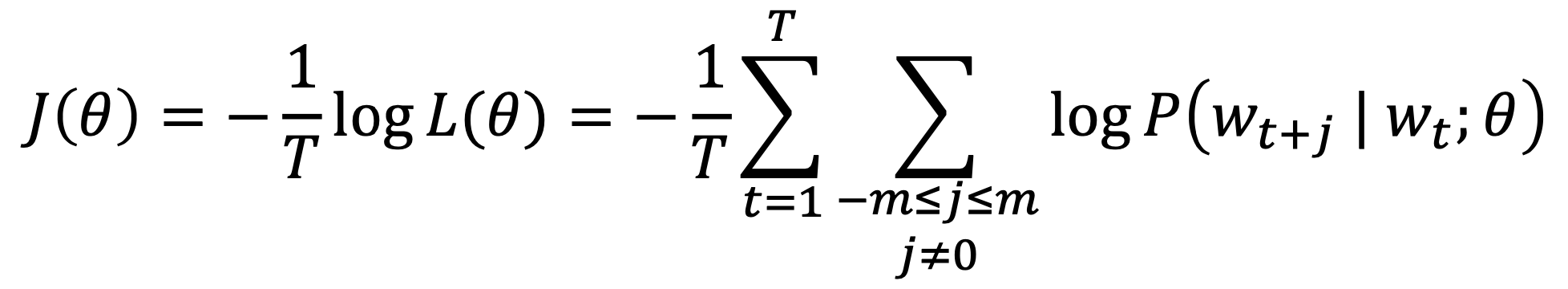
📌 Minimizing objective function = Maximizing predictive accuracy
- How to calculate ?
- Use two vectors per word
- : is a center word
- : is a context word
- center word , context word
- 분자 : 하나의 context word vector와 하나의 center word vector가 곱해진 값
- 분모 : vocab에 있는 모든 context word vector와 하나의 center word vector가 곱해진 값
- Use two vectors per word
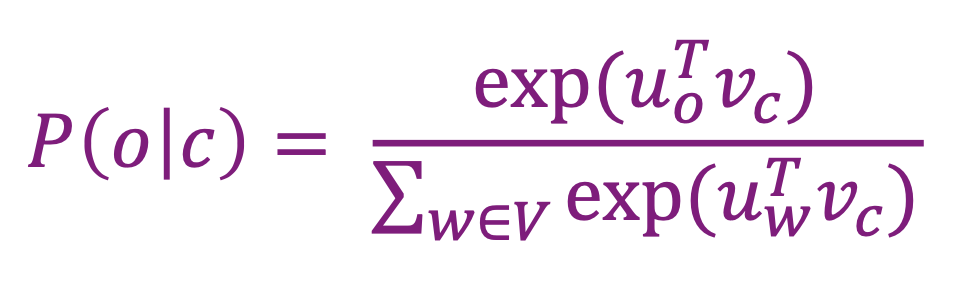
-
numerator(분자)
- Dot product compares similarity of o and c vector
- Larger dot product = Larger probability = more similar
-
exponentiation makes anything positive
- 1번의 결과는 +/- 둘 다 가능한데, 우리는 probability를 원하기 때문에 exp 적용
- (cf) negative probability는 존재 X
-
denominator(분모)
- probability distribution을 얻기 위해 전체 vocab에 대해 Normalization
- 다 더하면 1의 값이 나올 수 있게!
📌 Word2vec의 prediction function ⇒ [softmax function] → 의 예시
- maps arbitrary values to a probability distribution
- “soft” : still assigns some probability to smaller
- “max” : amplifies probability of largest
Train the model
-
Optimize parameters to minimize loss
= Maximize the prediction of context words -
: all the model parameters (= word vectors)
⇒ compute all vector gradients
-
(ex) d = 300, V = 500,000
-
every word has two vectors
- center vector
- context vector
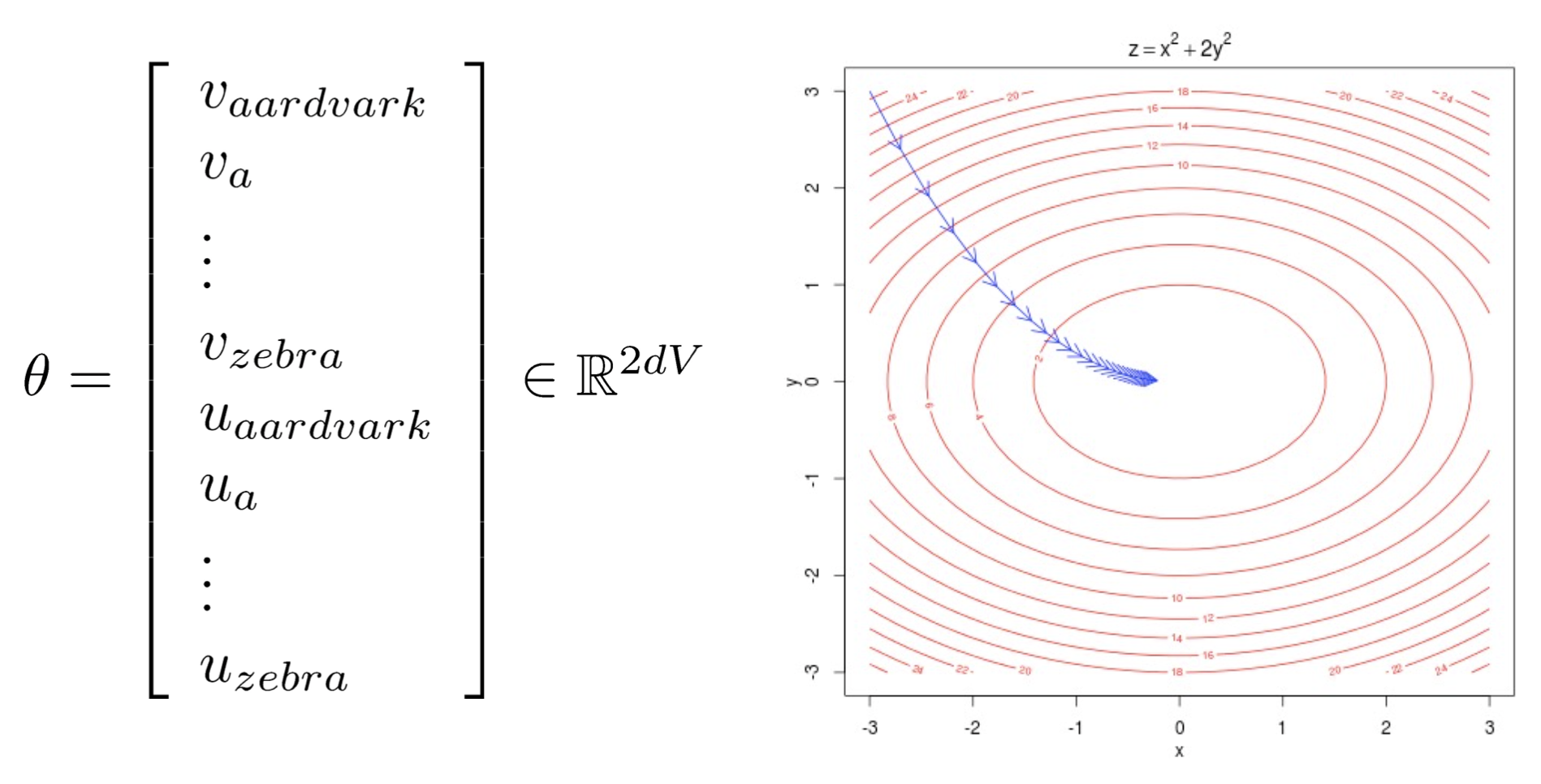
objective function의 를 미분해보자
- 를 이용할 것
-
numerator
-
denominator
- 합성함수 미분하듯, chain rule 이용
- 합성함수 미분하듯, chain rule 이용
- 정리해보면,
-
expectation average over all context vectors weighted by their probability
-
-
고민해볼 점
-
vector들 간의 계산으로 유사도를 구할 수 있는 건 알겠는데, vector를 표현하는 values는 어떻게 생성되는가?
→ initialized randomly (starting point)
→ iterative algorithm (progressively updating those word vectors using gradients)
→ better job at predicting which words appear in the context of other words
