힙 정렬(heap sort)

임동민·2022년 7월 22일

알고리즘

목록 보기

4/12

자료구조 ‘힙(heap)’

완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
최댓값, 최솟값을 쉽게 추출할 수 있는 자료구조

힙 정렬(heap sort) 알고리즘의 개념 요약

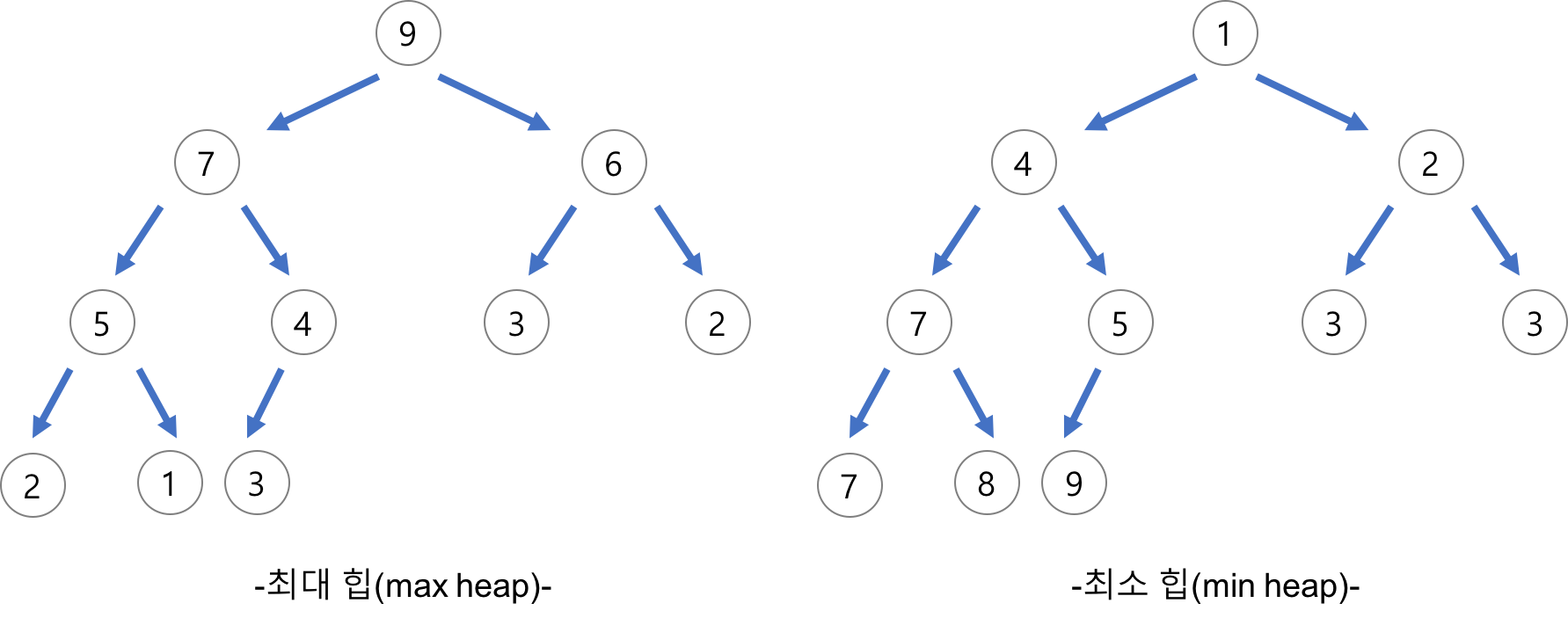
최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법
내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 된다.
과정 설명

정렬해야 할 n개의 요소들로 최대 힙(완전 이진 트리 형태)을 만든다.

내림차순을 기준으로 정렬

그 다음으로 한 번에 하나씩 요소를 힙에서 꺼내서 배열의 뒤부터 저장하면 된다.
삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게 된다.

내림차순 정렬을 위한 최대 힙(max heap)의 구현

힙(heap)은 1차원 배열로 쉽게 구현될 수 있다.
정렬해야 할 n개의 요소들을 1차원 배열에 기억한 후 최대 힙 삽입을 통해 차례대로 삽입한다.
최대 힙으로 구성된 배열에서 최댓값부터 삭제한다.

1. 최대 힙(max heap)의 삽입

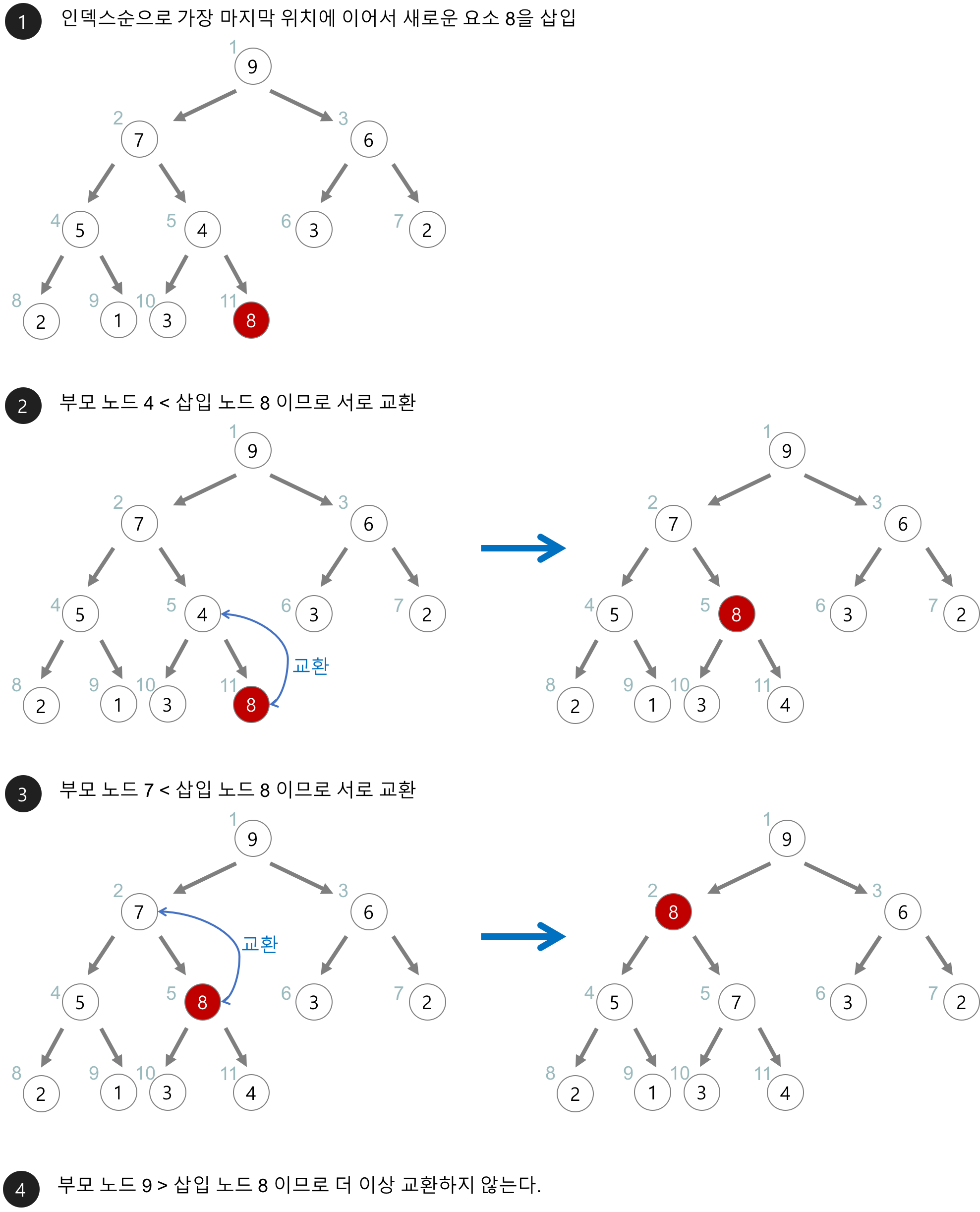
힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.

아래의 최대 힙(max heap)에 새로운 요소 8을 삽입해보자.

c언어를 이용한 최대 힙(max heap) 삽입 연산

/* 현재 요소의 개수가 heap_size인 힙 h에 item을 삽입한다. */
// 최대 힙(max heap) 삽입 함수
void insert_max_heap(HeapType *h, element item){
  int i;
  i = ++(h->heap_size); // 힙 크기를 하나 증가

  /* 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정 */
  // i가 루트 노트(index: 1)이 아니고, 삽입할 item의 값이 i의 부모 노드(index: i/2)보다 크면
  while((i != 1) && (item.key > h->heap[i/2].key)){
    // i번째 노드와 부모 노드를 교환환다.
    h->heap[i] = h->heap[i/2];
    // 한 레벨 위로 올라단다.
    i /= 2;
  }
  h->heap[i] = item; // 새로운 노드를 삽입
}

2. 최대 힙(max heap)의 삭제

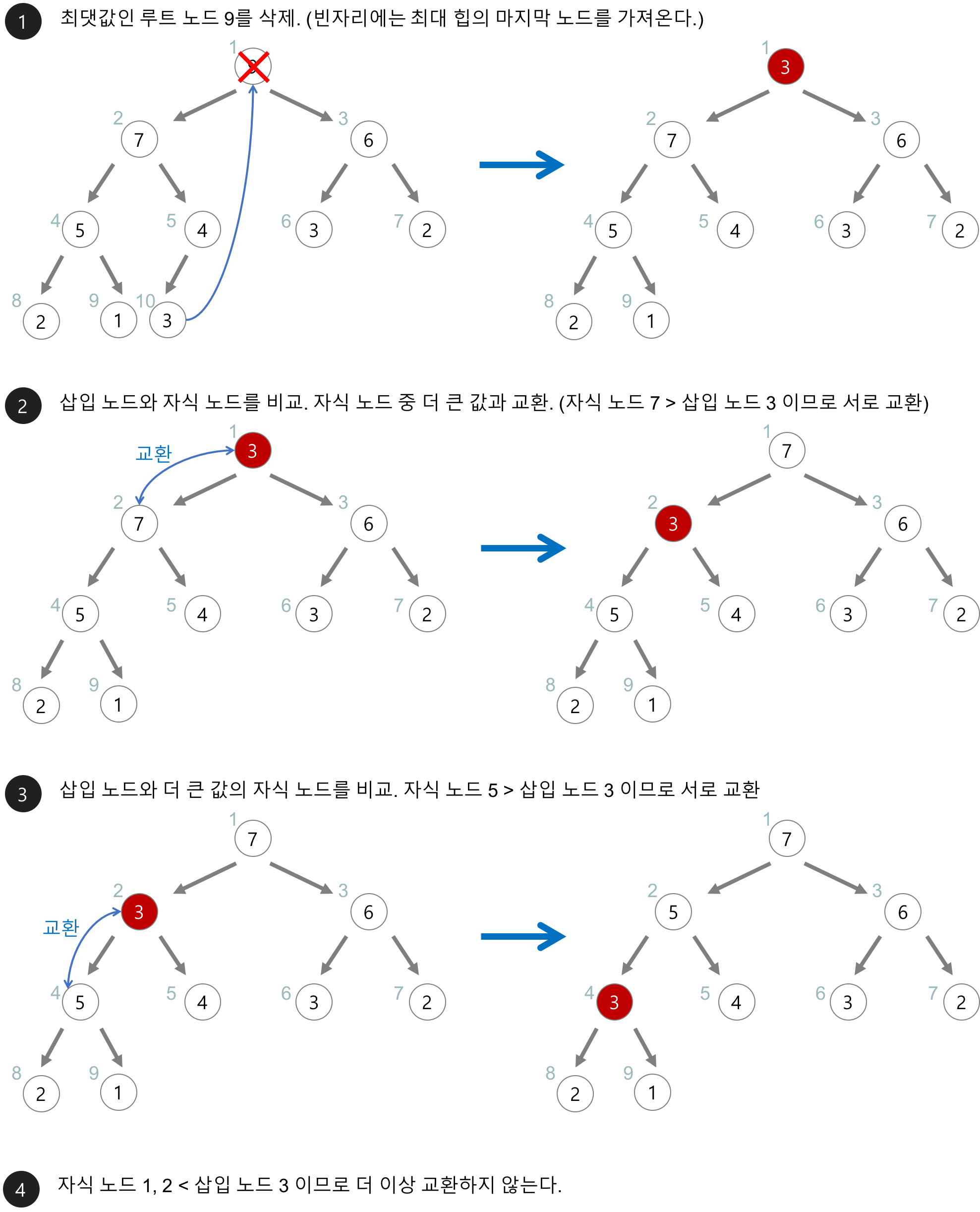
최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.

최대 힙(max heap)에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.

삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
힙을 재구성한다.

아래의 최대 힙(max heap)에서 최댓값을 삭제해보자.

c언어를 이용한 최대 힙(max heap) 삭제 연산

// 최대 힙(max heap) 삭제 함수
element delete_max_heap(HeapType *h){
  int parent, child;
  element item, temp;

  item = h->heap[1]; // 루트 노드 값을 반환하기 위해 item에 할당
  temp = h->heap[(h->heap_size)--]; // 마지막 노드를 temp에 할당하고 힙 크기를 하나 감소
  parent = 1;
  child = 2;

  while(child <= h->heap_size){
    // 현재 노드의 자식 노드 중 더 큰 자식 노드를 찾는다. (루트 노드의 왼쪽 자식 노드(index: 2)부터 비교 시작)
    if( (child < h->heap_size) && ((h->heap[child].key) < h->heap[child+1].key) ){
      child++;
    }
    // 더 큰 자식 노드보다 마지막 노드가 크면, while문 중지
    if( temp.key >= h->heap[child].key ){
      break;
    }

    // 더 큰 자식 노드보다 마지막 노드가 작으면, 부모 노드와 더 큰 자식 노드를 교환
    h->heap[parent] = h->heap[child];
    // 한 단계 아래로 이동
    parent = child;
    child *= 2;
  }

  // 마지막 노드를 재구성한 위치에 삽입
  h->heap[parent] = temp;
  // 최댓값(루트 노드 값)을 반환
  return item;
}

힙 정렬(heap sort) 알고리즘의 예제 및 c언어 코드

배열에 9, 7, 6, 5, 4, 3, 2, 2, 1, 3이 저장되어 있다고 가정하고 자료를 내림차순으로 정렬해 보자.
위의 최대 힙(max heap)의 삽입, 삭제 c언어 코드를 참고하자.

// 우선순위 큐인 힙을 이용한 정렬
void heap_sort(element a[], int n){
  int i;
  HeapType h;

  init(&h);

  for(i=0; i<n; i++){
    insert_max_heap(&h, a[i]);
  }

  for(i=(n-1); i>=0; i--){
    a[i] = delete_max_heap(&h);
  }
}