자료구조 - Graph , Tree ,BST

Graph (그래프)

규칙성 없이 연결하여 사용하는 비선형 구조의 자료구조이다.
그래프는 하나하나의 객체(node) 를 표현하는 정점(vertex)과 그 정점들을 연결하는 간선(edge)로 이루어 져 있다.

이 간선에서 방향이 없이 연결되어 있으면 무방향 그래프, 간선이 화살표처럼 방향이 정해져 있으면 방향 그래프 라고 한다.

알아야 할 그래프 용어

1. 무향그래프(undirected graph) - 방향이 없는 그래프이다. 간선이 변으로 이루어져 있다.

2. 유향 그래프(directed graph) - 방향이 있는 그래프이다. 출발 노드와 도착 노드로 구분되고 간선이 화살표 모양.
   2-1. 진입 차수(in-degree) - 유향 그래프에서 한 정점에 진입하는 차수가 몇개인지 나타낸다.
   2-2. 진출 차수(out-degree)- 유향 그래프에서 한 정점에서 진출하는 차수가 몇개인지 나타낸다.

3. 인접성(adjacency)
   3-1 무향 그래프의 인접성 - 두개의 정점이 간선으로 연결되어 있으면 "인접해 있다"라고 한다.
   3-2 유향 그래프의 인접성 - 두개의 정점이 간선으로 연결되어 있을때, 간선의 방향에 따라 "~로 인접해있다" , "~로부터 인접해있다" 라고한다.

4. 자기 루프(self loop) - 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다 라고 표현한다.

5. 사이클 - 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다.

Tree (트리)

나무가 하나의 뿌리 노드(root node)로 부터 하위 레벨(lower level)로 가지가 나오는 집합 관계를 갖는 계층 구조를 말한다.

Tree는 데이터를 순차적으로 나열시킨 선형 구조가 아닌, 하나의 데이터 뒤에 여러개의 데이터가 존재할 수 있는 비선형 구조로 되어있고, 계층적으로 표현이 되며 아래로만 뻗어가기 때문에 사이클이 없다.

Binary Tree (이진 트리)

자식 노드가 최대 두 개인 노드로 구정된 트리를 이진 트리라고 하는데, 이 두 개의 노드는 왼쪽 자식과 오른쪽 자식으로 분류한다.

이진 트리는 데이터의 삽입, 삭제 방법에 따라 다음과 같이 분류할 수 있다.

• 정 이진 트리(Full binary tree)
• 완전 이진 트리 (Complete binary tree)
• 포화 이진 트리 (Perfect binary tree)

정 이진 트리는 각 노드가 0개 혹은 2개의 자식 노드를 가져야 한다.

완전 이진 트리는 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽부터 채워져야 한다

포화 이진 트리는 위의 두 트리의 조건이 모두 충족되는 트리이다.

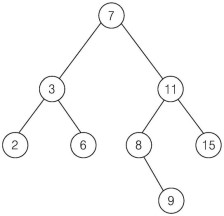
Binary Search Tree (이진 탐색 트리)

BST 는 이진트리 구조에서 출발하고, 데이터의 삽입, 삭제, 탐색 등이 자주 발생하는 경우에 효율적인 구조이다.

BST 는 이진트리에 4가지 조건을 더 갖는 트리 구조이며 조건은 아래와 같다.

• 모든 노드는 다른 값을 갖는다.
• 왼쪽 서브 트리의 데이터 값은 부모 노드의 데이터 값보다 작은 값을 갖는다.
• 오른쪽 서브 트리의 데이터 값은 부모 노드의 데이터 값보다 큰 갖는다.
• 왼쪽, 오른쪽 서브트리도 이진 탐색 트리이다.

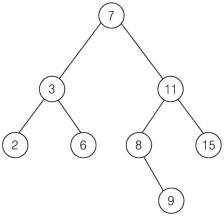
왼쪽 서브 트리에 있는 모든 데이터는 현재 노드의 값보다 작고, 오른쪽 서브 트리에있는 모든 노드의 데이터는 현재 노드의 값보다 크다.