[알고리즘] CCW

eunbi·2022년 8월 17일

알고리즘

목록 보기

2/11

CCW

CCW가 도대체 뭘까싶었다. Counter ClockWise(시계반대방향)의 약자이다. 그럼 이게 도대체 어디에 쓰이는가? 이걸로 세 점이 있을 때 방향성을 나타낼 수 있다.
벡터 외적의 특성과 고등학교 물리 시간에 배우는 오른손 법칙을 사용하여 이것을 증명할 수 있다.

오른손 법칙

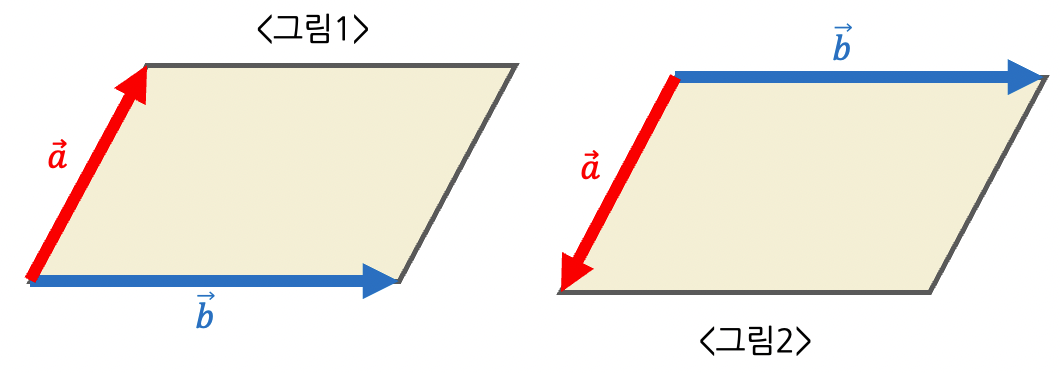
1. 오른손을 펴서, <그림1>에서 벡터 a가 가리키는 방향으로 손날을 놓아보자.
2. 이때 벡터 b의 방향으로 손가락을 굽혀보자. 어이쿠 손을 반대로 꺾을 순 없다. 따라서 손날을 반대로, 엄지손가락이 바닥을 향하도록 벡터 a에 놓아보자. 그리고 손가락을 벡터b 방향으로 말아보면 잘 말아진다.
3. 다음으로 <그림2>에서 벡터 a가 가리키는 방향으로 손날을 놓아본다. 손목이 날 향해있어서 아프지만 한 번 해보자.
4. 그 상태로 벡터 b 방향으로 말아보자.
5. 두 그림에서 모두 손가락을 말아보았다. 하지만 차이점이 있다. 바로 엄지손가락이 향하는 방향이다. <그림1>에서는 엄지손가락이 바닥을 향했지만, <그림2>에서는 엄지손가락이 하늘을 향한다. 오른손 법칙에서 엄지손가락이 향하는 방향, 이것이 바로 벡터a, 벡터b의 법선 벡터 방향이다!! (*법선벡터 : 두 벡터와 수직인 벡터)

벡터의 외적

그렇다면 벡터의 외적은 무엇인가를 알아야 한다. a, b 두 벡터의 외적이란 $\vec{a}\times\vec{b}$ 을 뜻하고 이 외적의 방향은 a, b 벡터의 수직이다. 어라 위에서 구한 두 벡터의 법선벡터와 방향이 똑같다! 그렇다면 오른손 법칙으로 벡터의 외적 방향을 구할 수 있을 것이다. 이어서 외적의 크기는 $\vert\vec{a}\vert\vert\vec{b}\vert\sin{\theta}$ 이다. 이를 그림에서 살펴보자.

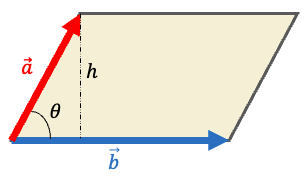
$\sin{\theta}={h}/{\vert\vec{a}\vert}$ 으로 나타낼 수 있다. 따라서 해당 식을 외적의 크기 식에 대입한다면 $\vert\vec{b}\vert*h$ 가 나온다. 평행사변형의 넓이는 밑변과, 그 높이로 구할 수 있다. 따라서 앞선 식은 $\vert\vec{b}\vert$ 를 밑변으로 하고 높이가 $h(=\sin{\theta}*\vert\vec{a}\vert)$ 인 평행사변형의 넓이인 것이다. 즉 외적의 크기가 두 a, b벡터가 이루는 평행사변형의 넓이와 똑같다는 것을 알 수 있다!

추가적으로 벡터의 외적 공식이 있다.

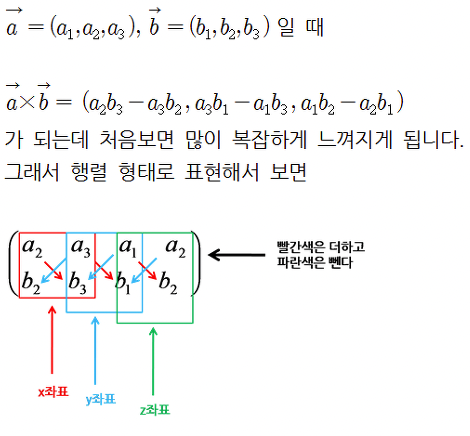
왜 그런진 모르겠다. 저렇게 신발끈 모양으로 냅다 외웠다. (미안. 미안합니다. 쏘리는 해)

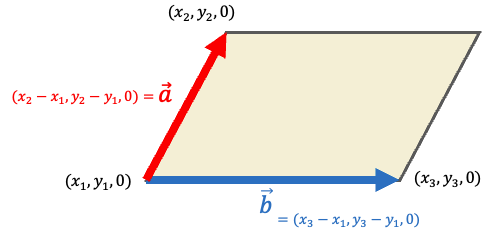
그렇다면 앞의 그림에 적용해보자. 세 점을 저렇게 두면 벡터 또한 구할 수 있다. (z좌표는 0이다. ~~당연함 2차원임~~). 이제 진짜 공식에 적용해서 외적을 구해보면 $=(0, 0, (x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1))$ 이다. 즉 $(x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1)$ 이 외적 방향이 된다!!

앞서 배운 세가지를 정리하면 다음과 같다.
1. 오른손 법칙으로 벡터의 외적 방향을 구할 수 있다.
2. 외적의 크기는 두 벡터가 이루는 평행사변형의 넓이와 똑같다.
3. $(x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1) = (x_1y_2+x_2y_3+x_3y_1)-(x_1y_3+x_2y_1+x_3y_2)$ 이 외적 방향을 나타낸다.

이를 이용해 무려 두 가지 타입의 문제를 풀 수 있다!!

예제

두 직선의 교차 여부 판단

백준 17387 선분교차2 - [풀이]

2차원 좌표 평면 위의 두 선분 L1, L2가 주어졌을 때, 두 선분이 교차하는지 아닌지 구해보자.
한 선분의 끝 점이 다른 선분이나 끝 점 위에 있는 것도 교차하는 것이다.
L1의 양 끝 점은 (x1, y1), (x2, y2), L2의 양 끝 점은 (x3, y3), (x4, y4)이다.

세 점을 두 벡터로 나타낼 수 있다.
: 그렇다면 (L1의 점 두 개-L2의 점 하나)(L1의 점 두 개-L2의 나머지 점 하나), (L2의 점 두 개-L1의 점 하나)(L2의 점 두 개-L1의 나머지 점 하나) 일단 이렇게 벡터를 나눠보자.
두 벡터가 이루는 방향은 외적의 방향으로 구할 수 있다. (시계 또는 반시계) - (1)

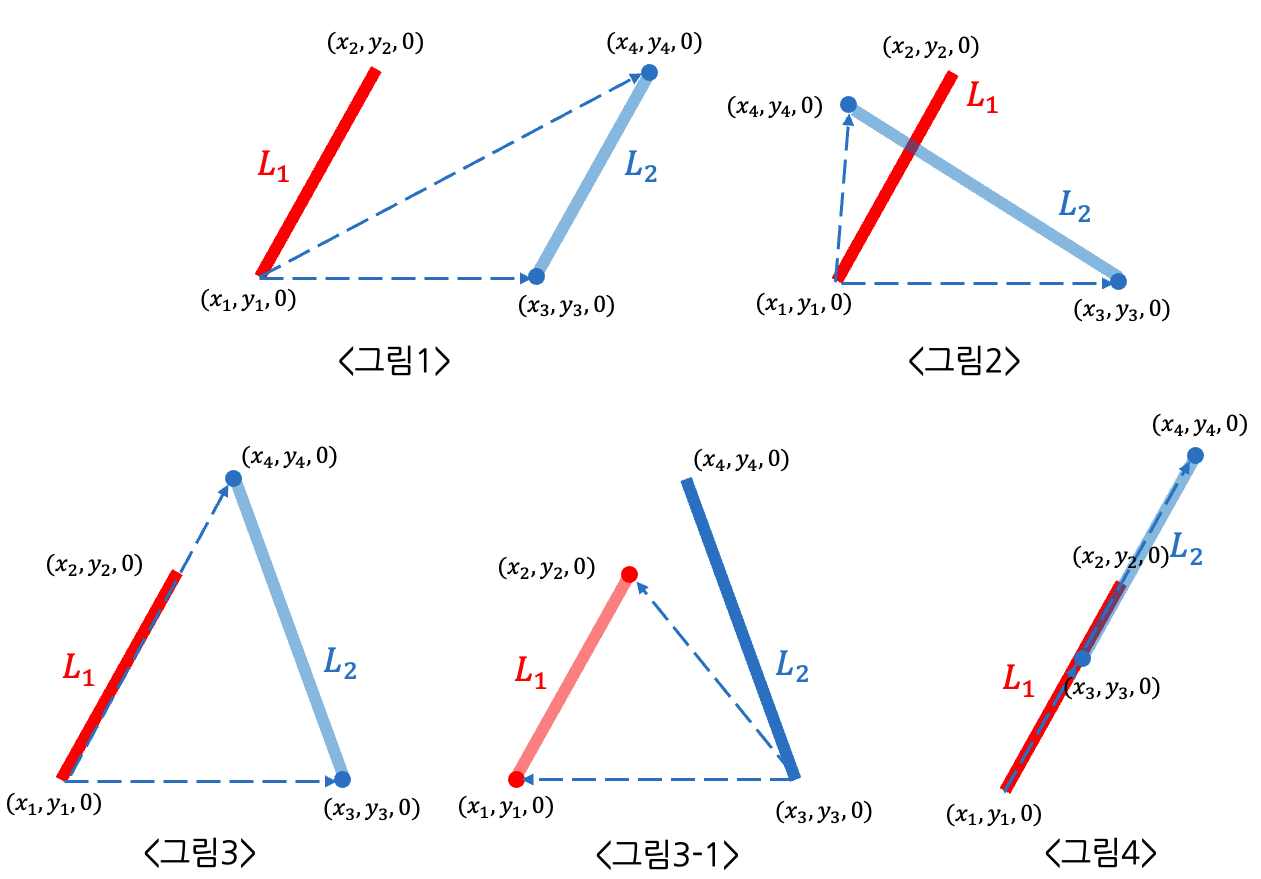
: 1에서 말한 L1의 점 두개-L2의 점 하나/L2의 나머지 점 하나를 나타낸 그림들이다.

외적의 방향은 $(x_1y_2+x_2y_3+x_3y_1)-(x_1y_3+x_2y_1+x_3y_2)$ 이다. - (3)
: 이제 위 그림에 나타난 두가지 벡터의 외적의 방향을 구할 수 있다. 그림이 있으므로 그림을 보고 바로 방향성을 판단해보자.

그림	벡터	방향성(ccw)	방향성 곱하기(ccw*ccw)
그림1	L1 점 두 개와, 점4	시계(-)
그림1	L1 점 두 개와, 점3	시계(-)	(-)*(-)=(+)
그림2	L1 점 두 개와, 점4	시계(-)
그림2	L1 점 두 개와, 점3	반시계(+)	(-)*(+)=(-)
그림3	L1 점 두 개와, 점4	0
그림3	L1 점 두 개와, 점3	시계(-)	(0)*(-)=(0)
그림3-1	L2 점 두 개와, 점2	반시계(+)
그림3-1	L2 점 두 개와, 점1	반시계(+)	(+)*(+)=(+)
그림4	L1 점 두 개와, 점4	0
그림4	L1 점 두 개와, 점3	0	(0)*(0)=(0)

이제 그림들이 뭘 뜻하는지 살펴보자. <그림1> 두 직선이 평행하다(교차하지 않는다). <그림2> 두 직선이 교차한다. <그림3> 두 직선 교차하지 않는다. <그림4> 두 직선이 나란히 겹쳐있다. 이제 각자의 곱하기 결과와 비교해보자. (위에서 그림3을 제외한 나머지는 L1만을 기준으로 구했다. L2 기준으로는 따로 구해서 테이블에 넣어주었다.)

그림	곱하기_L1	곱하기_L2	모양새
그림1	+	+	평행, 교차X
그림2	-	-	교차O
그림3	0	+	교차X
그림4	0	0	겹침, 교차O

여기서 특징이 보이는가? ccw 곱하기(l1), ccw 곱하기(l2) 이 둘 다 0 이하일 때만 교차한다! 이로 두 직선이 교차하는지 안 하는지 알아낼 수 있다.

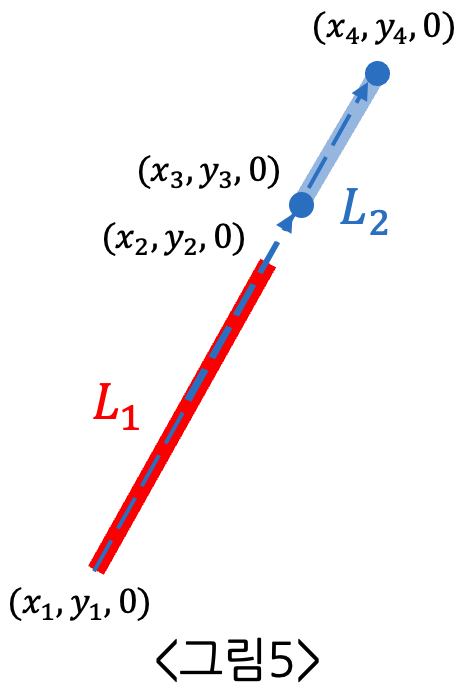
(위 그림과 같이 0, 0 이지만 교차하지 않을 때도 있다. 이는 따로 점들의 위치를 파악해 알아낸다.)

세 점이 이루는 삼각형의 넓이 구하기

백준 2166 다각형의면적 - [풀이]

2차원 평면상에 N(3 ≤ N ≤ 10,000)개의 점으로 이루어진 다각형이 있다. 이 다각형의 면적을 구하는 프로그램을 작성하시오.

세 점을 벡터로 나타낼 수 있다.
외적의 크기는 벡터가 이루는 평행사변형의 넓이이다.
평행사변형을 반으로 나누면 그 벡터가 이루는 삼각형의 넓이가 된다.

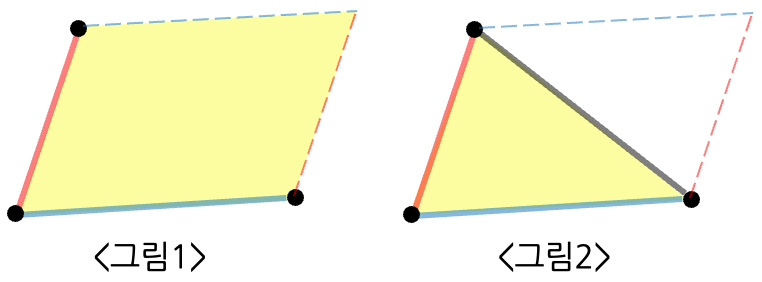
위 세 요소를 합쳐보자. 이제 세 점의 위치만 알면 외적의 크기를 구할 수 있고, 이 외적의 크기(평행사변형-그림1)을 반으로 나누면 세 점이 이루는 삼각형의 넓이가 된다!

eunbi

이전 포스트

[알고리즘] dx dy

다음 포스트