이분탐색
정렬된 리스트에서 특정값을 찾는 방법. 순차 탐색과 달리 탐색 범위를 절반씩 좁혀가며 탐색을 진행하기 때문에 계산횟수가 줄어든다.

- 원소 찾기 (아래 코드는 정렬된 리스트에 존재하는 값만을 찾을 때 만족된다.)
int binary_search(vector<int> arr, int key) {
int low = 0;
int high = arr.size();
while (low <= high) {
int mid = (low + high) / 2;
if (key == arr[mid]) {
low = mid;
break;
}
else if (key < arr[mid]) {
high = mid;
}
else {
low = mid + 1;
}
}
return low;
}예제
중복 원소의 개수 구하기
lower bound / upper bound
-
lower bound(하한) : 찾으려고 하는 값 이상의 값이 처음 나타나는 위치
eg1) [2, 4, 7, 7, 8, 11] 에서 7의 lower bound : 2 ( 인 값 중 제일 앞에 있는 7이, idx2이므로)
eg2) [2, 4, 8, 9, 11] 에서 7의 lower bound : 2 ( 인 값 중 제일 앞에 있는 8이, idx2이므로) -
upper bound(상한) : 찾으려고 하는 값 초과의 값이 처음 나타나는 위치
eg1) [2, 4, 7, 7, 8, 11] 에서 7의 upper bound : 4 ( 인 값 중 제일 앞에 있는 8이, idx4이므로)
eg2) [2, 4, 8, 9, 11] 에서 7의 lower bound : 2 ( 인 값 중 제일 앞에 있는 8이, idx2이므로) -
그렇다면 lower, upper bound 로 어떻게 중복 원소의 개수를 구할까? lower bound는 이상을 의미하고 upper bound는 초과를 뜻하기 때문에, upper에서 lower를 빼면 초과-이상에 중복되는 값들이 모두 제거된다. 즉, 초과와 이상의 차이는 그 기준값이 같을 때 뿐이므로 우리가 찾는 값의 개수가 자연스럽게 나온다.
eg1) [2, 4, 7, 7, 8, 11] → 4-2 = 2개! -
만약 찾는 값이 존재하지 않을 때도 이는 적용된다.
eg2) [2, 4, 8, 9, 11] → 2-2 = 0개! -
lower bound, upper bound 를 구하기 위한 이진탐색 코드는 다음과 같다.
int lower_Bound(vector<int> arr, int key) {
int low = 0;
int high = arr.size();
while (low < high) {
int mid = (low + high) / 2;
if (key <= arr[mid]) { /*** <= ***/
high = mid;
}
else {
low = mid + 1;
}
}
return low;
}
int upper_Bound(vector<int> arr, int key) {
int low = 0;
int high = arr.size();
while (low < high) {
int mid = (low + high) / 2;
if (key < arr[mid]) { /*** < ***/
high = mid;
}
else {
low = mid + 1;
}
}
return low;
}- cpp에선 STL을 지원한다.
vector<int> arr = {2, 4, 7, 7, 9, 11};
int num_of = upper_bound(arr.begin(), arr.end(), 7) - lower_bound(arr.begin(), arr.end(), 7);파라메트릭 서치(parametric search) ☑️
최적화 문제(문제의 상황을 만족하는 특정 변수의 최솟값, 최댓값을 구하는 문제)를 결정 문제로 바꾸어 푸는 것.
집에서 시간을 보내던 오영식은 박성원의 부름을 받고 급히 달려왔다.
박성원이 캠프 때 쓸 N개의 랜선을 만들어야 하는데 너무 바빠서 영식이에게 도움을 청했다.
이미 오영식은 자체적으로 K개의 랜선을 가지고 있다. 그러나 K개의 랜선은 길이가 제각각이다.
박성원은 랜선을 모두 N개의 같은 길이의 랜선으로 만들고 싶었기 때문에 K개의 랜선을 잘라서 만들어야 한다.
예를 들어 300cm 짜리 랜선에서 140cm 짜리 랜선을 두 개 잘라내면 20cm는 버려야 한다. (이미 자른 랜선은 붙일 수 없다.)
편의를 위해 랜선을 자르거나 만들 때 손실되는 길이는 없다고 가정하며,
기존의 K개의 랜선으로 N개의 랜선을 만들 수 없는 경우는 없다고 가정하자.
그리고 자를 때는 항상 센티미터 단위로 정수길이만큼 자른다고 가정하자.
N개보다 많이 만드는 것도 N개를 만드는 것에 포함된다.
이때 만들 수 있는 최대 랜선의 길이를 구하는 프로그램을 작성하시오.- 최적화 문제 : 랜선을 일정한 간격으로 잘라 N개를 만들 수 있는 최대 랜선의 길이
- 결정 문제 : 랜선을 D만큼의 일정한 간격으로 잘랐을 때 랜선 N개를 만들 수 있는지
⇒ 즉, 위 결정 문제를 풀 때 D를 이분탐색으로 탐색하며 결정 문제도 만족하고, 최적화 문제도 만족하는 최적의 D를 찾으면 된다! (순차적으로 가능한 모든 D를 시뮬레이션하는 경우 시간이 많이 걸리기 때문)
-
처음 D를 선택할 수 있는 범위는 0(low)~현재 최대 랜선 길이(high) 이다. 그 사이 중간 길이(mid)를 구해 해당 D가 결정 문제를 만족하는지 살펴본다.
-
만약 만족하지 않는다면 (수 부족→자르는 길이를 더 짧게 만들어 수를 늘려야함) high를 mid값으로 설정해 범위를 줄인다. 만약 만족한다면 자르는 길이를 늘려도 결정 문제를 만족하는지 (최대 길이를 구해야하기 때문) 확인하기 위해 low를 mid+1로 설정해 범위를 줄인다. (mid는 이미 만족을 확인했으므로 +1)
-
이때 결정 문제 만족 여부를 판단할 때 두 Bound 중 어떤 방법을 사용해야할까?
lower bound(하한) : 찾으려고 하는 값(=결정 문제를 만족하는) 이상의 값이 처음 나타나는 위치
upper bound(상한) : 찾으려고 하는 값(=결정 문제를 만족하는) 초과의 값이 처음 나타나는 위치
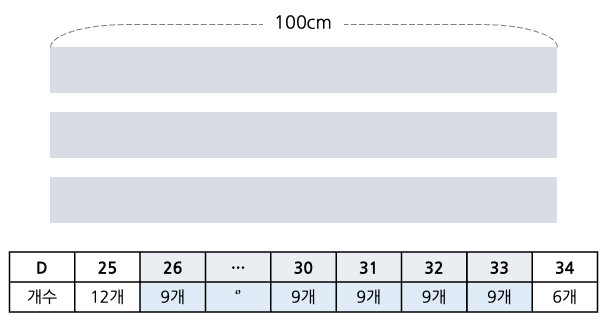
위 표는 100cm 랜선 3개를 가지고 있을 때 9개의 랜선을 만들기 위해 D를 계산한 결과이다. 26cm로 잘랐을 때 랜선은 9개가 되며 33cm로 잘랐을 때까지 결정 문제를 만족한다. 만약 이때 lower bound를 적용한다면 결과로 나오는 low는 26이고, upper bound를 적용한다면 low는 34이다. 우리는 9개를 만들 수 있는 최대 랜선의 길이를 구해야 하므로 26은 맞지않다. 따라서 upper bound를 적용해 34에서 하나를 뺀 값을 구해야한다. (low-1) -
💫 추가적으로 위 예시에서 1cm 랜선을 2개 가지고있다고 다시 가정하자. 그리고 2개의 랜선을 만들어야 한다고 가정하자. 과정은 다음과 같다.
low high mid 개수
0 1 0 0개 -> zerodivision zerodivision이 일어날뿐만 아니라 정답도 바르게 나오지 않는다. 하지만 만약에 초기 high값을 max+1로 설정한다면 어떨까.
low high mid 개수
0 2 1 2개
2 2 XXX 이번에는 답(low-1=1)도 올바르고 low<high 조건도 만족되기 때문에 수행이 올바르게 종료된다. 즉! 처음에 high를 +1 해주어 실행해준다.
- 100cm 랜선 3개를 가지고 있을 때 9개의 랜선을 만들기 위해 D를 계산하기 위한 과정은 다음과 같다.
| low | high | mid | 개수 |
|---|---|---|---|
| 0 | 101 | 50 | 6개 |
| 0 | 50 | 25 | 12개 |
| 26 | 50 | 38 | 6개 |
| 26 | 38 | 32 | 9개 |
| 33 | 38 | 35 | 6개 |
| 33 | 35 | 34 | 6개 |
| 33 | 34 | 33 | 9개 |
| 34 | 34 | XXX |
long long low = 0, high;
for (int i = 0; i < K; i++) {
cin >> list[i];
high = max(high, (long long)list[i]);
}
++high;
while (low < high) {
long long mid = (low+high)/2;
long long cnt = 0;
for (int i = 0; i < K; i++) {
cnt += list[i]/mid;
}
if (cnt < N) {
high = mid;
}
else {
low = mid+1;
}
}
cout << low-1;
