Posterior과 Bayesian

• 베이즈 정리?
  베이즈 정리는 아래와 같이 구성할 수 있으며, 각각의 역할을 잘 확인해 봐야 합니다!
  

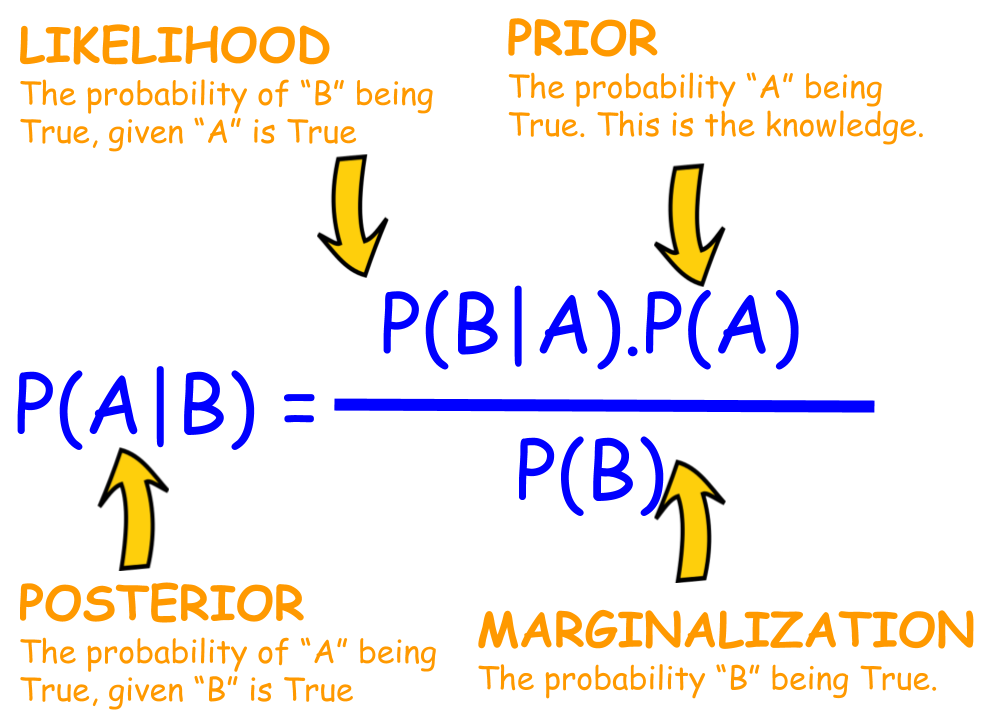
Posterior?
P(A|B) : 관측 값이 주어졌을 때 구하고자 하는 대상이 나올 확률로, 말 그대로 사후 확률입니다.

Likelihood?
P(B|A) : 구하고자 하는 대상이 정해졌다고 가정할 때, 주어진 대상이 나올 확률입니다.

Prior?
P(A) : 구하고자 하는 대상 자체에 대한 확률입니다.

그렇다면 이것들을 이용해서 베이즈정리를 구성하는 이유는 무엇일까요?
궁극적으로 구하고자 하는 것은 Posterior인 사후 확률 입니다. 하지만 이는 현실에서 쉽게 확률값을 구하기 어렵기에 Likelihood와 prior을 이용하여 베이즈 정리를 완성시키고, 이를 통해 사후 확률을 구하게 되는 것 입니다.

• P(B) 인 marginalization은 변하지 않는 상수에 해당되기에
  P(A|B) ∝ P(B|A) * P(A) 로 근사하게 됩니다.

ex 1) 주어진 대상 = 학습 데이터(D), 구하는 대상 = 모델 파라미터(w) 라고 했을 때,
=> Posterior = P(w|D) / Likelihood = P(D|w) / Prior = P(w) 가 되는 것 입니다.

ex 2) 신발 사이즈를 통해 남/여 를 맞출 때
주어진 대상 = 신발 사이즈, 구하는 대상 = 남/여 클래스
=> Posterior = P(성별|신발사이즈) / Likelihod = P(신발사이즈|성별) / Prior = P(성별)

Q. 그렇다면 MAP와 MLE는 무엇일까요?
MAP는 Posterior인 사후확률을 최대화 시키는 것 입니다. 여기서 베이즈 정리가 사용되며, likelihood와 prior을 곱하여 구하게 됩니다.

하지만 보통 prior을 구하는 것이 쉽지 않습니다.

그렇기에 균등분포라 가정하고 MAP가 아닌 likelihood를 최대화 시키는(최적의 파라미터w를 구하는 것) MLE로 접근하게 됩니다.

물론 두 방법 중 MAP가 더 정확하지만, 앞서 말한 prior을 구하기 어려운 이유로 MLE를 통해 근사시켜 쓸 때가 많습니다!

---

참고한 블로그에서 좋은 예시가 있기에 가져와 보겠습니다.

피부색 검출 문제로, 사진에서 피부색은 흰색, 아닌 부분은 검은색으로 classify 하는 예제 입니다.

피부색 검출을 위해 피부색 DB와 일반 색상 DB를 구성합니다.
입력 픽셀값이 z라 한다면,
Posterior = P(피부색|z) / Likelihood = P(z|피부색), P(z|일반색) 입니다.

MLE의 방법을 사용한다면, 어떤 임의의 픽셀 z가 왔을 때 P(z|피부색)와 P(z|일반색)를 비교하여 어떤 확률이 더 큰지 확인하고 그에 맞는 색을 선택하게 됩니다.
(여기서 P(z|피부색)은 피부색 DB에서 z와 같은 색을 갖는 데이터의 비율이며, P(z|일반색)은 일반색 DB에서 z와 같은 색을 갖는 데이터의 비율입니다)

MAP를 적용한다고 한다면, Prior을 알아야 합니다.
그렇다면 여기서 Prior인 P(피부색)과 P(일반색)은 무엇일까요?
P(피부색) = |피부색DB| / (|피부색DB|+|일반색DB|) 일까요? 이는 아닙니다.
=> P(피부색)는 세상에 존재하는 모든 이미지 색상들 중에서 피부색이 얼마나 되느냐를 나타내는 말입니다. 따라서 이 Prior 사전 확률을 추정하는 것은 무리가 있습니다. 이러한 다수의 경우들로 인해 MAP가 비교적 정확하지만, MLE를 사용하는 이유입니다.

참고 : https://aimaster.tistory.com/79
https://hwiyong.tistory.com/27