AVL Tree

AVL Tree는 앞 포스터의 Binary Search Tree의 depth가 너무 깊어지는 단점을 보완하고 balance를 맞추기 위해 등장했다.

무엇이 balance가 있는 것일까?

Balance factor (B) = HL−HR
Balanced binary tree : |B|≤1

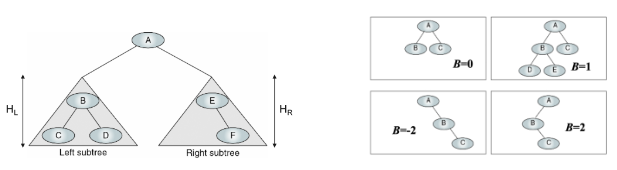
이와 같이 구성하여 BST의 단점을 보완하고자 한 것이다.

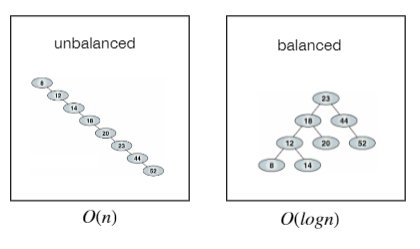
AVL Tree : a binary search tree in which for all nodes
(Georgy Maximovich Adelson-Velsky & Evgenii Mikhailovich Landis

아래와 같이 작성할 수 있으며, 양 옆의 자식 sub tree들을 기준으로 1 0 -1 이라고 표기가 가능하다. 여기서 이 숫자들을 넘어서면(ex) 2, -3) AVL tree라고 할 수 없게 되는 것이다.

LH (left high) : HL≥HR

EH (even high) : HL= HR

RH (right high) : HL≤HR

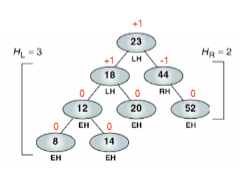
Insertion and Deletion

만약 아래와 같은 tree와 같이 밸런스가 깨졌다고 가정해보자. 이렇게 되면 AVL tree로 만들기 위해 어떠한 조치를 취해야 한다. 즉, -1, 0, 1로 변경시켜야 하는데, 이를 맞추기 위해 rotation을 통해 밸런스를 조정한다.

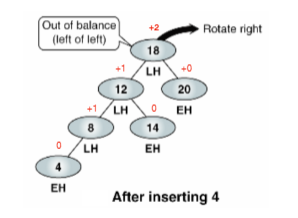
rotation은 아래와 같이 right left rotation이 존재한다.

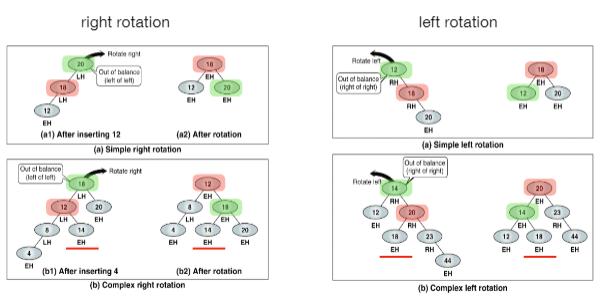
그렇다면 어떠한 상황에서 어떤 rotation을 적용시킬까?

rebalancing을 하기 위해 우선 현재 상태를 확인해야 하는데, 크게 4가지로 분류할 수 있다.

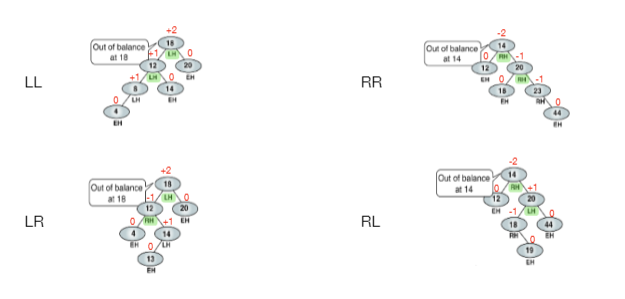
1. LL rotation

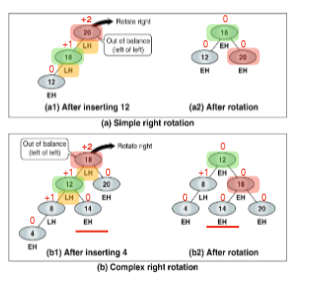
2. LR rotation

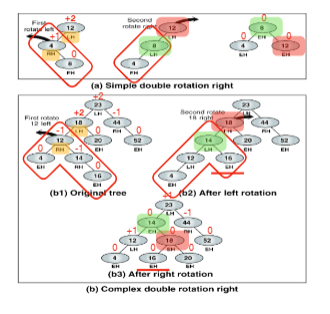
3. RR rotation

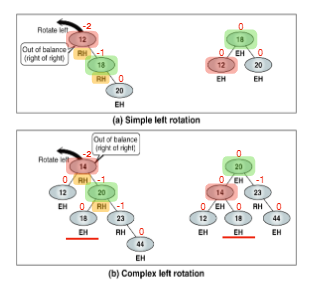
4. RL rotation

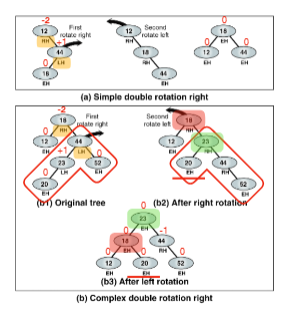
이와 같이 네 가지를 기준으로 적합한 rotation작업을 통해 밸런스를 맞출 수 있게 되는 것이다.

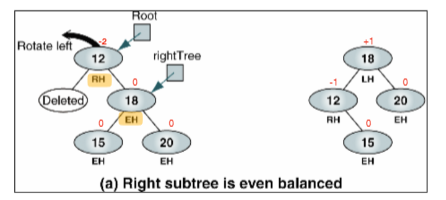
Deletion

그렇다면 마지막으로 deletion을 확인해보자.

이도 마찬가지로 하나를 제거했을 때, 밸런스만 잘 맞추기 위해 rotation을 수행하면 된다.