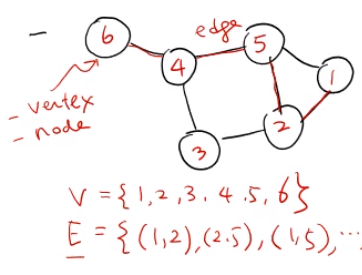
Graph

• 가장 복잡한(일반적인) 자료구조
• G = (V,E) : (vertex set, edge set)
  

자주 등장하는 용어들
Vertex 정점 = node
edge = link
degree 분지수 : 이웃한 노드의 개수
ex) 4의 분지수 = 3, 1의 분지수 = 2, G의 분지수 = 3
인접성 ex) 노드 4와 노드 5는 인접하다(adjacent), edge e = (4,5) : 엣지 e는 노드4와 노드5에 인접하다(incident)
경로 path : 3->2->5 O , 3->2->1->2 X
사이클 cylce : 3->2->5->4->3
Quiz : cycle이 없는 graph는? Tree

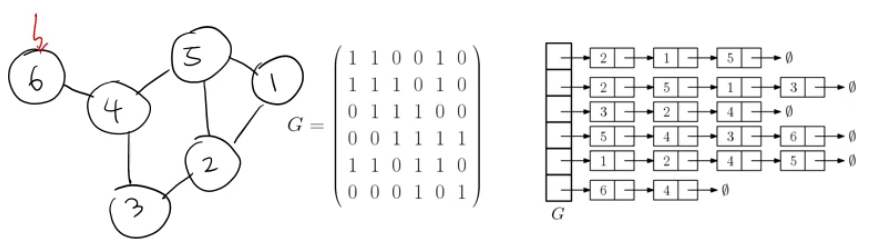
Q. 그렇다면 이러한 인접성들을 어떻게 코드로 표현할 수 있을까?

Graph 표현법
=> 인접성
1) 인접 행렬(adjacent matrix) : 0이 너무 많다. sparse
2) 인접 리스트(adjacent list(연결리스트))

undirected graph 무방향 그래프 : edge에 방향이 없는 그래프
directed graph 방향 그래프 : edge에 방향이 있는 그래프 - 이 때는 원하는 노드로 못 갈 수 있다.

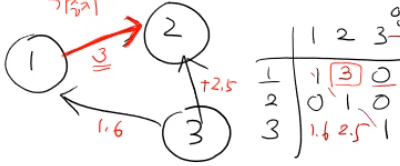
Graph
1) 인접 행렬(adjacent matrix)
2) 인접 리스트(adjacent list(연결리스트))

memory : O(n^2), O(n+m)
(u,v)라는 엣지가 존재하는가? G[u][v] > 1 : O(1), G[u].search(v) : O(n)
u에 인접한 모든 노드 v에 대해 :

for v in range(1,n+1):
	do with G[u][v]
=> O(n)

for each edge in G[u]:
=> O(u와 인접한 노드 개수)

새로운 엣지 (u,v) 삽입 : G[u][v] : O(1), G[u].pushFront(v) : O(1)
(u,v) 삭제 : G[u][v]=0 : O(1), x = G[u].search(v) G[u].remove(x) : O(n)

=> sparse의 경우 인접 리스트, dense한 경우 인접행렬