오늘은 자료구조에 대해 포스팅 해보겠습니다 .
무수한 상황에서 데이터를 효율적으로 다룰 수 있는 방법을 모두 모아, 자료구조라는 이름을 붙였습니다. 우리는 이 많은 방법 중에서, 가장 많이 쓰이고 알고리즘 테스트(코딩 테스트)에 자주 등장하는 네 가지를 학습했습니다 .
Stack

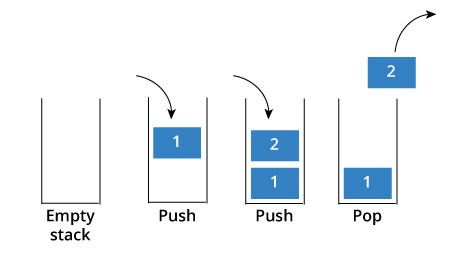
그림을 예로 들어 설명하자면 Stack은 프링글스라고 할 수 있다.
위에 있는 감자칩을 먹어야, 그 아래 있는 감자칩을 먹을 수 있고,
감자칩을 통 속에 넣을 때는 중간에 끼워 넣을 수 없다.
그렇게 쌓아가는 게(stack) 스택이다.
스택에서 사용하는 용어
- top : 데이터가 입출력되는 위치,
( top의 데이터가 0인 상태를 bottom이라고 한다. ) - .push : 입력, top의 위치에 데이터를 입력하고, top을 증가시킨다.
- .pop : 출력 및 삭제, top을 감소시키고, 해당위치의 데이터를 삭제한다.
Stack의 수도코드
스택 생성{
비어있는 top;
비어있는 size;
}
스택.push(data){
data를 top에 입력;
top++;
}
스택.pop(){
top에 있는 데이터 return;
데이터 삭제 후;
top--;
}Stack 코드의 응용
var Stack = function(){ // make Stack
this.top = null;
this.size = 0;
};
var Node = function(data){ // status of data now
this.data = data;
this.previous = null;
};
Stack.prototype.push = function(data) { // push for insert data
var node = new Node(data); // make new node(data)
node.previous = this.top;
this.top = node;
this.size += 1;
return this.top;
};
Stack.prototype.pop = function() { // pop for delete data
temp = this.top;
this.top = this.top.previous;
this.size -= 1;
return temp;
};Queue
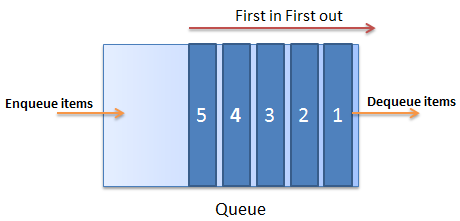
queue 는 줄 이라는 뜻입니다 줄을 세운다는 뜻으로 기본적으로 먼저 입력된것이 먼저 나가는 선입 선출의 방식으로 됩니다.
스택과 달리 큐는 입구와 출구가 구분되어 있기 때문에, 입구로 들어온 데이터는 반드시 반대쪽 출구로 나가야만 합니다.
속성
- first : 큐 맨 앞의 아이템
메소드 - enqueue : 큐에 아이템을 추가한다
- dequeue : 큐 맨 앞의 아이템을 제거하고 및 그 아이템을 반환한다
- contains : 해당 아이템이 큐에 존재하는지 확인한다
- size : 현재 큐에 있는 아이템의 총 개수를 반환한다
메소드 구현해보기
class Stack {
constructor() {
this.top = null;
}
makeNode(value) {
return {
value,
below: null,
};
}
push(...values) {
for (let value of values) {
const node = this.makeNode(value);
if (this.top === null) {
this.top = node;
} else {
node.below = this.top;
this.top = node;
}
}
}
pop() {
if (this.size() === 0) return;
let popped;
if (this.top && this.top.below) {
popped = this.top;
this.top = this.top.below;
} else {
popped = this.top;
this.top = null;
}
return popped.value;
}
contains(value) {
let clone = this.top;
while (clone !== null) {
if (clone.value === value) {
return true;
}
clone = clone.below;
}
return false;
}
size() {
let count = 0;
let clone = this.top;
while (clone !== null) {
count += 1;
clone = clone.below;
}
return count;
}
}Stack 으로 Queue 구현하기
2개의 스택을 이용해 계량컵에 옮기듯 아이템들을 이동시켜 큐를 구현하는 방법이다. 이미 구현한 Stack을 통해 아이템을 추가(enqueue) 하기 위해 메인으로 사용할 스택(inbox)과 삭제(dequeue) 하기 위해 서브로 사용할 스택(outbox)을 만들어 사용한다.
class Queue {
constructor() {
this.inbox = new Stack();
this.outbox = new Stack();
}
enqueue(value) {
this.inbox.push(value);
}
dequeue() {
const size = this.inbox.size();
let temp_size = size;
while (temp_size > 0) {
this.outbox.push(this.inbox.pop());
temp_size -= 1;
}
const dequeued = this.outbox.pop();
temp_size = size - 1;
while (temp_size > 0) {
this.inbox.push(this.outbox.pop());
temp_size -= 1;
}
return dequeued;
}
contains(value) {
return this.inbox.contains(value);
}
size() {
return this.inbox.size();
}
}Tree
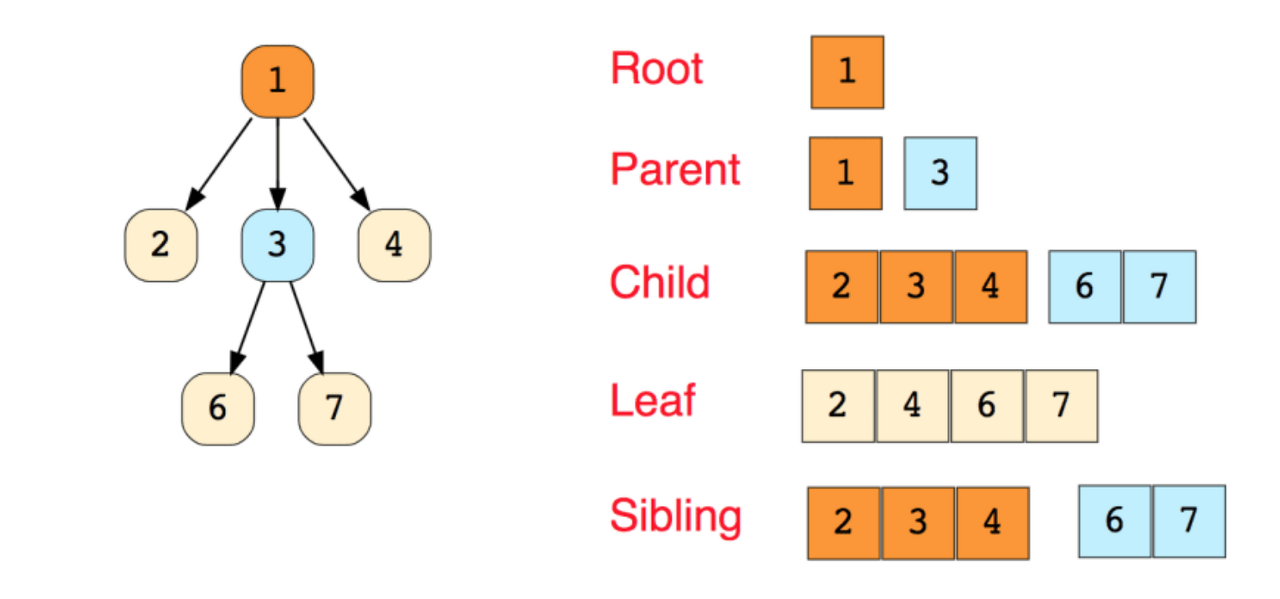
일반적 트리구조
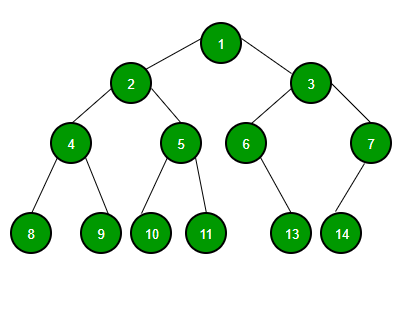
바이너리 트리 구조
Binary Search Tree의 규칙
-
현재 노드의 오른쪽에 있는 노드는 반드시 현재 노드보다 큰 값을 가지고 있다. 반대로 왼쪽에 있는 노드는 현재 노드보다 작은 값이다.
-
각 노드는 최대 2개의 노드만 가질 수 있다.(Binary)
- 장점 : searching, lookup에 아주 빠르다. 예를 들어 37이란 숫자를 찾고자 할 경우, 37이 root보다 작으므로 왼쪽으로 가고, 33보단 크므로 오른쪽으로 가게 되는데, 이 방식을 취함으로써 모든 노드를 iterating 하지 않고도 특정 값을 빠르게 찾을 수 있다. 배열에서 찾는다고 생각해보면, 모든 요소를 iterating하기 때문에 worst 케이스에서 O(n)이 될 수 밖에 없다.
insert와 delete의 경우, 마찬가지로 현재 노드보다 큰지 작은지를 기반으로 삭제/추가 해야 하는 값의 위치로 이동하게 된다. 그런데 만약 위 그림에서 105를 지우면, 이 자리를 대체할 값을 찾아야 하고 144가 105의 자리를 대체하게 된다. 만약 노드의 level이 아주 깊다고 할 경우에는 하단의 모든 level의 값을 하나씩 위로 올려야 하기 때문에 해쉬 테이블에서 값을 삭제할 때의 시간복잡도 O(1)보다 느릴 수 밖에 없다.
이진트리구조
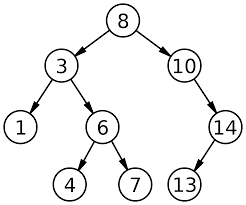
이진 검색 트리는 위와 같이 생겼습니다. 잘 보시면 숫자가 정렬된 것을 알 수 있습니다. 가장 작은 숫자는 가장 왼쪽에, 가장 큰 숫자는 가장 오른쪽에 있습니다
완전 트리 구조
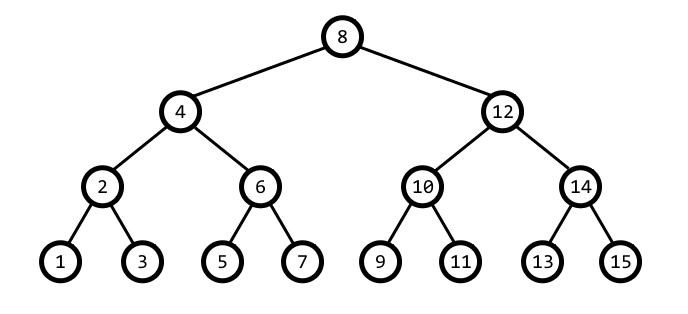
트리 구조 만들기
class CreatTree {
constructor() {
this.matrix = [];
}
addVertex() {
const currentLength = this.matrix.length;
for (let i = 0; i < currentLength; i++) {
this.matrix[i].push(0);
}
this.matrix.push(new Array(currentLength + 1).fill(0));
}
contains(vertex) {
return !!this.matrix[vertex]
}
addEdge(from, to) {
const currentLength = this.matrix.length - 1;
if (from === undefined || to === undefined) {
return;
}
/
if (
from > currentLength ||
to > currentLength ||
from < 0 ||
to < 0
) {
return;
}
this.matrix[from][to] = 1;
}
hasEdge(from, to) {
return !!this.matrix[from][to]
}
removeEdge(from, to) {
const currentLength = this.matrix.length -1;
if (from === undefined || to === undefined) {
return;
}
if (
from > currentLength ||
to > currentLength ||
from < 0 ||
to < 0
) {
return;
}
//TODO: 간선을 지워야 합니다.
this.matrix[from][to] = 0
}
}Graph
그래프 란?
그래프는 상하위의 개념이 없이 각각의 node와 그 node들 간의 간선(edge)을 하나로 모아 놓은 자료구조이다.
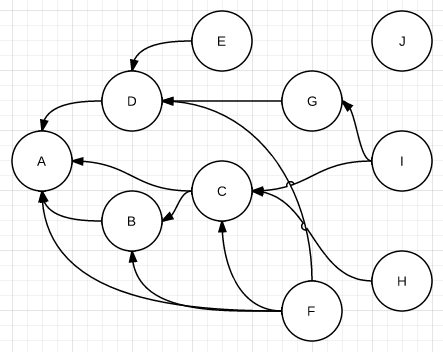
그래프의 특징
그래프는 꼭 모든 node들이 서로 관계를 갖고 있어야만 하지 않다. 따라서 그래프는 node간 연결이 없는 고립된 부분이 있을 수도 있고, 순환할 수도 있고, 안할 수도 있기 때문에 가장 형식에 얽매이지 않은 자료구조라고 볼 수 있다.

그래프 자료구조에서 사용하는 용어
- 노드(node): 위치라는 개념. (vertex 라고도 부름)
- 간선(edge): 위치 간의 관계. 즉, 노드를 연결하는 선 (link, branch 라고도 부름)
인접 노드(adjacent vertex): 간선에 의 해 직접 연결된 노드 - 노드의 차수(degree): 무방향 그래프에서 하나의 노드에 인접한 정점의 수
무방향 그래프에 존재하는 노드의 모든 차수의 합 = 그래프의 간선 수의 2배 - 진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (내차수 라고도 부름)
- 진출 차수(out-degree): 방향 그래픙에서 외부로 향하는 간선의 수 (외차수 라고도 부름)
방향 그래프에 있는 정점의 진입 차수 또는 진출 차수의 합 = 방향 그래프의 간선의 수(내차수 + 외차수) - 경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
- 단순 경로(simple path): 경로 중에서 반복되는 정점이 없는 경우
- 사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
그래프 구조의 수도 코드
새로운 Graph {
그래프 생성자{ 비어있는 노드 리스트 }
노드 생성자 {
노드 이름;
노드와 연결된 노드 리스트[]; //edge
}
노드 입력 {
data = new 노드;
while(edge수){
연결되는 노드에도 edge 추가
}
return graph;
}
}
