[LG Aimer] Convex Optimizer

• 머신러닝 model training = 좋은 parameter set을 찾는것
• 좋은 parameter set = 최적화 문제를 해결

convex

• convex: 볼록하다는 의미
• convex set: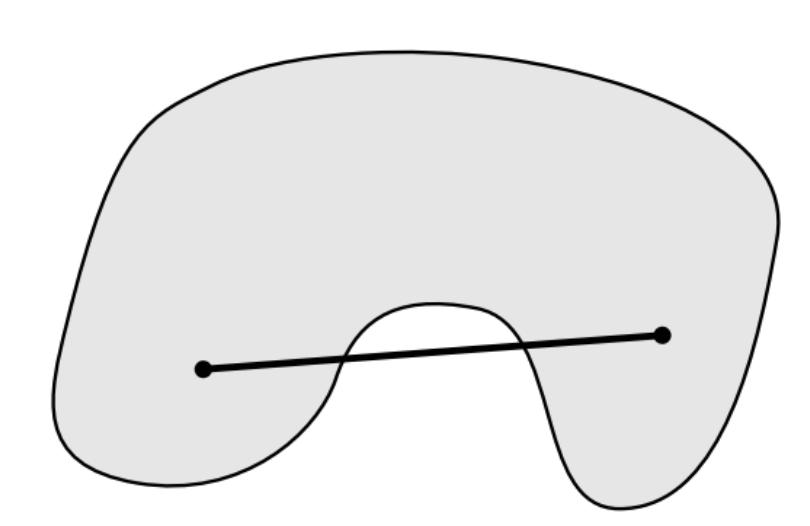
  set 안에 두점 $x_1$,$x_2$를 이은 선분이 set안에 포함될 때 이를 convex set이라 한다
• convex function: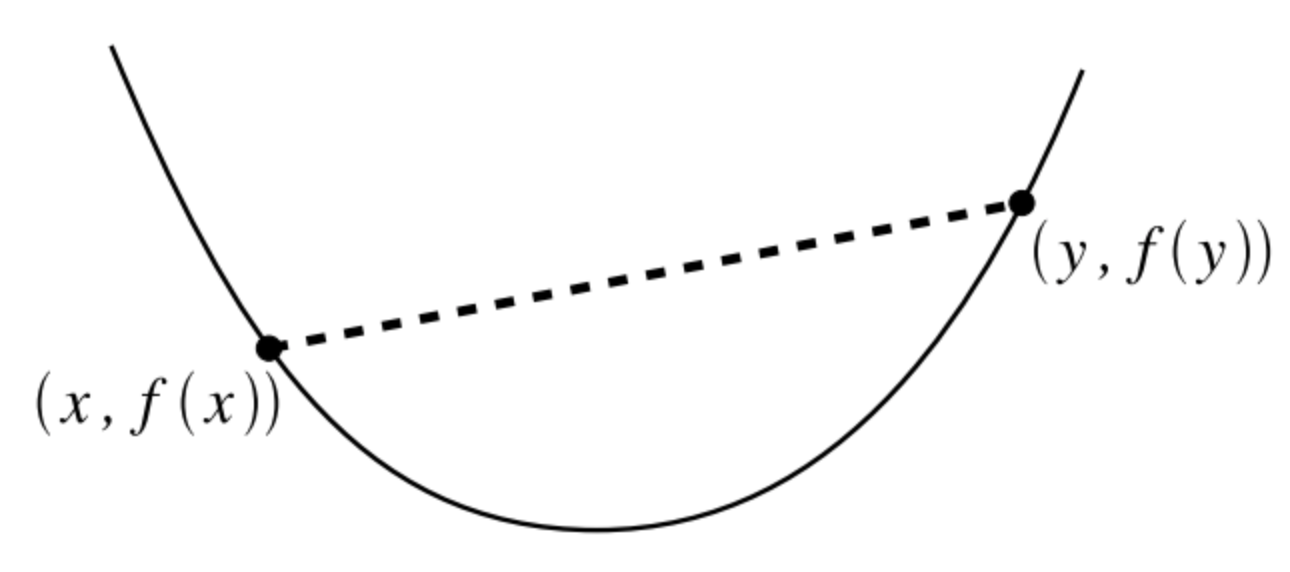
  특정 두 점을 이었을 때 x축을 기준으로 $\theta$라는 비율로 된 곳의 값을 함수 f에 넣은 것이 각각 f(x),f(y)의 같은 비율을 적용한 것보다 작은 값을 가지는 것
  • $f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y)$
  • 1. First Order Condition for Convexity
    • $f(y)-f(x)\geq \nabla f(x)^T(y-x)$
    • f(X)에서의 기울기의 접선은 위의 식처럼 나타난다. 임의의 직선은 f(y)보다 항상 작기 떄문에 $f(y)\geq f(x)$라 하는 데 이것을 First Order Condition for Convexity라 한다
  • 2. Second Order Condition for Convexity
    • 2번 미분할 때 미분값이 0보다 크면 기울기가 증가한다는 뜻.
• concave: convex함수의 반대 방향을 부름

Convex Optimization

$min f(x)$
$subject g_i(x)\leq 0, i=1,2,..,m$

• 수학적 표준 모델
• KTT Condition
  • $L(x,\mu,\lambda) = \nabla f(x)+\sum_{i=1}^{m}\lambda\nabla g_i(x)+\sum_{i=1}^{p}\mu h_i(x) = 0$
  • primal constraints: $g_i(x^*)\leq 0, h_i(x^*)=0$
  • dual constraints: $\mu_i\geq 0$
  • complementray slackness: $\mu_ig_i(x^*)=0$
  • 예제:
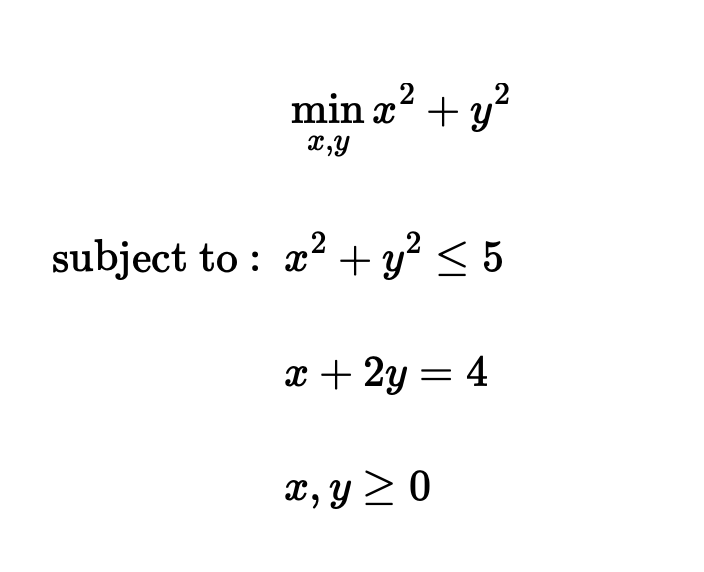
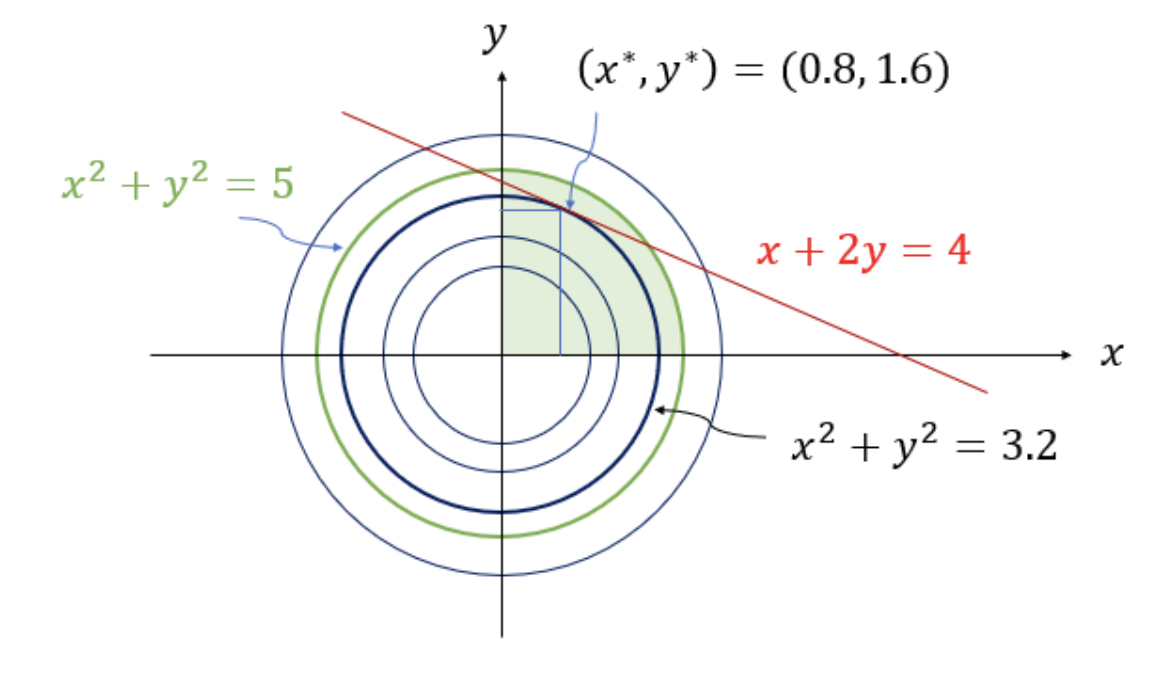
    1사분면의 녹색 영역이 부등식 제약조건이며 빨간색 직선은 등식 제약 조건을 그린 것이다. 녹색 영역안에 있으면서 동시에 빨간색 직선과 접하는 최대 반지름의 제곱이 최적해가 된다.

참고: https://pasus.tistory.com/73