[BOJ 12865] 평범한 배낭

백준 12865번 평범한 배낭 풀러 가기

이번 문제는 DP를 사용하는 대표적인 문제 유형 중 하나인 배낭 문제이다.

배낭 문제에 대한 자세한 설명은 위에 링크를 들어가서 읽어보자.

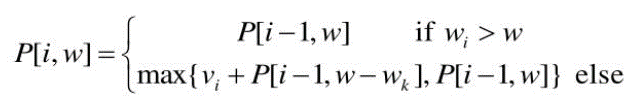
• i번째 짐을 넣었을 때 배낭의 최대 무게를 넘으면, i-1번째까지의 짐을 가지고 구한 최적의 가치가 최대
• i번째 짐을 넣었을 때 배낭의 최대 무게를 넘지 않으면,i-1번째까지의 짐을 가지고 구한 최적의 가치 + i번째 짐의 가치와 i-1번째까지의 짐을 가지고 구한 최적의 가치 중 더 큰 값을 선택

import sys

input = sys.stdin.readline

# 물품의 수, 최대 무게
n, k = map(int, input().split())

dp = [[0 for _ in range(k+1)] for _ in range(n+1)]
weight = [0 for _ in range(101)]
value = [0 for _ in range(101)]

for i in range(n):
    w, v = map(int, input().split())
    weight[i+1] = w
    value[i+1] = v

for i in range(1, n+1):
    for j in range(1, k+1):
    	# i번째 짐을 넣었을 때 배낭의 최대 무게를 넘음
        if j<weight[i]:
            dp[i][j] = dp[i-1][j] # (i-1)번째 짐까지 계산했을 때 최적의 가치
        # 최대 무게를 넘지 않음
        else:
        	# (i-1)번째 짐까지 계산했을 때 최적의 가치와 i번째 짐을 넣었을 때의 가치 중 큰 값
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

print(dp[n][k])