
문제 설명


구현 아이디어
트리도 결국 그래프이기 때문에 그래프 알고리즘을 사용하고자 했다. (사실 트리 관련해서 알고 있는 알고리즘이 ... 없다 🤔)
그래서 플로이드 와샬 알고리즘으로 거리들을 구하고, 그 중 가장 큰 값을 선택하는 방식으로 풀고자 했다.
전체 코드 1 - 메모리 초과
import sys
input = sys.stdin.readline
INF = 1e9
n = int(input())
edges = []
dp = [[INF for _ in range(n+1)] for _ in range(n+1)]
for i in range(1, n+1):
for j in range(1, n+1):
if i == j:
dp[i][j] = 0
for _ in range(n-1):
a, b, c = map(int, input().split()) # 부모 노드, 자식 노드, 가중치
dp[a][b] = c
dp[b][a] = c
for i in range(1, n+1):
for j in range(1, n+1):
for k in range(1, n+1):
dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j])
answer = 0
for elem in dp[1:]:
elem = elem[1:]
answer = max(answer, max(elem))
print(answer)
구현 아이디어 2
구현 아이디어 1이 삼중 반복문을 사용하기 때문에 효율적인 코드가 아니다.
정해를 떠올리지 못할 것 같아 결국 다른 사람의 풀이를 참고하였다.
- 루트에서 가장 먼 노드 n1을 찾는다 (루트 노드는 항상 1번이라고 가정)
- n1에서 가장 먼 노드 n2를 구한다
- n1과 n2의 거리가 트리의 지름이 된다.
해당 풀이를 사용하면, O(N)의 시간 복잡도로 문제를 풀 수 있다.
증명은 구사과 님의 블로그 글을 참고하였다.
🐋 증명
- 루트에서 가장 거리가 먼 점 t가 만약 지름 안에 있다면, 그 점에서 가장 거리가 먼 점인 u까지의 경로가 지름이라는 것은 자명하다.
그러므로 루트에서 가장 거리가 먼 점이 지름 안에 없다는 게 모순임을 보이면 된다. (by 귀류법)
참고) 귀류법 - 어떤 명제가 참이라고 가정한 후, 모순을 이끌어내 그 가정이 거짓임을, 즉 처음의 명제가 거짓임을 증명하는 방법
루트를 1, 루트에서 가장 거리가 먼 임의의 점을 x라 두고 증명해보자.
Case 1
t-u랑1-x랑 겹친다.
둘의 겹치는 부분을 p-q라고 하자.
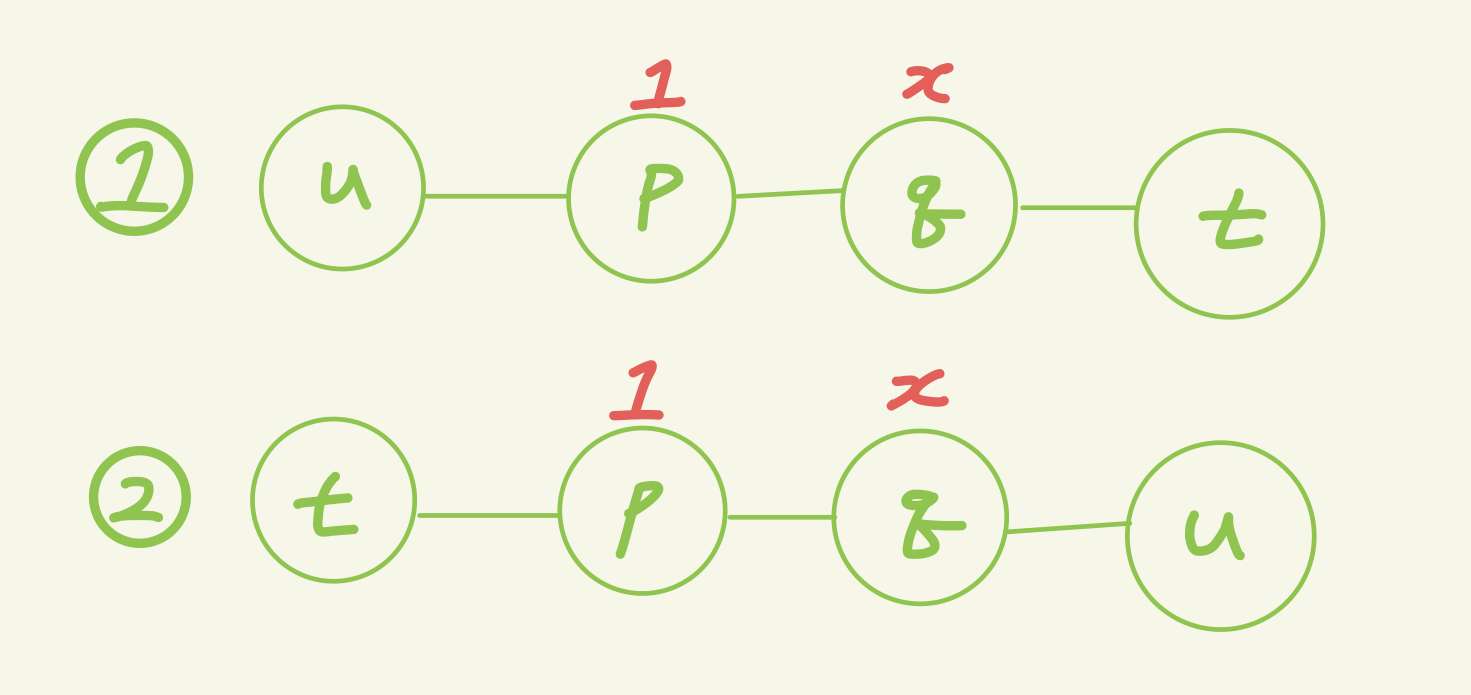
- 첫 번째 경우에서는,
d(1,t)<d(1,x)이다.
그러므로d(q,t)<d(q,x)이고, (위 식에서 1을 q로 치환)
이 때,d(u,t)보다d(u,x)가 길어지므로 u-t는 지름이 아니게 되는 모순이 발생한다.
- 두 번째 경우에서도
d(1,t)<d(1,x)이다.
그러므로d(p,t)<d(p,x)이고, (위 식에서 1을 p로 치환)
d(p,u)<d(p,t)<d(p,x)이므로,d(t,u)보다d(t,x)가 길어져 u-t는 지름이 아니게 되는 모순이 발생한다.
Case 2
t-u랑1-x랑 겹치지 않는다.
1-t와 t-u가 겹치는 점을 p라고 두고, 1-x와 1-t랑 가장 마지막으로 겹치는 점을 q라고 두자.
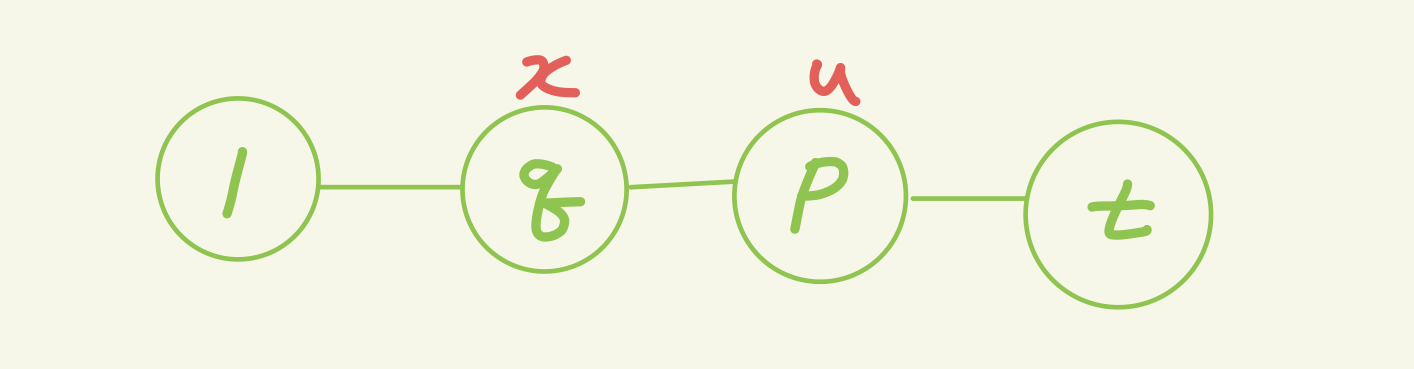
d(p,u) < d(p,t)이며, d(q,t) < d(q,x)이다.
그리고, d(q,u) < d(q,t) < d(q,x)이다.
그러므로 d(t,x) > d(t,q) + d(q,u) > d(t,u) + 2 * d(p,q)이므로 u-t가 지름이 아니게 되어 모순이 발생한다.
전체 코드 2 - 맞았습니다
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**6)
n = int(input())
graph = [[] for _ in range(n+1)] # 인접 리스트
def dfs(x, weight): # 시작 노드, 가중치
for i in graph[x]:
a, b = i # 자식 노드, 가중치
if distance[a] == -1:
distance[a] = weight + b
dfs(a, weight + b)
for _ in range(n-1):
a, b, c = map(int, input().split())
# 무방향 그래프이므로 양쪽 모두에 append
graph[a].append((b, c))
graph[b].append((a, c))
distance = [-1] * (n+1) # 거리를 -1로 초기화
distance[1] = 0 # 1부터 1까지의 거리는 1
dfs(1, 0) # 1을 시작 노드로 하여 DFS 탐색을 진행
n2 = distance.index(max(distance)) # n1에서 가장 거리가 먼 노드
distance = [-1] * (n+1)
distance[n2] = 0
dfs(n2, 0)
print(max(distance))PyPy3 VS Python3
Pypy로 제출하니 메모리 초과가 나왔고, Python3로 제출하니 맞았습니다가 나왔다.
강승현입니다 님의 블로그 글을 참고하여,
pypy3는 가비지 컬렉터가 python3와 다른 구조기 때문에 python3보다 더 많은 메모리로 사용된다는 것을 알 수 있었다.
