프로그래머스 단속카메라 풀러 가기

문제 설명

구현 아이디어 1 - 실패

1. 모든 경우에 대해 겹치는 구간을 찾자
   (단, 탐색 횟수를 줄일 수 있도록 내 뒤에 있는 원소들과만 비교)
2. 겹치는 구간을 저장하자.
3. 다음으로 나오는 겹치는 구간이 2번 구간 안에 있다면, 겹치는 구간을 더 작게 만들자

def solution(routes):
    # 카메라 설치 구간을 저장할 리스트
    cameras = []
    
    # 순서대로 탐색할 수 있도록 진입 지점을 기준으로 정렬
    routes.sort(key= lambda x: x[0])
    
    i = 1 # 내 뒤에 있는 원소들과만 비교할 수 있도록 하는 포인터 변수
    for route in routes:
        for j in range(i, len(routes)):
            current = routes[j]
            # 겹치는 구간이 있다면
            if route[0] <= current[0] <= route[1]:
                # 겹치는 구간을 계산
                intersection = [current[0], min(route[1], current[1])]
                # 이전에 저장한 구간과 겹치는지 확인하여 겹친다면 갱신
                for k in range(0, len(cameras)):
                    if cameras[k][0] <= intersection[0] <= cameras[k][1]:
                        cameras[k] = [intersection[0], min(cameras[k][1], intersection[1])]
                # 겹치지 않는다면 추가
                else:
                    cameras.append(intersection)
        i += 1
    return len(cameras)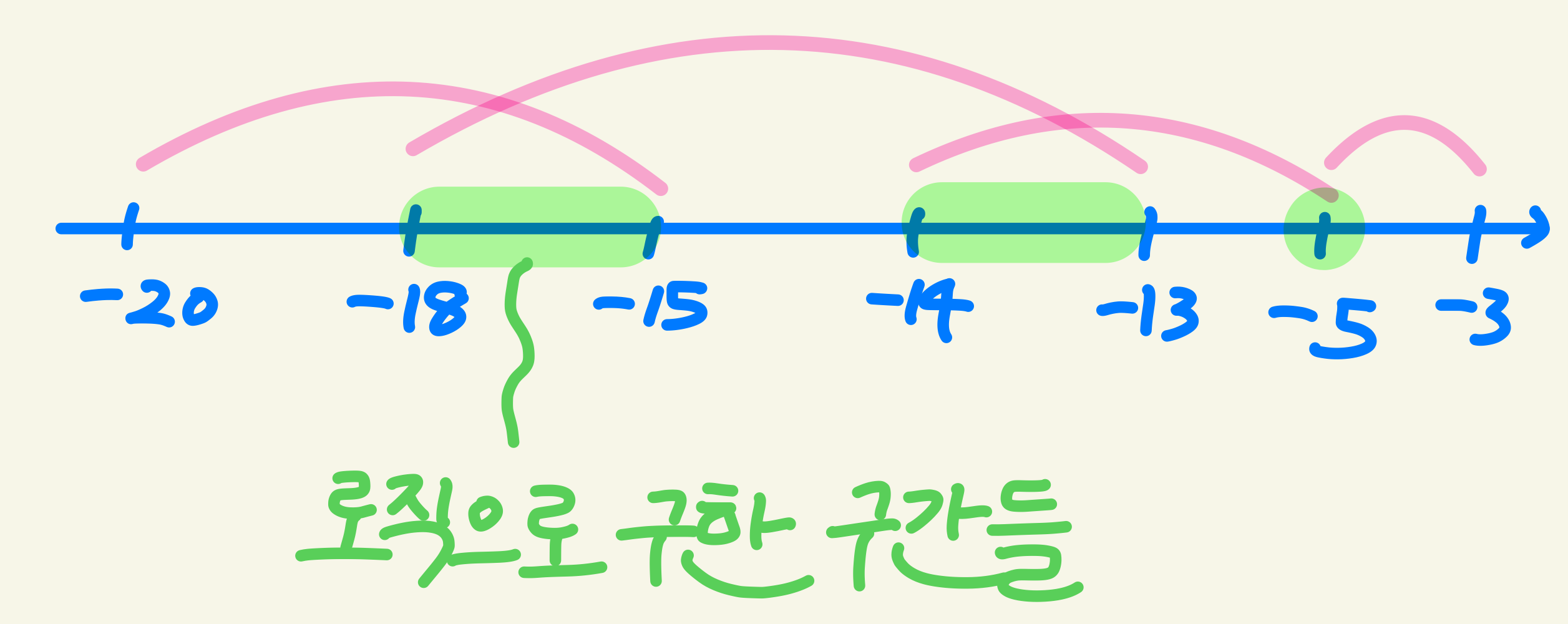

위 로직대로 구간을 구하면 초록색으로 표시한 3가지 구간이 구해진다.
하지만 [-14, -5]가 초록색 구간 2개와 겹치기 때문에 이는 최소가 아니다.

여기까지는 생각을 했지만 ... 겹치는 구간을 없앨 방법이 떠오르지 않아 다른 사람의 코드를 참고하였다.

구현 아이디어 2 - 성공

다른 사람의 코드를 참고한 새로운 구현 아이디어는 아래와 같다

1. 진출 기점을 기준으로 정렬한다.
2. 첫 카메라 위치 = 첫 번째 원소의 진출 지점
3. 반복문을 돌면서
   진입 지점이 현재 카메라 위치보다 뒤 → 카메라 설치 X
   진입 지점이 현재 카메라 위치보다 앞 → 카메라를 현재 원소의 진출 지점으로 갱신

• 진출 기점에 카메라를 설치하는 이유 - 다음 구간의 차량 진입 시점과 비교하면 O(N)으로 확인 가능

def solution(routes):
    answer = 0 # 카메라 개수
    camera = -30001 # 카메라 현재 위치
    
    routes.sort(key= lambda x: x[1]) # 진출 기점을 기준으로 정렬
    # 첫 번째 단속 카메라 설치
    answer += 1
    camera = routes[0][1]
    
    # 단속 카메라가 없는 구간에 카메라 설치
    for i in range(1, len(routes)):
        route = routes[i]
        if route[0] <= camera:
            continue
        answer += 1
        camera = route[1]
    
    return answer

푸는 방법을 알고 나서 푸니 굉장히 쉬운 문제였지만 풀이를 떠올리기 어려운 문제였다.